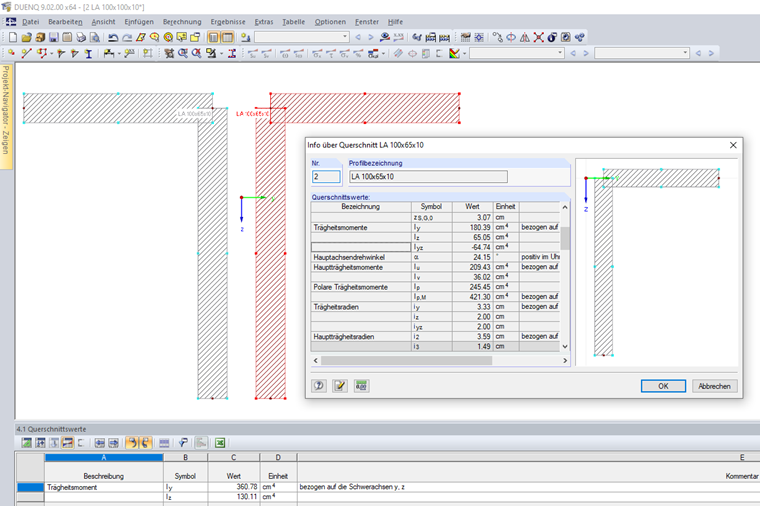
Se la sezione trasversale è composta da più sezioni parziali non collegate , la somma dei momenti di inerzia viene calcolata senza le componenti del teorema degli assi paralleli. La sezione trasversale mostrata nell'immagine 01 è costituita da due sezioni angolari che non sono collegate tra loro.
Le singole sezioni angolari hanno i seguenti momenti di inerzia:
Iy,1,2 = 180,39 cm 4 (riferito agli assi baricentrici y, z)
Iz,1,2 = 65,05 cm 4 (riferito agli assi baricentrici y, z)
I momenti di inerzia dell'intera sezione trasversale risultano in:
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180,39 = 360,78 cm 4 (riferito agli assi baricentrici y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65,05 = 130,11 cm 4 (riferito agli assi baricentrici y, z)
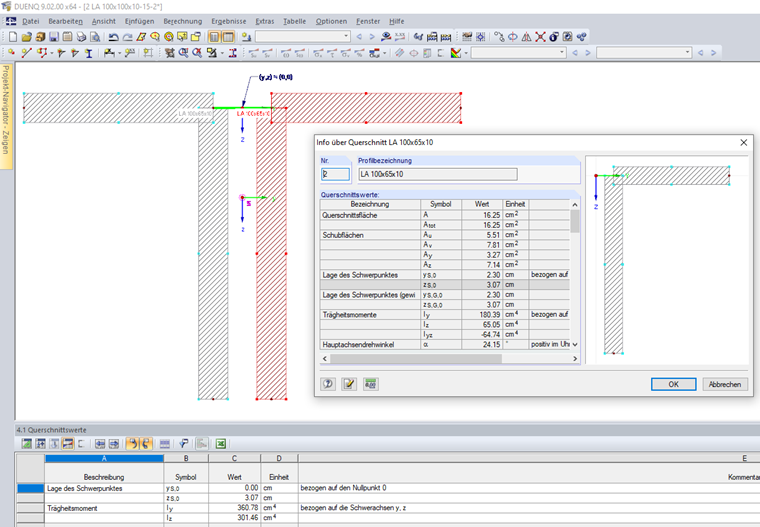
Se la sezione trasversale è composta da più sezioni parziali collegate , la somma dei momenti di inerzia viene calcolata con le componenti del teorema degli assi paralleli. La sezione trasversale mostrata nell'immagine 02 è costituita da due sezioni angolari collegate.
Le singole sezioni angolari hanno le seguenti proprietà della sezione trasversale:
A1,2 = 16,25 cm²
yS,0,1,2 = ±2,30 cm (riferito al punto zero)
zS,0,1,2 = 3,07 cm (riferito al punto zero)
Iy,1,2 = 180,39 cm 4 (riferito agli assi baricentrici y, z)
Iz,1,2 = 65,05 cm 4 (riferito agli assi baricentrici y, z)
Le proprietà della sezione trasversale dell'intera sezione trasversale risultano in:
yS,0,1+2 = 0,00 cm (riferito al punto zero)
zS,0,1+2 = 3,07 cm (riferito al punto zero)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 − zS,0,1+2 ) 2
Iy,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 − 3,07) 2 = 360,78 cm 4 (riferito agli assi baricentrici y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 − yS,0,1+2 ) 2
Iz,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 − 0,00) 2 = 301,46 cm 4 (riferito agli assi baricentrici y, z)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
