Rozdíly ve výpočtu momentů setrvačnosti pro nespojené a spojené dílčí průřezy

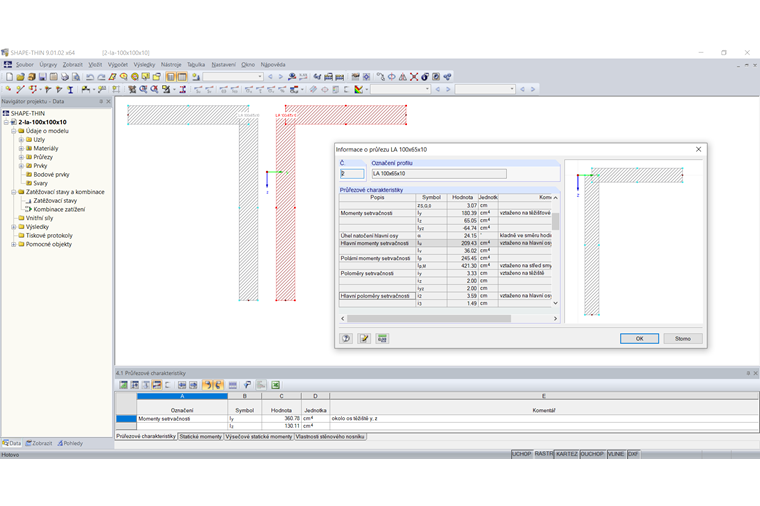
Pokud se průřez skládá z několika nesouvislých dílčích průřezů, počítá se součet momentů setrvačnosti bez složek věty o rovnoběžné osy. Průřez znázorněný na Obrázku 01 se skládá ze dvou navzájem nespojených úhelníků.

1 Průřez z několika nespojených dílčích průřezů

Jednotlivé úhelníky mají následující momenty setrvačnosti:
Iy_{y, 1,2} = 180,39 cm⁴ (vzhledem k těžišťovým osám y, z)
I_z,1,2 = 65,05 cm⁴ (vzhledem k těžišťovým osám y, z)

Momenty setrvačnosti celého průřezu vedou k:
I_y,1+2 = 2 ⋅ I_y,1,2 = 2 ⋅ 180,39 = 360,78 cm ⁴ (vzhledem k těžišťovým osám y, z)
I_z,1+2 = 2 ⋅ I_z,1,2 = 2 ⋅ 65,05 = 130,11 cm⁴ (vzhledem k těžišťovým osám y, z)

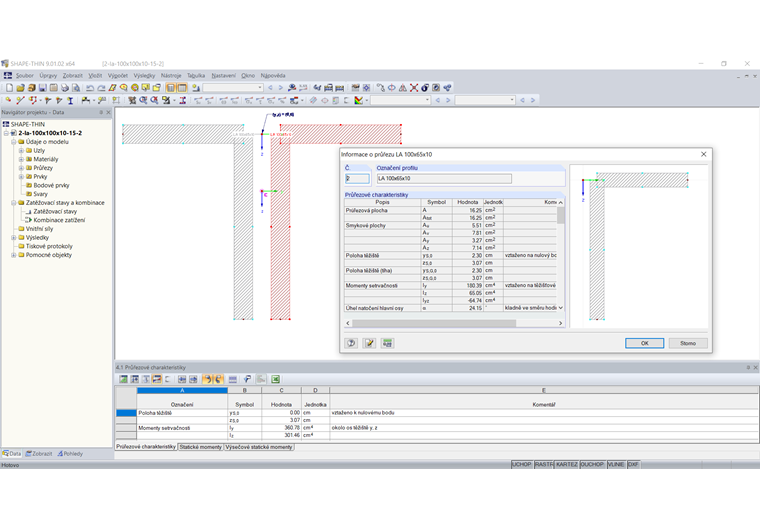
Pokud se průřez skládá z několika spojených dílčích průřezů, počítá se součet momentů setrvačnosti pomocí složek věty o rovnoběžné osy. Průřez znázorněný na Obrázku 02 se skládá ze dvou spojených úhelníků.

2 Průřez z několika spojených dílčích průřezů

Jednotlivé úhelníky mají následující průřezové charakteristiky:
A_1,2 = 16,25 cm²
y_S,0,1,2 = ± 2,30 cm (vzhledem k nulovému bodu)
z_S,0,1,2 = 3,07 cm (vzhledem k nulovému bodu)
Iy_{y, 1,2} = 180,39 cm⁴ (vzhledem k těžišťovým osám y, z)
I_z,1,2 = 65,05 cm⁴ (vzhledem k těžišťovým osám y, z)

Průřezové charakteristiky celého průřezu vedou k:
y_S,0,1+2 = 0,00 cm (vzhledem k nulovému bodu)
z_S,0,1+2 = 3,07 cm (vzhledem k nulovému bodu)
I_y,1+2 = 2 ⋅ I_y,1,2 + 2 ⋅ A_1,2 ⋅ (z_S,0,1,2 - z_S,0,1+2 )²
I_y,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 cm⁴ (vzhledem k těžišťovým osám y, z)
I_z,1+2 = 2 ⋅ I_z,1,2 + 2 ⋅ A_1,2 ⋅ (y_S,0,1,2 - y_S,0,1+2 )²
I_z,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 - 0,00)² = 301,46 cm⁴ (vzhledem k těžišťovým osám y, z)