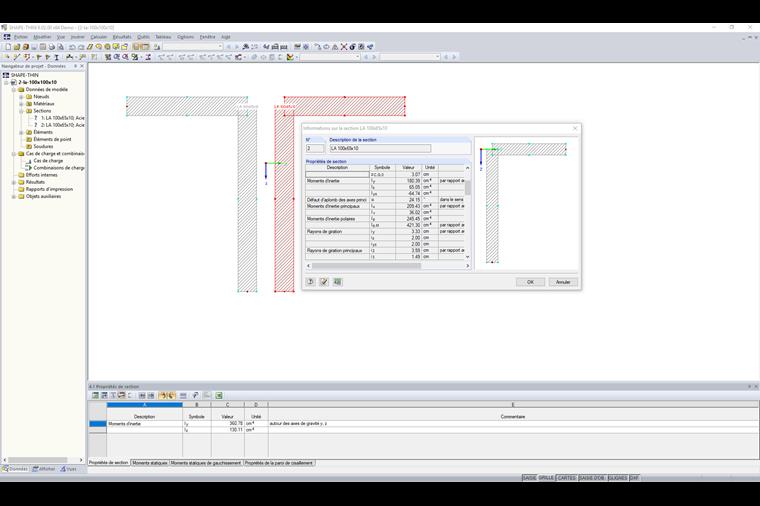
Si la section est constituée de plusieurs composants non connectés , la somme des moments d'inertie est calculée sans les composants du théorème d'axe parallèle. La section représentée sur la Figure 01 se compose de deux sections angulaires non connectées entre elles.
Chaque section angulaire présente les moments d'inertie suivants :
Iy,1,2 = 180,39 cm4 (par rapport aux axes de gravité y, z)
Iz,1,2 = 65,05 cm4 (par rapport aux axes de gravité y, z)
Les moments d'inertie de la section complète sont les suivants :
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180,39 = 360,78 cm 4 (par rapport aux axes de gravité y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65,05 = 130,11 cm4 (par rapport aux axes de gravité y, z)
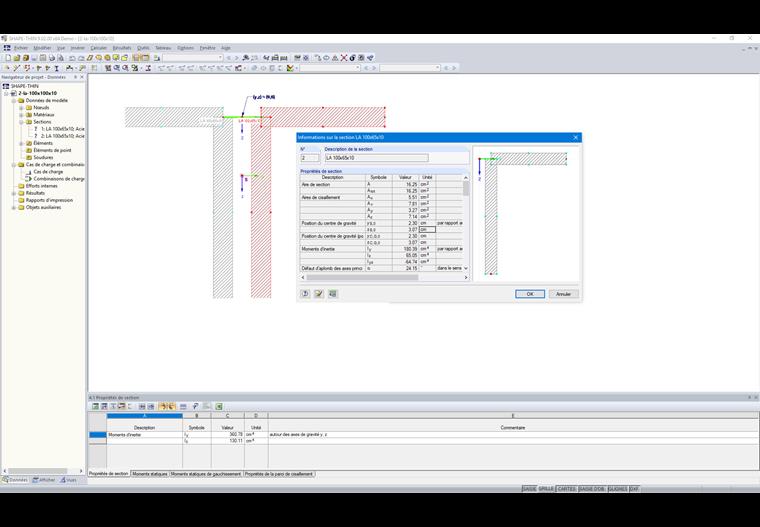
Si la section est constituée de plusieurs composants connectés , la somme des moments d'inertie est calculée avec les composants du théorème d'axe parallèle. La section représentée sur la Figure 02 se compose de deux sections angulaires connectées entre eux.
Chaque section présente les propriétés de section suivantes :
A1,2 = 16,25 cm²
yS,0,1,2 = ±2,30 cm (par rapport au point zéro)
zS,0,1,2 = 3,07 cm (bezogen auf den Nullpunkt)
Iy,1,2 = 180,39 cm4 (par rapport aux axes de gravité y, z)
Iz,1,2 = 65,05 cm4 (par rapport aux axes de gravité y, z)
Les propriétés de la section complète sont les suivantes :
yS,0,1+2 = 0,00 cm (par rapport au point zéro)
zS,0,1+2 = 3,07 cm (par rapport au point zéro)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 - zS,0,1+2 )²
Iy,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 cm4 (autour des axes du centre de gravité y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 - yS,0,1+2 )²
Iz,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 - 0,00)² = 301,46 cm4 (autour des axes du centre de gravité y, z)