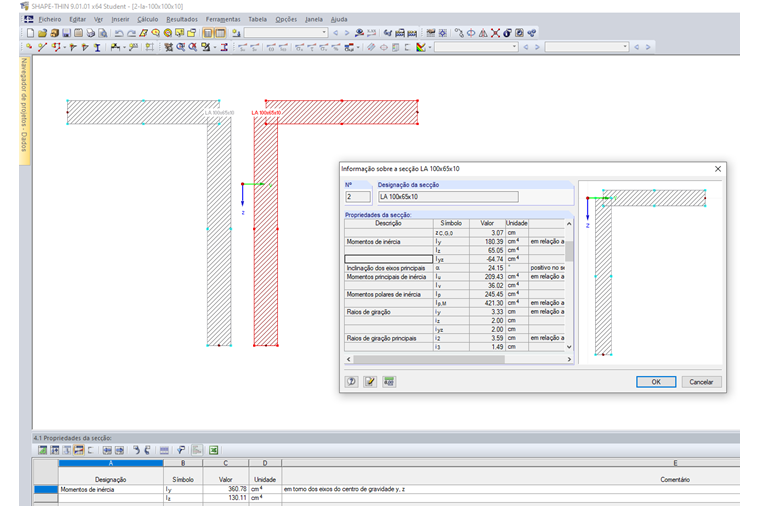
Se a secção for composta por várias secções parciais não ligadas, a soma dos momentos de inércia é calculada sem a parcela do teorema de Steiner. A secção apresentada na Figura 01 é constituída por dois perfis de cantoneira que não estão ligados entre si.
Os perfis de cantoneira individuais têm os seguintes momentos de inércia:
Iy,1,2 =180,39 cm4 (em relação aos eixos do centro de gravidade y, z)
Iz,1,2 = 65,05 cm4 (em relação aos eixos do centro de gravidade y, z)
Os momentos de inércia de toda a secção resultam em:
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180,39 = 360,78 cm4 (em relação aos eixos do centro de gravidade y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65,05 = 130,11 cm4 (em relação aos eixos do centro de gravidade y, z)
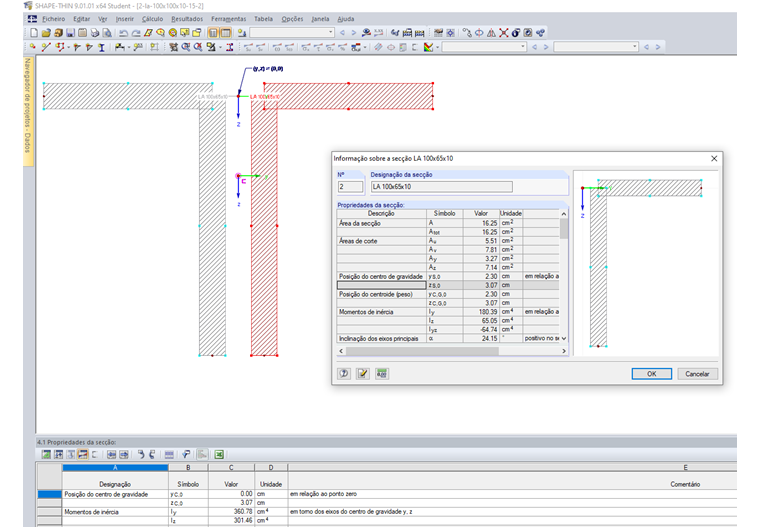
Se a secção for composta por várias secções parciais ligadas , a soma dos momentos de inércia é calculada sem a parcela do teorema de Steiner. A secção apresentada na Figura 02 é constituída por dois perfis de cantoneira que estão ligados entre si.
Os perfis de cantoneira individuais têm as seguintes propriedades de secção:
A1,2 = 16,25 cm²
yS,0,1,2 = ±2,30 cm (em relação ao ponto zero)
zS,0,1,2 = 3,07 cm (bezogen auf den Nullpunkt)
Iy,1,2 =180,39 cm4 (em relação aos eixos do centro de gravidade y, z)
Iz,1,2 = 65,05 cm4 (em relação aos eixos do centro de gravidade y, z)
As propriedades de toda a secção transversal resultam em:
yS,0,1+2 = 0,00 cm (em relação ao ponto zero)
zS,0,1+2 = 3,07 cm (em relação ao ponto zero)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 - zS,0,1+2 )²
Iy,1+2 = 2 ⋅ 180,39 + 2 ⋅ 16,25 ⋅ (3,07 - 3,07)² = 360,78 cm4 (em relação aos eixos do centro de gravidade y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 - yS,0,1+2 )²
Iz,1+2 = 2 ⋅ 65,05 + 2 ⋅ 16,25 ⋅ (2,30 - 0,00) ² = 301,46 cm4 (em relação aos eixos do centro de gravidade y, z)