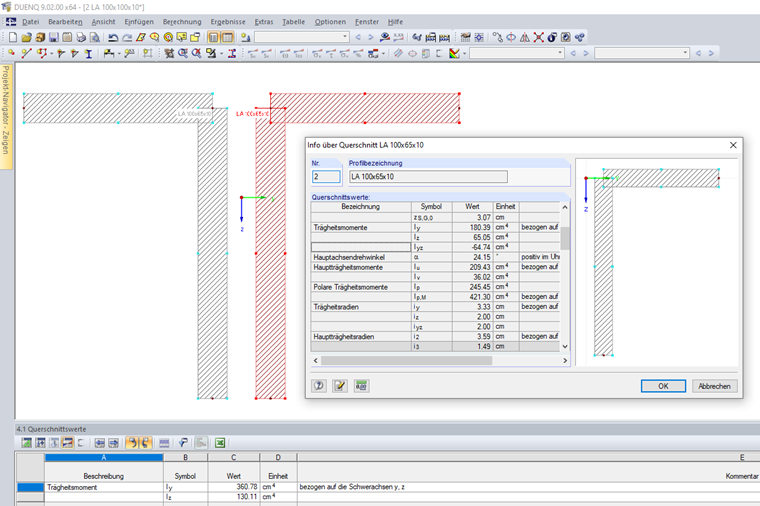
If the cross-section consists of several unconnected partial sections, the sum of the moments of inertia is calculated without the parallel axis theorem components. The cross-section shown in Image 01 consists of two angle sections that are not connected to each other.
The individual angle sections have the following moments of inertia:
Iy,1,2 = 180.39 cm4 (referred to the centroidal axes y, z)
Iz,1,2 = 65.05 cm4 (referred to the centroidal axes y, z)
The moments of inertia of the entire cross-section result in:
Iy,1+2 = 2 ⋅ Iy,1,2 = 2 ⋅ 180.39 = 360.78 cm4 (referred to the centroidal axes y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 = 2 ⋅ 65.05 = 130.11 cm4 (referred to the centroidal axes y, z)
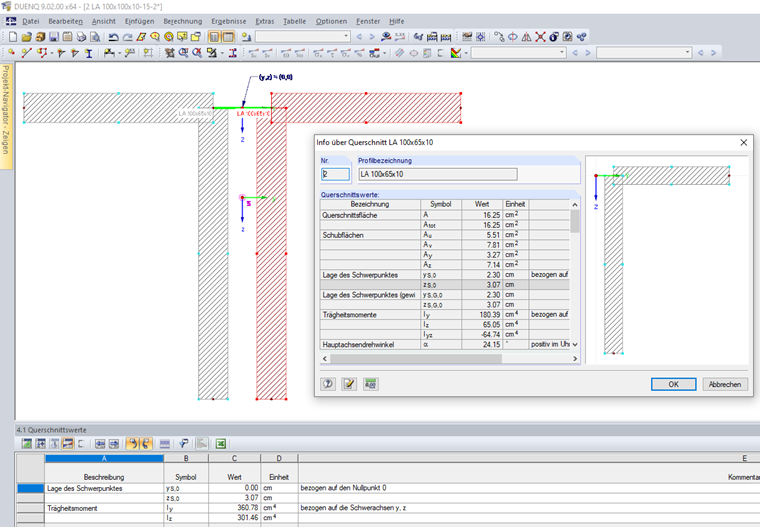
If the cross-section consists of several connected partial sections, the sum of the moments of inertia is calculated with the parallel axis theorem components. The cross-section shown in Image 02 consists of two connected angle sections.
The individual angle sections have the following cross-section properties:
A1,2 = 16.25 cm²
yS,0,1,2 = ±2.30 cm (referred to the zero point)
zS,0,1,2 = 3.07 cm (referred to the zero point)
Iy,1,2 = 180.39 cm4 (referred to the centroidal axes y, z)
Iz,1,2 = 65.05 cm4 (referred to the centroidal axes y, z)
The cross-section properties of the entire cross-section result in:
yS,0,1+2 = 0.00 cm (referred to the zero point)
zS,0,1+2 = 3.07 cm (referred to the zero point)
Iy,1+2 = 2 ⋅ Iy,1,2 + 2 ⋅ A1,2 ⋅ (zS,0,1,2 - zS,0,1+2)²
Iy,1+2 = 2 ⋅ 180.39 + 2 ⋅ 16.25 ⋅ (3.07 - 3.07)² = 360.78 cm4 (referred to the centroidal axes y, z)
Iz,1+2 = 2 ⋅ Iz,1,2 + 2 ⋅ A1,2 ⋅ (yS,0,1,2 - yS,0,1+2)²
Iz,1+2 = 2 ⋅ 65.05 + 2 ⋅ 16.25 ⋅ (2.30 - 0.00)² = 301.46 cm4 (referred to the centroidal axes y, z)