Следующие программы и аддоны особенно подходят для проектов деревянных конструкций.
Основная программа
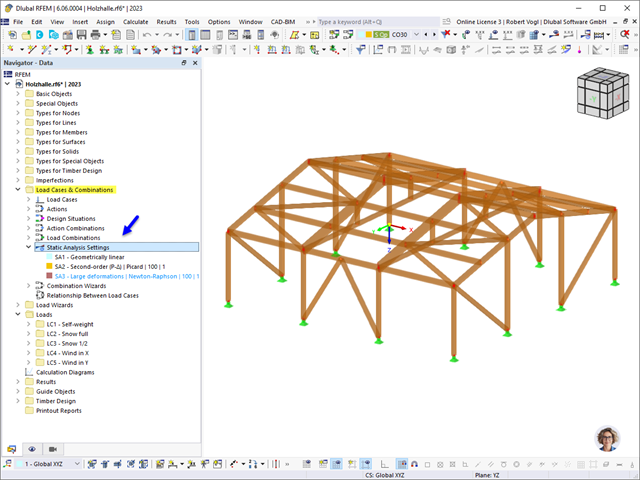
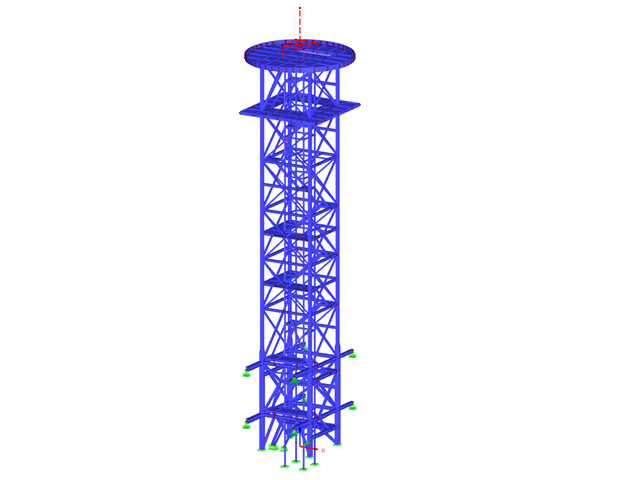
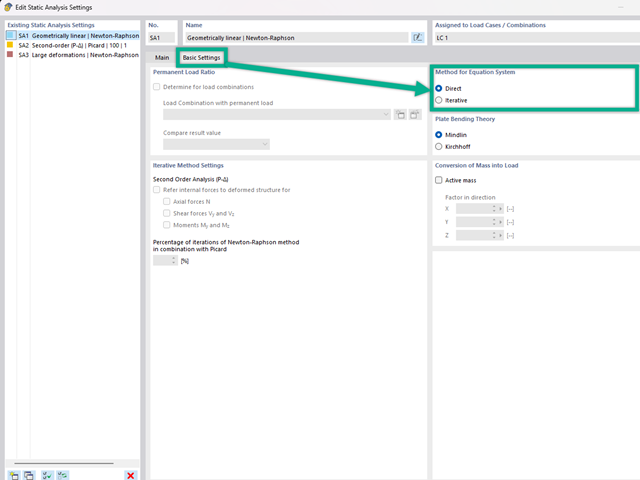
Для моделирования вашей конструкции и определения внутренних сил вам потребуется одна из основных программ. В зависимости от решаемой задачи можно использовать RSTAB 9 или RFEM 6.
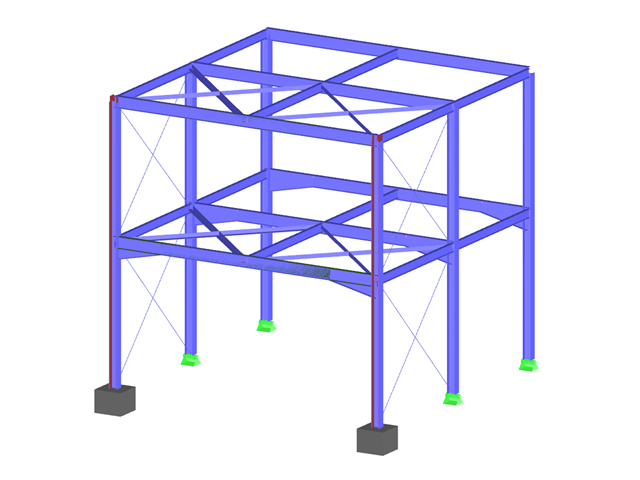
- : Расчёт плоских и пространственных каркасных конструкций
- RFEM: Расчёт по МКЭ конструкций плит, стен, оболочек и стержней
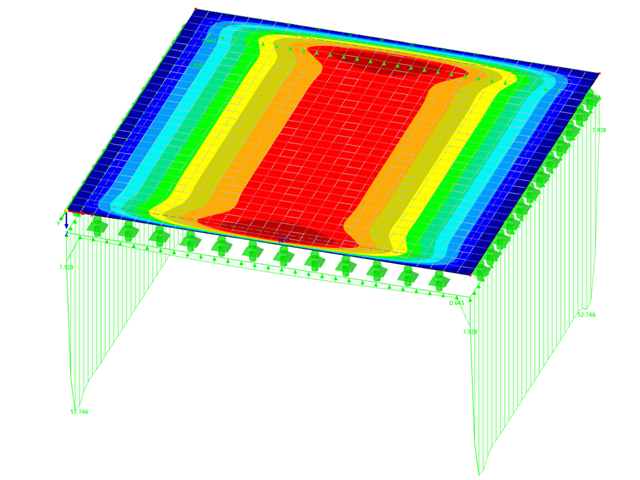
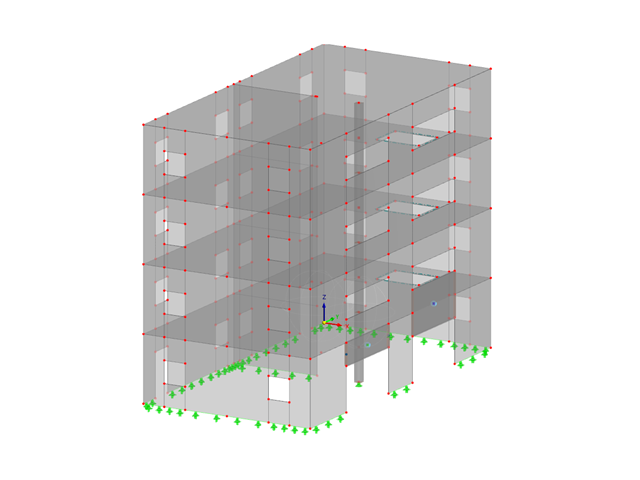
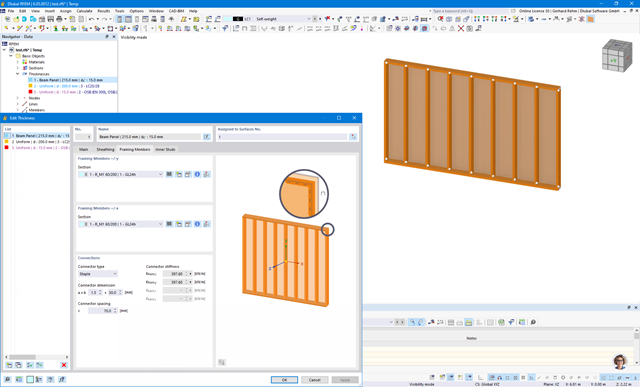
Если ваша модель имеет компоненты поверхности, такие как плиты и стены, в дополнение к элементам стержня, вам понадобится программа RFEM. Уникальные для этой программы опции доступны для расчёта элементов из клееной и кросс-ламинированной древесины, а также криволинейных объектов.
Аддон Расчёт деревянных конструкций
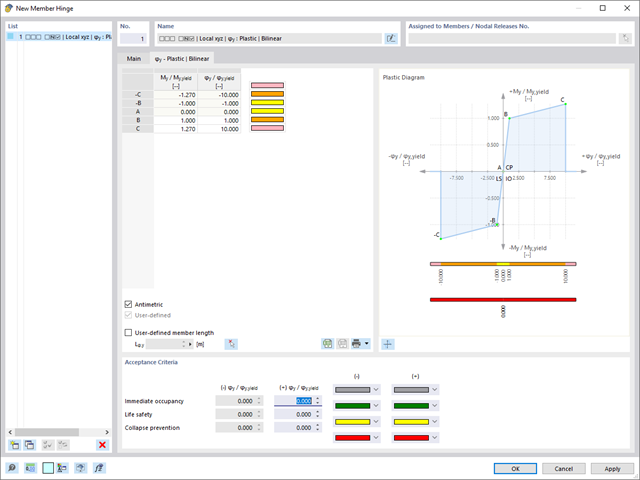
С помощью аддона Расчёт деревянных конструкций на прочность и устойчивость , можно рассчитать деревянные компоненты модели. Специализированные расчеты нормативов охватывают как стержни (изгибаемые балки, колонны), так и поверхности (плиты, стены). Для колонн расчёт на устойчивость выполняется по методу эквивалентного стержня или методу второго порядка.
Расчеты по предельным состояниям по несущей способности и пригодности к эксплуатации, а также расчет на огнестойкость возможны по следующим нормам:
- EN 1995 – включая национальные приложения
- SIA 265
- NTC
- NDS
- CSA O86
- GB 50005
- AS 1720
При расчете на огнестойкость учитывается обгорание сечения 's как для жесткости, так и для расчета.
Аддон Многослойные поверхности
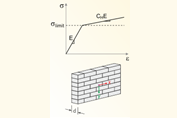
Для программы RFEM доступен аддон Многослойные поверхности , с помощью которого можно рассчитывать ламинированные и многослойные конструкции с пользовательскими композициями слоёв. Благодаря ней можно рассчитывать, например, плиты из поперечно-клеёной древесины.
Если некоторые слои имеют нелинейные свойства материала, вы можете придать им соответствующие свойства. Кроме того, с помощью этого аддона вы также можете анализировать криволинейные поверхности.
Дополнительные аддоны
Для особых требований к деревянной конструкции существуют другие аддоны и программы, которые помогут вам в решении данной задачи.
Если вам нужно выполнить сейсмический расчёт или расчёт колебаний, аддоны для {%>Модальный анализ включается для расчёта собственных частот, а в сочетании с Аддон Расчёт вы также можете выполнить сейсмический расчёт по многочисленным нормативам.
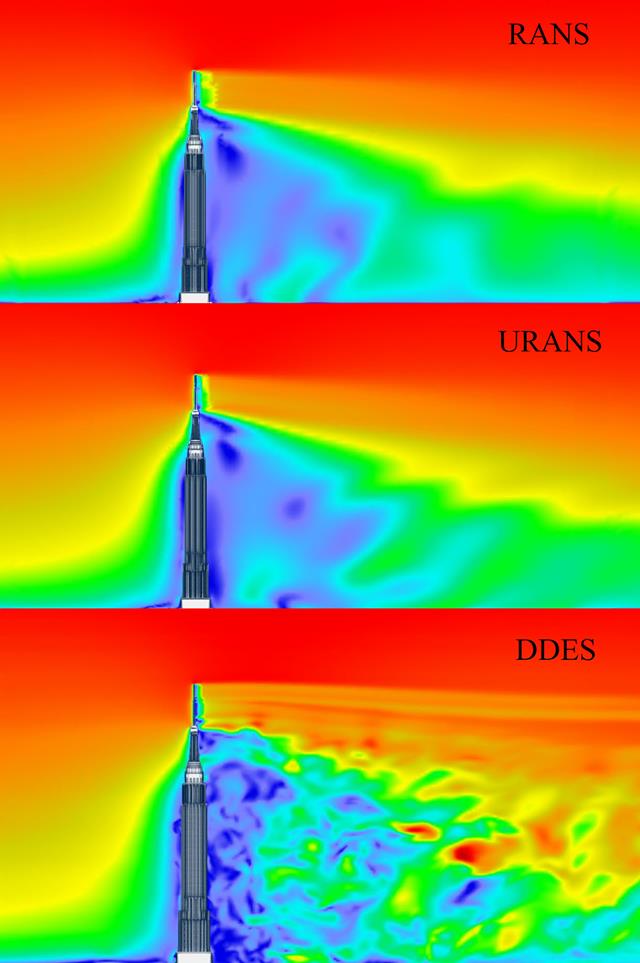
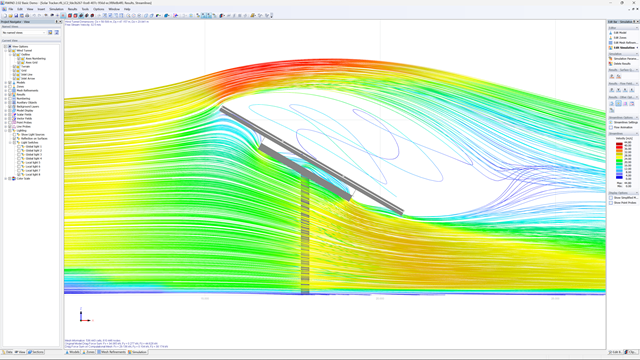
Если вы проектируете здание сложной формы, где определение ветровых нагрузок по соответствующим нормам достигает предела, программа RWIND Программа RWIND поможет вам: С помощью CFD-расчёта можно определить ветровые нагрузки даже для зданий очень сложных форм.
Если стадии строительства влияют на конечные внутренние силы в конструкции или если внутренние силы, определяющие расчет конструкции, возникают на определенных стадиях строительства, тогда следует рассмотреть возможность моделирования с помощью {%://#/ru/produkty/rfem-fea- program/addony-dlja-rfem-6/dopolnitelnye-raschety/raschet-stadij-stroitelstva Аддон Расчёт стадий строительства]]. Аддон Модель здания облегчает ввод большие многоэтажные деревянные конструкции.
Показать больше