介绍
日本建筑协会(AIJ)提供了一些著名的风洞模拟基准工况。
以下是“案例 E – 市区内的建筑群”,该市的建筑群为低层建筑密集的地区。
下面在 RWIND 2 中对所描述的情况进行模拟,并将结果与 AIJ 的模拟结果和实验结果进行比较。
模型布局
工况 E 描述了一个真实的城市区域,该区域的建筑较为密集,但不是很高的建筑物。 只有几座建筑物明显高于其他建筑物。 由于几何形状非常复杂,对几何形状或单个测量点的位置更精确的描述是无关紧要的。 作者将完整的几何图形作为 CAD 文件 [1] 导入到 RFEM 中,以便能够传输到 RWIND 中。
程序的模型布局如下图所示。
在模拟中对明确定义的点的流动速度进行评估。 测量点的确切位置也已在文献 [1] 中公布。
下图显示了测量点的位置。
| x 坐标 | y 坐标 | 点 | x 坐标 | y 坐标 | 点 | x 坐标 | y 坐标 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 112 | 28 | |||||
| 55 | ||||||
| 2 | ||||||
| 33 | 29 | |||||
| 0 | 56 | 38 | 5.5 | |||
| 3 | ||||||
| 35 | 30 | |||||
| 57 | 74 | 22 | ||||
| 4 | ||||||
| 40 | 31 | 6.5 | 52 | 58 | 63 | 0.5 |
| 5 | ||||||
| 45,5 | 32 | 65,5 | 74,5 | 59 | 50.5 | |
| 6 | ||||||
| 49,5 | 33 | 73,5 | 56,5 | 60 | 88.5 | |
| 7 | ||||||
| 57,5 | 34 | |||||
| 61 | 31 | 0 | ||||
| 8 | ||||||
| 69 | 35 | |||||
| 62 | 39.5 | |||||
| 9 | 7 | 76,5 | 36 | |||
| 63 | 92,5 | 20 | ||||
| 10 | 45 | 94 | 37 | |||
| 64 | 100,5 | 3.5 | ||||
| 11 | 80,5 | 110 | 38 | |||
| 65 | ||||||
| 12 | ||||||
| 21 | 39 | |||||
| 66 | ||||||
| 13 | ||||||
| 19 | 40 | 6.5 | 4.5 | 67 | ||
| 14 | ||||||
| 22.5 | 41 | 29.5 | 15 | 68 | 1 | |
| 15 | ||||||
| 29.5 | 42 | 53 | 26 | 69 | 26 | |
| 16 | ||||||
| 36,5 | 43 | 67.5 | 32.5 | 70 | 46.5 | |
| 17 | ||||||
| 47 | 44 | 83 | 39 | 71 | 66.5 | |
| 18 | ||||||
| 56 | 45 | 120,5 | 56,5 | 72 | 82 | |
| 19 | 13,5 | 64,5 | 46 | |||
| 73 | 98.5 | |||||
| 20 | 50 | 81,5 | 47 | |||
| 74 | 56.5 | |||||
| 21 | 87 | 97,5 | 48 | |||
| 75 | 109 | |||||
| 22 | ||||||
| 49 | ||||||
| 76 | 116 | |||||
| 23 | ||||||
| 8 | 50 | |||||
| 77 | 5 | |||||
| 24 | ||||||
| 33 | 51 | |||||
| 78 | 45.5 | |||||
| 25 | ||||||
| 22 | 52 | |||||
| 79 | 81.5 | |||||
| 26 | ||||||
| 11 | 53 | |||||
| 80 | 125 | |||||
| 27 | ||||||
| 16 | 54 | |||||
与具有较低几何复杂性的模型相比,在这种情况下在 RWIND 中创建网格时的详细程度设置非常重要。 如果精细化程度较低(例如默认值 2),则环绕网格可以封闭建筑物或内部庭院之间的小胡同。 因此我们强烈建议将详细程度设置为最大值 4。 下图显示了网格密度为 15% 时的问题。
“网格密度”相同时,划分出的单元数量和质量会大相径庭。 因此,我们建议在所有情况下都使用“详细程度” 4,并且仅在该设置的基础上优化网格密度。
在 AIJ 实验中,我们建立了一个相应的风洞模型,并在上述各点使用剖腹杆测量风速。
作者使用了三种建模方法,在本文中只使用了“代码T”。 选择该模型的原因是它是一种未指定的商业求解器,而不是单独开发的代码,因为它更容易用于特殊目的,并且 RWIND 也是一种商业工具。
为了清楚起见,这里省略了 RWIND 与所有三种建模方法的比较。 此外,出版物 [1] 中不同方法的结果在质量上没有显着差异。 这里展示的对比结果也是与其他两个模型进行比较。
本文使用 RWIND Pro 2.02。 RWIND 中的模型结构尽可能地与参考 CFD 的结构进行了调整。 湍流模型采用标准 k-ε ,假设为稳态流。 这里是参照文献 [1] 中的西风方向进行比较的。 在下面的相对风速比较中,标准风速大于 2.77 m/s。
下方显示了该高度上的气流速度。
| 高度 m | 流动速度 m/s | |
|---|---|---|
| 1 | 1.25 | 2,8470 |
| 2 | 2,50 | 3,0420 |
| 3 | 5,00 | 3,2604 |
| 4 | 7,50 | 3,4086 |
| 5 | 12,50 | 3,7674 |
| 6 | 25,00 | 4,3602 |
| 7 | 50,00 | 5,1090 |
| 8 | 75,00 | 5,6940 |
| 9 | 100,00 | 6,1620 |
| 10 | 150,00 | 6,9654 |
| 11 | 200,00 | 7,3944 |
| 12 | 250,00 | 7,8000 |
AIJ 的实验结果已经发布在他们的网站 [1] 上。
AIJ 模拟显示的数据是使用数字化仪工具 ENGAUGE [2] 从出版物 [1] 中的图形中确定的,因为这里的确切值并未发布。
但是提取点的精度应该足够高(在 +-0.5% 范围内)并且容易进行比较。
另一个重要的影响因素是“边界层”设置,它会显着增加下边界条件(土)周围的网格密度。 一般情况下,贴近地面的网格划分比离地面较远的区域对结果的影响更大,因为地面边界条件的影响更强。 由于城市的几何形状非常复杂,所以激活上述设置并将额外层数(“NL”)设置为 10。
结果与讨论
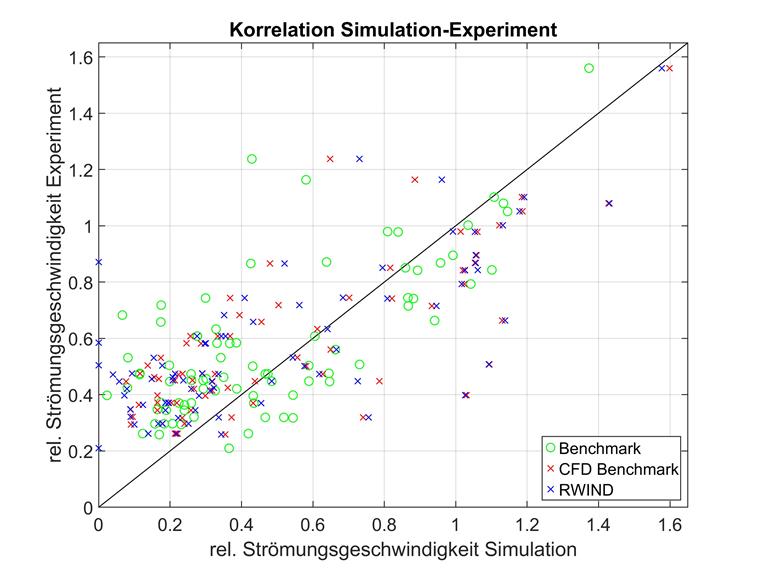
通过简单的一维编号表示三维定位的测量点通常比较难以理解。 下面显示了所有测量点的实验结果(x 轴)和模拟结果(y 轴)的对比图。 测量点越靠近对角线 y=x,模拟和实验之间的相关性就越大。
虽然使用了均方差 (MSD) 进行比较,但在确定系数的比较中也显示出相同的结果。 人们更喜欢均方差而不是决定系数,因为实验风速和模拟出的风速之间的比值不代表回归,而只是对各个偏差的一种权重,而不是拟合的优缺点。 在相同的表现力下,MSD 从几何上更容易理解。
最高建筑物附近的区域特别显眼;也就是在实验中具有最低速度的那些点。 对于这组点,可以观察到 RWIND 和实验之间的相关性高于 RWIND 与美国AIJ模拟之间的相关性. 在后面的详细分析中将对该区域进行更详细的介绍。
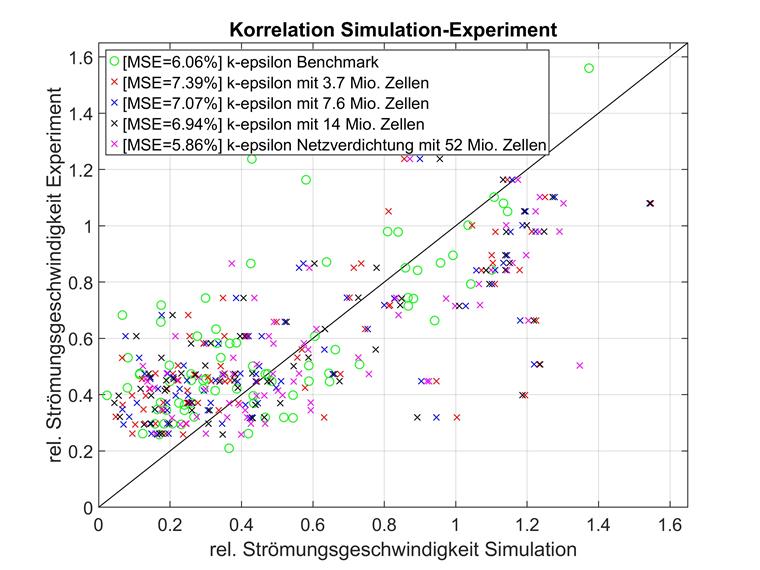
通常仔细观察网格密度的影响。 下面将在相同的模型结构和 RAS 湍流模型中设置不同密度的网格与文献中的基准进行比较。 计算结果如下图所示。
各个数据点位于相对流动速度的范围内,尤其是在 0 和 0.8 之间。 与实验的相关性有时在规定范围以内和外出显着差异。 为了便于比较,在数据中标注了rel。 当速度小于 0.8 倍时,会显示在两个轴上,并相应地重新计算均方差。
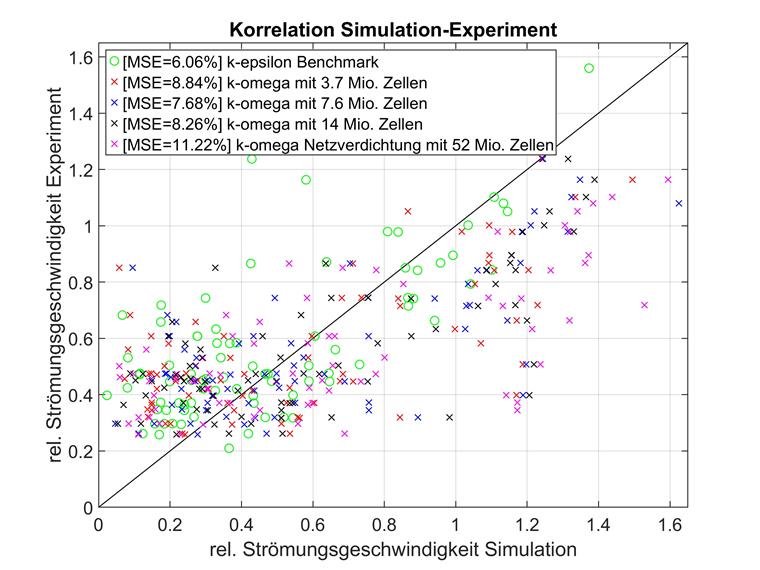
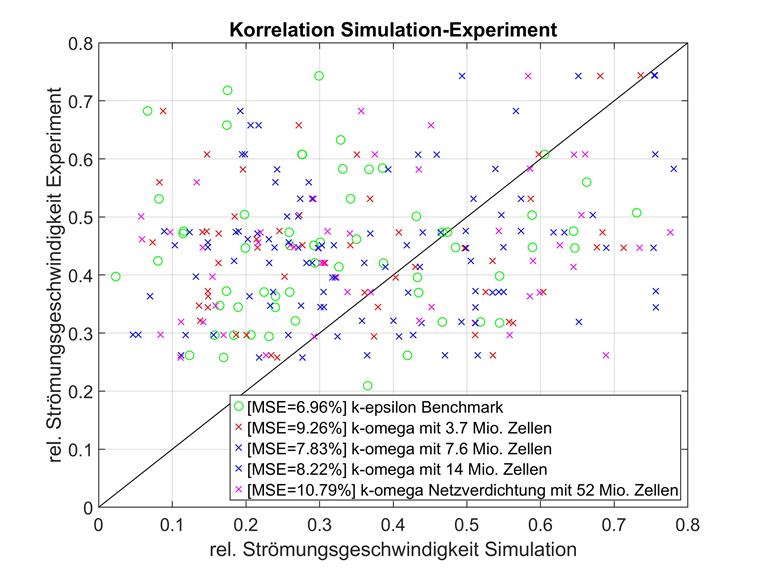
此外,还对 k-omega 湍流模型和相同的网格形成进行了网格收敛性研究。 计算结果如下图所示。
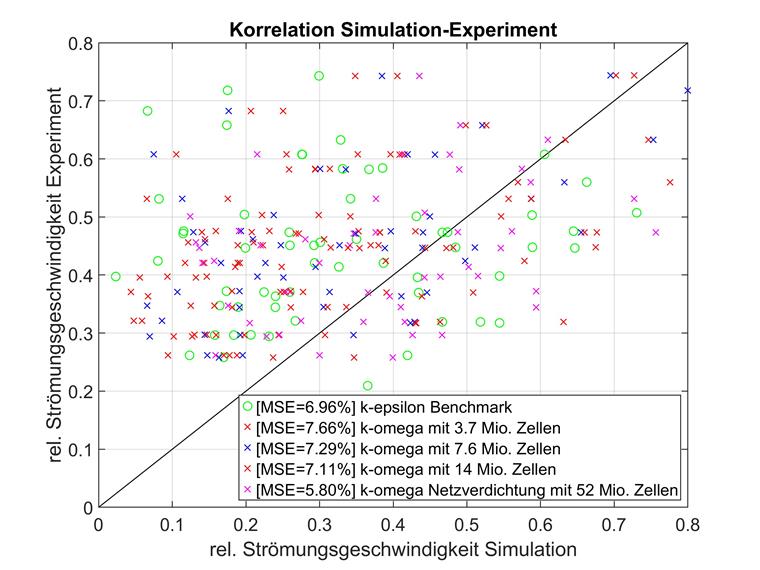
关于比较 k-ε 模型,分别对低流动速度下的 k-ω 进行了比较。 下图显示了计算结果。
在这里要确认通过比较 k-epsilon 模型得出的结果。 对于低分辨率网格,相对流动速度小于 0.8,与实验基准的偏差大于与平均数据点的偏差。
随着单元数量的增加,这种影响会被减小,对于较低的相对流动速度,紧密划分网格的模型偏差甚至更小。
包含在这个单独考虑中的点往往位于建筑物更密集的区域。 因为点的位置可以解释更复杂的网格结果更好,因为越精细的网格可以更准确地表达几何。 因为真实几何形状对这些点的影响大于相对速度大于 0.8 的点,所以网格越密越符合实验。
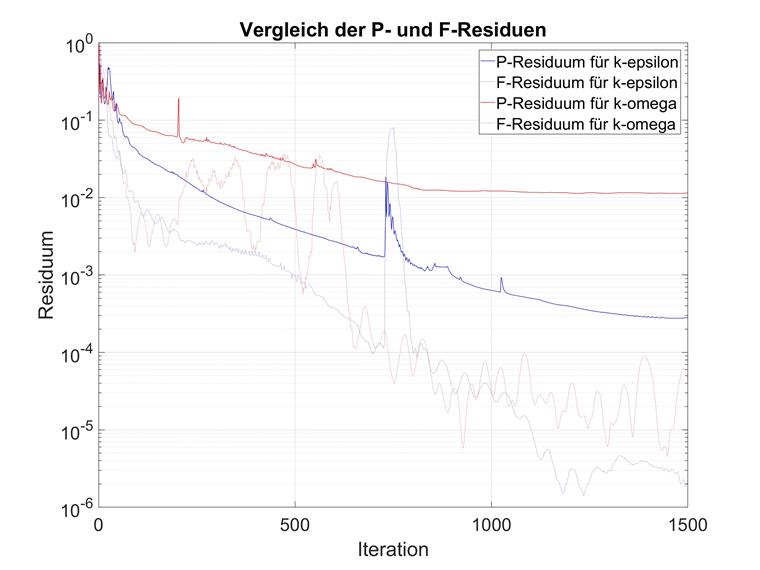
这些观察结果与各种湍流模型的预期相符。 因此,我们建议在使用 k-omega 时显着增加最大迭代次数。 默认值 300 应手动增加到至少 1000。
总而言之,在 RWIND 中两种湍流模型的比较中情况 E 的情况不如情况 D 清楚。 在该示例中,显示了对任意网格密度 k-ε模型的优越性。 此外,随着单元数量的增加,k-epsilon 比 k-omega 更好。 即使网格密度较高,湍流模型的结果也不会出现收敛。 中等复杂度的模型得到最好的结果,而在非常复杂的模型中得到的结果与实验基准的偏差最大。 因此,k-omega 的结果在预期的范围内,并且在更高网格密度的情况下也可以优于参考模拟。 特别是最大的 k-omega 模型会出现很大的偏差。 因此目前还无法确定除了对ε 的影响程度不同外,对欧米伽 k 的影响系数还不能确定。
为了更清楚地比较参考模拟和 RWIND 的结果,建议使用彩色瓶图来查看风速。
所考虑的最高建筑物周围的截面根据作者的选择 [1] 进行了调整。 结果如下所示。
由于版权原因,假彩色图像在这里没有并排进行比较。
此外,在测量点水平上显示了整个城市的气流速度的假彩色图像。
与文献模拟计算也有很好的相关性。 较小的偏差主要出现在建筑物的拐角处,但范围很小,并且影响范围非常有限。
概述总结
当单元编号和湍流模型的不同组合时,其均方差如下所列:
| k-epsilon 湍流模型 | k-omega 湍流模型 | |
|---|---|---|
| 参考 | 6.06% | 不适用 |
| 370 万个单元 | 7.39% | 8.84% |
| 760 万个单元格 | 7.07% | 7.68% |
| 1400万个单元 | 6.94% | 8.26% |
| 5200 万个单元 | 5.86% | 11.22% |
下面对不同的速度范围进行比较。
| k-ε小于 0.8 | k-epsilon (大于 0.8) | k-omega 小于 0.8 | k-omega超过 0.8 | |
|---|---|---|---|---|
| 参考 | 6.96% | 1.52% | 不适用 | 不适用 |
| 370 万个单元 | 7.66% | 6.09% | 9.26% | 6.83% |
| 760 万个单元格 | 7.29% | 5.96% | 7.83% | 6.99% |
| 1400万个单元 | 7.11% | 6.07% | 8.22% | 8.42% |
| 5200 万个单元 | 5.80% | 6.12% | 10.79% | 13.53% |
[1]
城市风环境 CFD 预测指南
[2]
Engauge 数字化仪


.png?mw=760&hash=d578a909f5296e100ae606d6ae168d70a1c0ca37)