Présentation
L'Institut d'architecture du Japon (AIJ) a présenté un certain nombre de scénarios de référence bien connus pour la simulation des flux de vent.
L'article suivant traite du « Cas E - Complexe de bâtiments dans la zone urbaine réelle avec une concentration dense de bâtiments peu élevés dans la ville de Niigata ».
Le scénario décrit est simulé dans RWIND 2 et les résultats sont comparés aux résultats simulés et initiaux de l'AIJ.
Disposition du modèle
Le cas E décrit une section de ville réaliste avec un développement dense, mais des bâtiments peu élevés. Seuls quelques bâtiments se démarquent nettement des autres. Une description plus précise de la géométrie ou de la position des différents points de mesure n'est pas pertinente en raison de la géométrie très complexe. La géométrie complète a été mise à disposition par les autrices sous forme de fichier CAO [1] et importée dans RFEM pour cet article afin de pouvoir la transférer dans RWIND.
La disposition du modèle est illustrée ci-dessous.
La vitesse du flux a été évaluée dans la simulation à des points clairement définis. La position exacte des points de mesure a également été publiée [1].
La position des points de mesure est indiquée ci-dessous.
| Coordonnée-x | Coordonnée-y | Point | Coordonnée-x | Coordonnée-y | Point | Coordonnée-x | Coordonnée-y | |
|---|---|---|---|---|---|---|---|---|
| 1 | -27 | 112 | 28 | -39.5 | -4 | 55 | -11 | -50 |
| 2 | -93 | 33 | 29 | -32 | 0 | 56 | 38 | 5.5 |
| 3 | -88 | 35 | 30 | -39 | -11 | 57 | 74 | 22 |
| 4 | -74 | 40 | 31 | 6.5 | 52 | 58 | 63 | 0,5 |
| 5 | -61 | 45,5 | 32 | 65,5 | 74,5 | 59 | 50.5 | -22.5 |
| 6 | -50.5 | 49,5 | 33 | 73,5 | 56,5 | 60 | 88.5 | -6 |
| 7 | -33.5 | 57,5 | 34 | -117.5 | -32 | 61 | 31 | 0 |
| 8 | -9.5 | 69 | 35 | -86.5 | -35.5 | 62 | 39.5 | -20 |
| 9 | 7 | 76,5 | 36 | -75 | -31.5 | 63 | 92,5 | 20 |
| 10 | 45 | 94 | 37 | -55.5 | -23 | 64 | 100,5 | 3,5 |
| 11 | 80,5 | 110 | 38 | -26 | -10 | 65 | -83 | -94 |
| 12 | -133 | 21 | 39 | -9 | -2,5 | 66 | -49.5 | -78.5 |
| 13 | -97 | 19 | 40 | 6.5 | 4.5 | 67 | -10 | -59.5 |
| 14 | -84 | 22,5 | 41 | 29.5 | 15 | 68 | 1 | -54 |
| 15 | -65.5 | 29.5 | 42 | 53 | 26 | 69 | 26 | -43 |
| 16 | -47.5 | 36,5 | 43 | 67.5 | 32.5 | 70 | 46.5 | -33.5 |
| 17 | -25 | 47 | 44 | 83 | 39 | 71 | 66.5 | -24.5 |
| 18 | -5 | 56 | 45 | 120,5 | 56,5 | 72 | 82 | -17.5 |
| 19 | 13.5 | 64,5 | 46 | -121 | -56.5 | 73 | 98.5 | -9.5 |
| 20 | 50 | 81,5 | 47 | -96.5 | -59.5 | 74 | 56.5 | -54.5 |
| 21 | 87 | 97,5 | 48 | -77 | -59 | 75 | 109 | -17.5 |
| 22 | -114.5 | -8 | 49 | -59.5 | -51.5 | 76 | 116 | -30.5 |
| 23 | -90.5 | 8 | 50 | -45.5 | -45 | 77 | 5 | -94 |
| 24 | -56 | 33 | 51 | -24.5 | -19.5 | 78 | 45.5 | -86.5 |
| 25 | -51 | 22 | 52 | -31 | -23.5 | 79 | 81.5 | -69.5 |
| 26 | -46.5 | 11 | 53 | -24.5 | -38 | 80 | 125 | -49.5 |
| 27 | -39 | 16 | 54 | -20 | -30.5 |
Contrairement aux modèles moins complexes géométriquement, le réglage du niveau de détail lors de la création du maillage dans RWIND est très pertinent dans ce cas. Pour un niveau de détail faible, tel que la valeur par défaut 2, le maillage de thermorétraction ferme les allées entre les bâtiments ou les cours intérieures. Par conséquent, nous vous recommandons fortement de définir le niveau de détail à la valeur maximale de 4. Voici le problème avec une densité de maillage de 15 %.
Malgré le même paramètre en ce qui concerne la densité du maillage, le nombre d'éléments et donc de qualité du maillage sont très différents. Il est donc recommandé d'utiliser le niveau de détail 4 dans tous les cas et d'optimiser la densité de maillage uniquement à partir de ce paramètre.
Dans l'expérience AIJ, un modèle correspondant a été construit dans une soufflerie et la vitesse du vent a été mesurée aux points mentionnés à l'aide de relevés à fibre divisée.
Les autrices ont utilisé trois approches de modélisation, dont seul le « Code T » est utilisé dans cet article. Ce modèle a été sélectionné car il s'agit d'un solveur commercial non spécifié, au lieu d'un code développé individuellement qui serait plus facile à appliquer à des fins spéciales, et parce que RWIND est également un outil commercial.
La comparaison de RWIND avec les trois approches de modélisation a été omise pour des raisons de clarté. De plus, les résultats des différentes approches de la publication [1] ne diffèrent pas beaucoup en termes de qualité. Les comparaisons présentées ici sont donc très similaires avec les deux autres modèles.
RWIND Pro 2.02 a été utilisé pour cet article. La structure du modèle dans RWIND était adaptée aussi étroitement que possible à la structure de la CFD de référence. La norme k–ε a été utilisée comme modèle de turbulence en supposant un flux stationnaire. Les comparaisons effectuées ici se rapportent à la direction ouest du vent dans la publication [1]. Pour les comparaisons suivantes de la vitesse relative du vent, elle a été normalisée sur 2,77 m/s.
La vitesse du flux sur la hauteur est indiquée ci-dessous.
| Hauteur en m | Vitesse du flux en m/s | |
|---|---|---|
| 1 | 1,25 | 2,8470 |
| 2 | 2.50 | 3,0420 |
| 3 | 5,00 | 3,2604 |
| 4 | 7,50 | 3,4086 |
| 5 | 12,50 | 3,7674 |
| 6 | 25,00 | 4,3602 |
| 7 | 50,00 | 5,1090 |
| 8 | 75,00 | 5,6940 |
| 9 | 100,00 | 6,1620 |
| 10 | 150,00 | 6,9654 |
| 11 | 200,00 | 7,3944 |
| 12 | 250,00 | 7,8000 |
Les résultats structuraux de l'AIJ ont été publiés sur son site Web [1].
Les données affichées de la simulation AIJ ont été déterminées à l'aide du numériseur ENGAUGE [2] à partir des tracés de la publication [1], car les valeurs exactes de celui-ci n'ont pas été publiées.
La précision des points extraits doit cependant être suffisamment précise (dans l'intervalle +-0,5 %).
Le paramètre « Couches de contour », qui augmente considérablement la densité du maillage autour de la condition de contour inférieure (sol), constitue un autre facteur d'influence. En général, le maillage près du sol influence les résultats dans cette région plus que ce ne serait le cas à une plus grande distance du sol, car la condition aux limites du sol a une forte influence. En raison de la géométrie très complexe de la ville, le paramètre mentionné ci-dessus a été activé et le nombre de couches supplémentaires (« NL ») défini sur 10.
Résultats et analyse
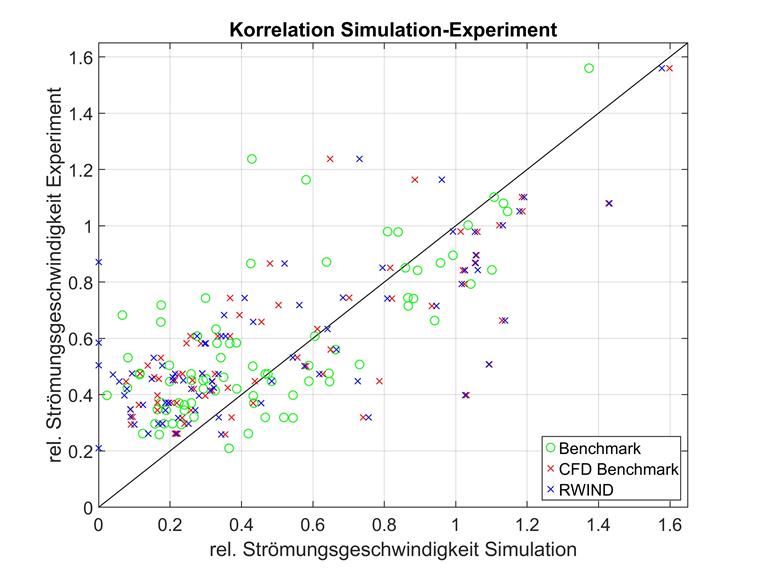
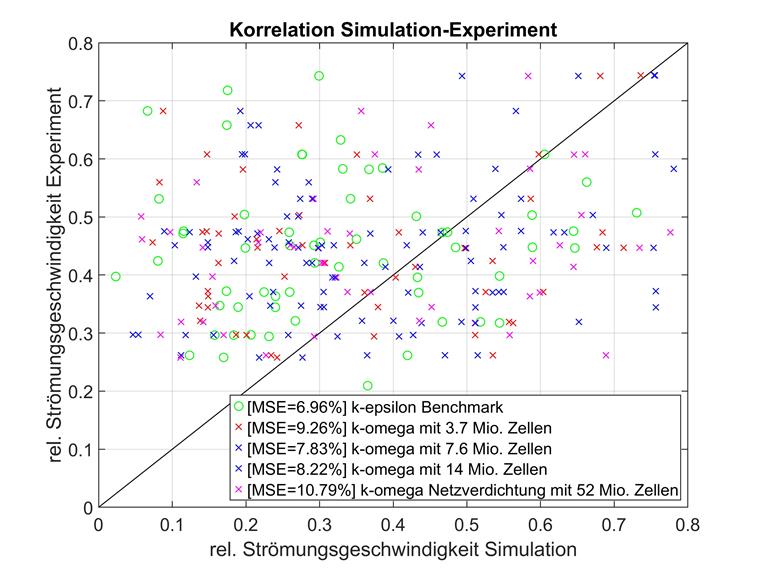
La représentation des points de mesure positionnés en trois dimensions par une simple numérotation unidimensionnelle peut être difficile à interpréter. Par conséquent, des comparaisons directes de l'expérience (axe x) et de la simulation (axe y) sont présentées ci-dessous pour tous les points de mesure. Plus un point de mesure est proche de la diagonale y = x, plus la corrélation entre la simulation et l'expérience est grande.
La déviation quadratique moyenne (MSD) a été utilisée comme critère de comparaison, mais la comparaison des coefficients de détermination montrerait également le même comportement, par exemple. L'écart carré moyen a été préféré au coefficient de détermination car le rapport de la vitesse d'écoulement expérimentale et simulée ne représente pas une compression et ne serait donc qu'une sorte de pondération des écarts individuels et non un ajustement correct. Le MSD est géométriquement plus facile à interpréter avec la même expression.
La région proche du bâtiment le plus haut se distingue par une attention particulière ; c'est-à-dire les points avec la vitesse d'écoulement la plus faible dans l'expérience. Pour ce groupe de points, un degré de corrélation plus élevé peut être observé entre RWIND et l'expérience qu'entre RWIND et la simulation AIJ. Cette région sera examinée plus en détail dans l'analyse détaillée ultérieure.
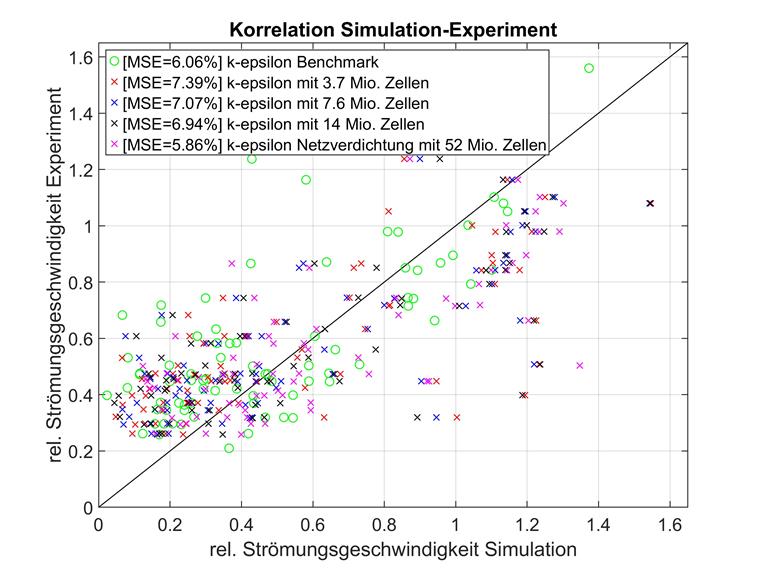
Il est généralement recommandé de regarder de plus près l'influence de la densité du maillage. Des maillages de différentes densités avec une structure par ailleurs identique et un modèle de turbulence k-epsilon RAS sont comparés à la référence de la littérature spécialisée. Les résultats se trouvent dans les tableauc ci-dessous.
Les points de données individuels se situent dans la plage de la vitesse d'écoulement relative, en particulier entre 0 et 0,8. La corrélation avec les expériences diffère parfois considérablement à l'intérieur et à l'extérieur de la plage indiquée. Par souci de comparaison, seuls les points de données avec rel. les vitesses d'écoulement inférieures à 0,8 sont affichées pour les deux axes et les écarts carrés moyens sont recalculés en conséquence.
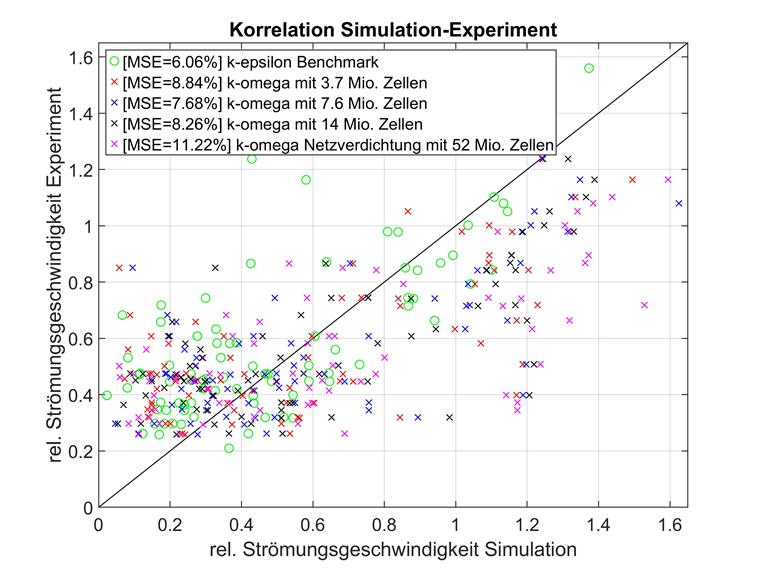
Une étude de convergence du maillage a également été réalisée pour le modèle de turbulence k-omega et les mêmes formations de maillage. Les résultats se trouvent dans les tableauc ci-dessous.
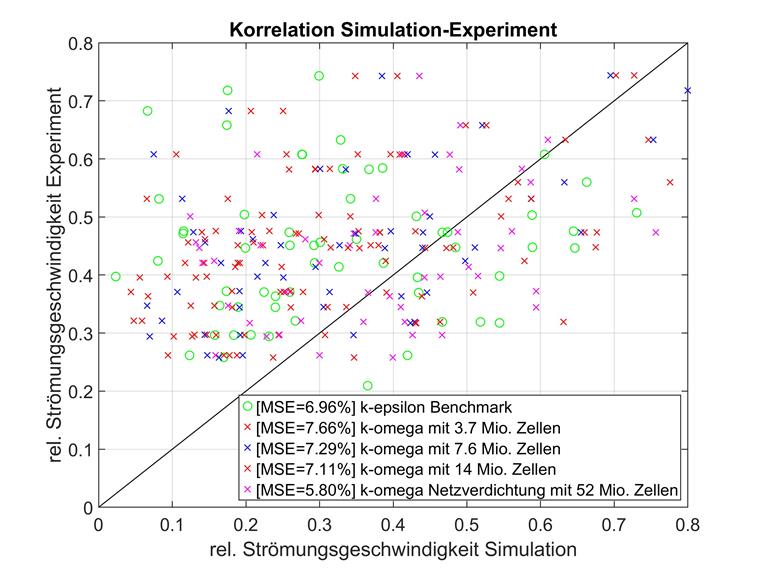
Tout comme lors de la comparaison des modèles k-epsilon, les faibles vitesses d'écoulement ont été comparées séparément pour k-omega. Ces données sont visualisées ci-dessous.
Les résultats de la comparaison des modèles k-epsilon sont confirmés ici. Pour les maillages à résolution inférieure, les vitesses d'écoulement relatives inférieures à 0,8 s'écartent plus de la référence expérimentale que des points de données globaux moyens.
Cependant, avec un nombre croissant d'éléments, cet effet s'inverse, de sorte que les modèles à maillage étroit s'écartent encore plus pour les faibles vitesses d'écoulement relatives.
Les points inclus dans cette considération distincte ont tendance à être situés dans des zones plus denses. La position des points pourrait expliquer les meilleurs résultats des maillages plus complexes, car les maillages plus fins peuvent représenter la géométrie avec plus de précision. Étant donné que la géométrie réelle influence ces points plus que les points avec des vitesses d'écoulement relatives supérieures à 0,8, le maillage plus dense convient mieux à l'expérience.
Ces remarques coïncident avec les attentes des différents modèles de turbulence. Pour l'utilisation de k-omega, il est donc recommandé d'augmenter considérablement le nombre d'itérations maximum. La valeur par défaut de 300 doit être augmentée manuellement jusqu'à au moins 1 000.
Pour conclure, la comparaison des deux modèles de turbulence dans RWIND est par exemple moins claire pour le cas E que pour le cas D. Dans cet exemple de référence, le modèle k-epsilon est supérieur pour toute densité de maillage. De plus, k-epsilon est bien plus nombreux que k-omega car le nombre d'éléments augmente. Les résultats de ce dernier modèle de turbulence ne semblent pas suivre de convergence avec une densité de maillage plus élevée. Le modèle de complexité moyenne donne les meilleurs résultats, tandis que le modèle très complexe affiche le plus grand écart de loin par rapport à la référence expérimentale. Ainsi, les résultats de k-epsilon se situent dans la plage souhaitée et peuvent également dépasser la simulation de référence si la densité de maillage est élevée, mais aucune conclusion congruente ne peut être tirée pour k-omega. L'écart très élevé pour le plus grand modèle k-omega en particulier est un Cas particulier. Il n'a sans doute pas été possible d'identifier un facteur déterminant de k-omega, mais qui n’affecte pas de la même manière k-epsilon.
Pour comparer plus clairement la simulation de référence avec les résultats de RWIND, il est conseillé d'afficher les vitesses du flux sous forme d'image en couleur.
La section considérée autour du bâtiment le plus haut a été adaptée à celle des autrices [1]. Le résultat est affiché ci-dessous.
Pour des raisons de droit d'auteur, les images en fausses couleurs ne sont pas comparées à ce stade.
De plus, l'image en fausses couleurs de la vitesse du flux sur l'ensemble de la ville a été affichée au niveau des points de mesure.
Il existe également une très bonne corrélation avec la simulation de la littérature. Les petits écarts se produisent principalement aux coins du bâtiment avec un flux important, mais ils sont de petite taille et sont très limités dans l'espace.
Conclusion
Les écarts quadratiques moyens des différentes combinaisons du numéro d'élément et du modèle de turbulence sont résumés ci-dessous.
| Modèle de turbulence k-epsilon | Modèle de turbulence k-omega | |
|---|---|---|
| Ouvrage spécialisé | 6,06 % | non applicable |
| 3,7 millions de cellules | 7,39 % | 8,84 % |
| 7,6 millions de cellules | 7,07 % | 7,68 % |
| 14 millions de cellules | 6,94 % | 8,26 % |
| 52 millions de cellules | 5,86 % | 11,22 % |
Les différentes plages de vitesse sont comparées ci-dessous.
| k-epsilon inférieur à 0,8 | k-epsilon sur 0,8 | k-omega inférieur à 0,8 | k-omega sur 0,8 | |
|---|---|---|---|---|
| Ouvrage spécialisé | 6,96 % | 1,52 % | non applicable | non applicable |
| 3,7 millions de cellules | 7,66 % | 6,09 % | 9,26 % | 6,83 % |
| 7,6 millions de cellules | 7,29 % | 5,96 % | 7,83 % | 6,99 % |
| 14 millions de cellules | 7,11 % | 6,07 % | 8,22 % | 8,42 % |
| 52 millions de cellules | 5,80 % | 6,12 % | 10,79 % | 13,53 % |
[1]
Guidebook pour les prédictions CFD de l'environnement du vent urbain
[2]
Activer le numériseur


.png?mw=760&hash=d578a909f5296e100ae606d6ae168d70a1c0ca37)