Ejemplos de AIJ Caso E - Complejo de edificios en un entorno urbano real densamente construido, basado en la ciudad de Niigata

Introducción

El Instituto de Arquitectura de Japón (AIJ) ha presentado una serie de escenarios de referencia conocidos de simulación de viento.
El siguiente artículo trata sobre el "Caso E - Complejo de edificios en un área urbana real con una concentración densa de edificios de poca altura en la ciudad de Niigata".
En el siguiente texto, el escenario descrito se simula en RWIND 2 y los resultados se comparan con los resultados simulados y experimentales por AIJ.

Disposición del modelo

El caso E describe una sección de ciudad realista con un desarrollo predominantemente denso pero con edificios no muy altos. Solo unos pocos edificios se destacan significativamente por encima del resto. Una descripción más precisa de la geometría o la posición de los puntos de medición individuales es irrelevante debido a la geometría muy compleja. Los autores pusieron a disposición la geometría completa como un archivo CAD [1] y la importaron a RFEM para este artículo para poder transferirla a RWIND.

La disposición del modelo se muestra a continuación.

Construcción de modelos desde arriba - Estudio de caso de AIJ: Sección de la ciudad real con edificios bajos Ciudad de Niigata

La velocidad del flujo se evaluó en la simulación en puntos claramente definidos. También se ha publicado la posición exacta de los puntos de medición [1].

La posición de los puntos de medición se muestra a continuación.

Construcción de modelos desde arriba - Estudio de caso de AIJ: Sección de la ciudad real con edificios bajos Ciudad de Niigata

A diferencia de los modelos con menor complejidad geométrica, la configuración del nivel de detalle al crear la malla en RWIND es muy relevante en este caso. Para un nivel bajo de detalle, como el valor predeterminado 2, la malla de envoltura retráctil cierra los callejones entre edificios o patios interiores. Por lo tanto, recomendamos encarecidamente establecer el nivel de detalle en el valor máximo de 4. A continuación se muestra el problema con una densidad de malla del 15%.

Nivel 2 de detalle de malla y 15 % de densidad de malla

Nivel de detalle 4 de malla y 15 % de densidad de malla

A pesar de la misma configuración con respecto a la densidad de la malla, hay una diferencia considerable en el número de elementos y, por lo tanto, en la calidad de la malla. Por lo tanto, recomendamos usar el Nivel de detalle 4 en todos los casos y optimizar la densidad de la malla únicamente en base a esta configuración.

En el experimento AIJ, se estableció un modelo correspondiente en un túnel de viento y se midió la velocidad del viento en los puntos mencionados utilizando sondas de fibra dividida.
Los autores utilizaron tres enfoques de modelado, de los cuales solo se usa el "Código T" en este artículo. Se seleccionó este modelo porque es un solucionador comercial no especificado, en lugar de un código desarrollado individualmente que sería más fácil de aplicar para propósitos especiales, y porque RWIND también es una herramienta comercial.
La comparación de RWIND con los tres enfoques de modelado se omitió por razones de claridad. Además, los resultados de los diferentes enfoques en la publicación [1] no difieren significativamente en términos de calidad. Por lo tanto, las comparaciones presentadas aquí también son muy similares con los otros dos modelos.

Para este artículo se utilizó RWIND Pro 2.02. La estructura del modelo en RWIND se adaptó lo más cerca posible a la estructura del CFD de referencia. El estándar k–ε se utilizó como modelo de turbulencia, asumiendo un flujo estacionario. Las comparaciones hechas aquí se refieren a la dirección del viento occidental en la publicación [1]. Para las siguientes comparaciones de la velocidad relativa del viento, se estandarizó sobre 2,77 m/s.

La velocidad del flujo sobre la altura se muestra a continuación.

Los resultados experimentales del AIJ se publicaron en su sitio web [1].
Los datos mostrados de la simulación AIJ se determinaron utilizando la herramienta ENGAUGE Digitizer [2] a partir de los gráficos de la publicación [1], ya que los valores exactos para esto no se publicaron.
Sin embargo, la precisión de los puntos extraídos debería ser lo suficientemente precisa (en el intervalo de +-0,5 %) y, por lo tanto, fácilmente comparable.

Otro factor importante que influye es la configuración de "Capas de contorno", que aumenta significativamente la densidad de la malla alrededor de la condición de contorno inferior (suelo). En general, el mallado cercano al suelo influye en los resultados en esta región más de lo que sería el caso con una mayor distancia al suelo, porque la condición de contorno del suelo tiene una fuerte influencia. Debido a la geometría altamente compleja de la ciudad, se activó la configuración mencionada anteriormente y se estableció el número de capas adicionales ("NL") en 10.

Resultados y discusión

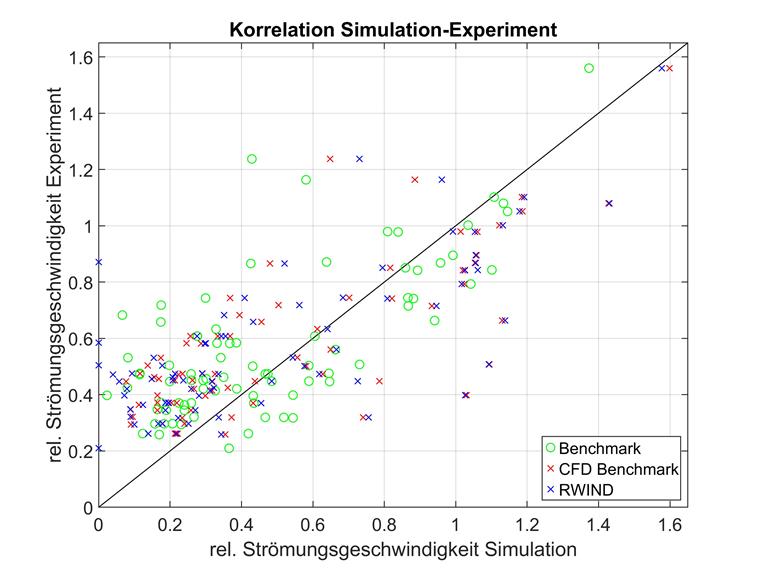
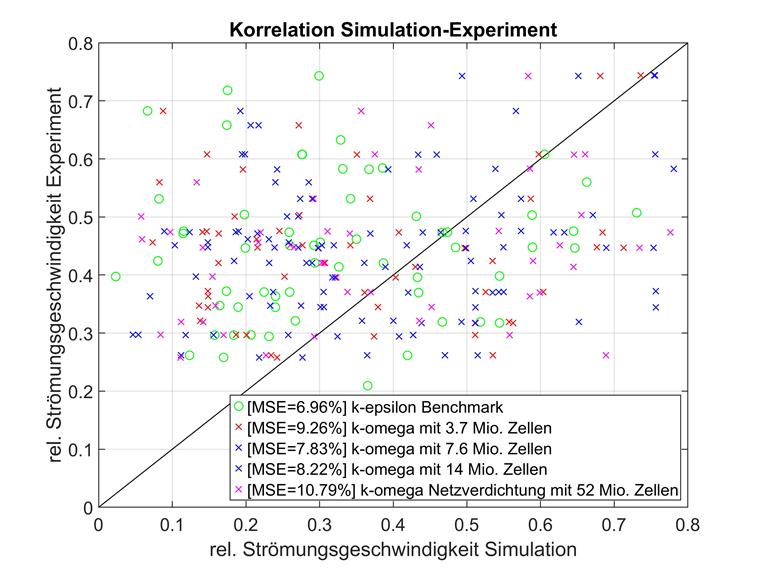
La representación de los puntos de medición posicionados tridimensionalmente mediante una numeración unidimensional simple puede ser difícil de interpretar. Por lo tanto, a continuación se muestran las comparaciones directas del experimento (eje x) y la simulación (eje y) para todos los puntos de medición. Cuanto más cerca esté un punto de medición de la línea diagonal y=x, mayor será la correlación entre la simulación y el experimento.

Correlación de las simulaciones con el experimento de recuento alto de elementos para diferentes modelos de turbulencia

La desviación cuadrática media (MSD) se utilizó como criterio de comparación, pero una comparación de los coeficientes de determinación también mostraría el mismo comportamiento, por ejemplo. Se prefirió la desviación cuadrática media al coeficiente de determinación porque la relación entre la velocidad del flujo experimental y simulada no representa una regresión y, por lo tanto, solo sería una especie de ponderación de las desviaciones individuales y no una bondad de ajuste. El MSD es geométricamente más fácil de interpretar con la misma expresividad.

La región cerca del edificio más alto se destaca en particular; es decir, aquellos puntos con la velocidad de flujo más baja en el experimento. Para este grupo de puntos, se puede observar un mayor grado de correlación entre RWIND y el experimento que entre RWIND y la simulación AIJ. Esta región se examinará más de cerca en el análisis detallado posterior.

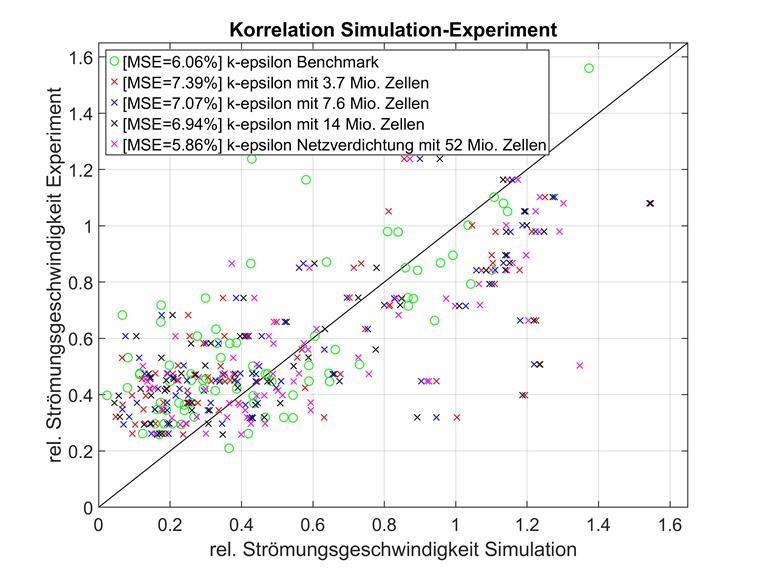
En general, es aconsejable observar más de cerca la influencia de la densidad de la malla. A continuación, se comparan las mallas de diferentes densidades con una estructura de modelo idéntica y un modelo de turbulencia RAS k-épsilon con el punto de referencia de la literatura. Los resultados se muestran a continuación.

Simulaciones que se correlacionan con el experimento Simulaciones de referencia y RWIND k-épsilon con diferentes números de elementos

Los puntos de datos individuales se encuentran en el rango de la velocidad relativa del flujo, especialmente entre 0 y 0,8. La correlación con los experimentos a veces difiere significativamente dentro y fuera del intervalo indicado. Para una mejor comparabilidad, solo los puntos de datos con rel. las velocidades de flujo por debajo de 0,8 se muestran para ambos ejes y las desviaciones cuadráticas medias se recalculan en consecuencia.

Correlación de las simulaciones con el experimento en rel. Velocidades de flujo por debajo de 0,8 Simulaciones de referencia y RWIND k-épsilon con diferentes números de elementos

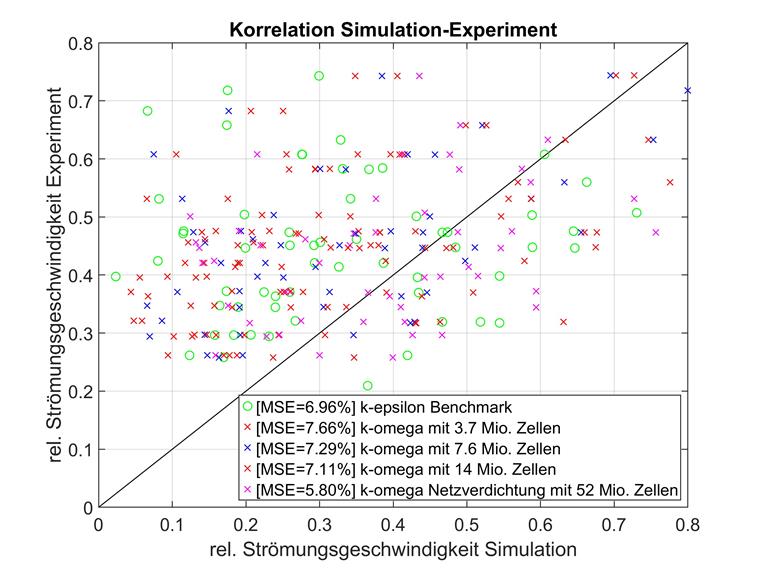
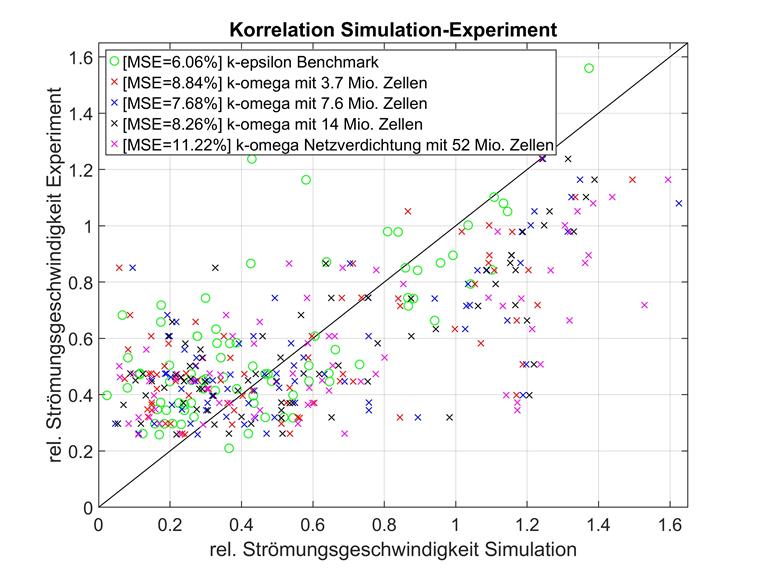
También se realizó un estudio de convergencia de malla para el modelo de turbulencia k-omega y las mismas formaciones de malla. Los resultados se muestran a continuación.

Simulaciones que se correlacionan con el experimento Simulaciones de referencia y RWIND k-omega con diferentes números de elementos

Al igual que con la comparación de los modelos k-épsilon, las velocidades de flujo bajas se compararon por separado para k-omega. Estos datos se visualizan a continuación.

Correlación de las simulaciones con el experimento en rel. Velocidades de flujo por debajo de 0,8 Simulaciones de referencia y RWIND k-omega con diferentes números de elementos

Aquí se confirman los resultados de la comparación de los modelos k-épsilon. Para mallas de resolución más baja, las velocidades de flujo relativas por debajo de 0,8 se desvían más del punto de referencia experimental que de los puntos de datos medios generales.
Sin embargo, con un número creciente de elementos, este efecto se invierte, de modo que los modelos de malla estrecha se desvían aún menos para las velocidades de flujo relativas bajas.

Los puntos incluidos en esta consideración por separado tienden a estar ubicados en áreas más densamente urbanizadas. La ubicación de los puntos podría explicar los mejores resultados de las mallas más complejas, porque las mallas más finas pueden representar la geometría con mayor precisión. Dado que la geometría real influye más en estos puntos que en los puntos con velocidades de flujo relativas superiores a 0,8, la malla más densa se ajusta mejor al experimento.

Residuos para dos modelos de turbulencia - Caso E

Estas observaciones coinciden con las expectativas de varios modelos de turbulencia. Para el uso de k-omega, recomendamos aumentar considerablemente el número de iteraciones máximas. El valor predeterminado de 300 se debe aumentar manualmente hasta al menos 1.000.

En conclusión, la comparación de ambos modelos de turbulencia en RWIND es menos clara para el caso E que para el caso D, por ejemplo. En este ejemplo de referencia, el modelo k-épsilon es superior para cualquier densidad de malla. Además, k-épsilon se escala mucho mejor que k-omega a medida que aumenta el número de elementos. Los resultados del último modelo de turbulencia no parecen seguir ninguna convergencia con una mayor densidad de malla. El modelo de complejidad media da los mejores resultados, mientras que el modelo muy complejo muestra la mayor desviación con diferencia del punto de referencia experimental. Por lo tanto, los resultados de k-épsilon están dentro del rango esperado y también pueden superar la simulación de referencia si la densidad de la malla es alta, pero no se pueden sacar conclusiones congruentes para k-omega. La desviación muy alta para el modelo k-omega más grande en particular es un misterio. Presumiblemente, no se pudo identificar de manera concluyente un factor de influencia de k-omega, pero que no afecte igualmente a k-épsilon.

Para una comparación más clara de la simulación de referencia con los resultados de RWIND, se recomienda ver las velocidades de flujo como una imagen en color de la botella.
La sección considerada alrededor del edificio más alto se adaptó a la de los autores [1]. El resultado se muestra a continuación.

Velocidad del flujo alrededor del edificio más alto - Caso E de AIJ

Por razones de derechos de autor, las imágenes en falso color no se comparan una al lado de la otra en este punto.

Además, la imagen en falso color de la velocidad del flujo sobre toda la ciudad se mostró al nivel de los puntos de medición.

Velocidad del flujo en toda la ciudad - Caso E de AIJ

También hay una muy buena correlación con la simulación de la literatura. Las desviaciones más pequeñas ocurren principalmente en las esquinas del edificio con un flujo brusco, pero estas son pequeñas en términos de cantidad y espacialmente muy limitadas.

Conclusión

Las desviaciones cuadráticas medias de diferentes combinaciones de número de elemento y modelo de turbulencia se resumen a continuación.

A continuación, hay una comparación de los diferentes rangos de velocidad.

[1] Guía para las predicciones de la dinámica de fluidos computacional (CFD) del entorno eólico urbano
[2] Digitalizador Engauge

482x

61x

Ejemplo de caso E de AIJ: complejo de edificios en un entorno urbano real densamente construido, similar a la ciudad de Niigata