Przykłady AIJ Case E - Kompleks budynków w rzeczywistym obszarze miejskim o gęstej koncentracji budynków w mieście Niigata

Wstęp

Japoński Instytut Architektury (AIJ) przedstawił kilka dobrze znanych scenariuszy odniesienia dla symulacji wiatru.
Poniższy artykuł dotyczy "Przypadku E - Zespół budynków na rzeczywistym obszarze miejskim ze zwartą koncentracją niskiej zabudowy w mieście Niigata".
W poniższym tekście opisany scenariusz jest symulowany w RWIND 2, a wyniki są porównywane z wynikami symulacji i eksperymentów przez AIJ.

Układ modelu

Przypadek E opisuje realistyczny fragment miasta z przeważającą gęstą zabudową, ale nie bardzo wysoką zabudową. Tylko nieliczne budynki stoją znacznie ponad innymi. Ze względu na bardzo złożoną geometrię, dokładniejszy opis geometrii lub położenia poszczególnych punktów pomiarowych nie jest istotny. Kompletna geometria została udostępniona przez autorów jako plik CAD [1] i zaimportowana do programu RFEM na potrzeby tego artykułu w celu przeniesienia do RWIND.

Układ modelu pokazano poniżej.

Modelowanie budynku z góry - studium przypadku AIJ: prawdziwy fragment miasta z niską zabudową Niigata City

W symulacji oceniano prędkość przepływu w wyraźnie określonych punktach. Dokładne położenie punktów pomiarowych również zostało opublikowane [1].

Położenie punktów pomiarowych pokazano poniżej.

Modelowanie budynku z góry - studium przypadku AIJ: prawdziwy fragment miasta z niską zabudową Niigata City

W przeciwieństwie do modeli o mniejszym stopniu złożoności geometrycznej, ustawienie poziomu szczegółowości podczas tworzenia siatki w RWIND jest w tym przypadku bardzo istotne. W przypadku niskiego poziomu szczegółowości, takiego jak domyślna wartość 2, siatka opakowaniowa zamyka alejki między budynkami lub wewnętrzne dziedzińce. Dlatego zdecydowanie zaleca się ustawienie poziomu szczegółowości na maksymalną wartość 4. Poniżej przedstawiono problem z gęstością siatki wynoszącej 15%.

Poziom szczegółowości siatki 2 i 15% gęstości siatki

Poziom uszczegółowienia siatki 4 i 15% gęstość sieci

Pomimo tego samego ustawienia w odniesieniu do gęstości siatki, występuje znaczna różnica w liczbie elementów, a tym samym w jakości siatki. Dlatego we wszystkich przypadkach zaleca się stosowanie Poziomu szczegółu 4 i optymalizację gęstości siatki wyłącznie na podstawie tego ustawienia.

W eksperymencie z AIJ, odpowiedni model ustawiono w tunelu aerodynamicznym, a prędkość wiatru mierzono we wspomnianych punktach za pomocą sond z włókna szklanego.
Autorzy zastosowali trzy podejścia do modelowania, z których w tym artykule wykorzystano tylko "kod T". Model ten został wybrany, ponieważ jest to nieokreślony komercyjny solwer, a nie indywidualnie opracowana norma, którą łatwiej byłoby zastosować do specjalnych celów, a także dlatego, że RWIND jest również narzędziem komercyjnym.
Dla zachowania przejrzystości pominięto porównanie RWIND ze wszystkimi trzema metodami modelowania. Ponadto wyniki uzyskane przy użyciu różnych podejść w publikacji [1] nie różnią się znacząco pod względem jakości. Przedstawione tutaj porównania są zatem bardzo podobne do dwóch pozostałych modeli.

W artykule wykorzystano program RWIND Pro 2.02. Struktura modelu w RWIND została dostosowana w możliwie największym stopniu do struktury CFD odniesienia. Jako model turbulencji zastosowano standardową k–ε przy założeniu, że przepływ jest stały. Porównania dokonane w publikacji [1] odnoszą się do zachodniego kierunku wiatru. Dla poniższych porównań względna prędkość wiatru została znormalizowana z prędkością powyżej 2,77 m/s.

Prędkość przepływu na wysokości pokazano poniżej.

Wyniki eksperymentalne AIJ zostały opublikowane na ich stronie internetowej [1].
Wyświetlane dane symulacji AIJ zostały określone za pomocą programu ENGAUGE Digitizer [2] na podstawie wykresów opublikowanych w publikacji [1], ponieważ dokładne wartości nie zostały opublikowane.
Dokładność wyodrębnionych punktów powinna być jednak wystarczająco dokładna (w zakresie +-0,5%), a zatem łatwo porównywalna.

Innym ważnym czynnikiem jest ustawienie „Warstwy graniczne”, które znacznie zwiększa gęstość siatki wokół dolnej granicy warunku (grunt). Ogólnie rzecz biorąc, siatkowanie w pobliżu gruntu wpływa na wyniki w tym obszarze w większym stopniu niż w przypadku większej odległości od gruntu, ponieważ warunek brzegowy gruntu ma duży wpływ. Ze względu na bardzo złożoną geometrię miasta aktywowano wspomniane ustawienie, a liczba dodatkowych warstw („NL”) została ustawiona na 10.

Wyniki i dyskusja

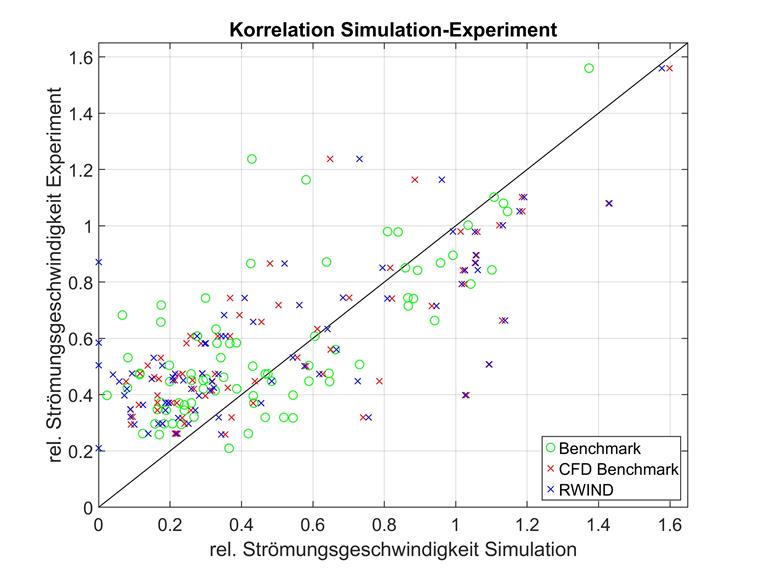
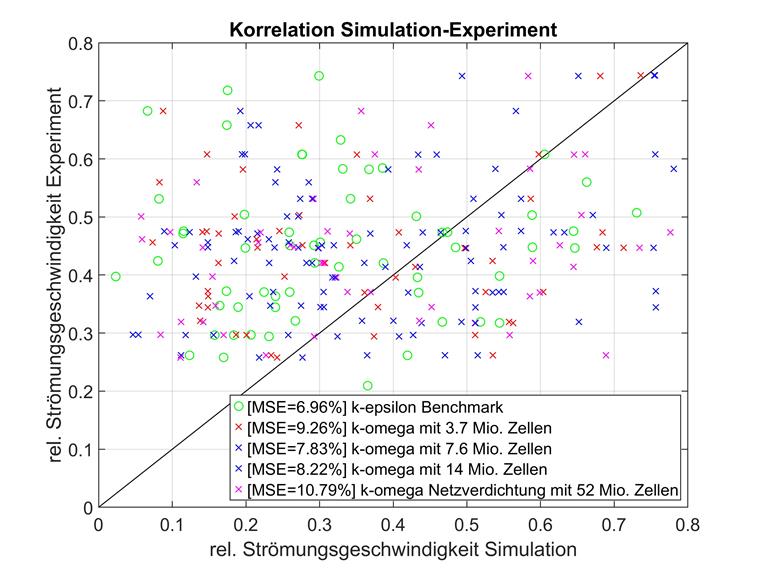
Punkty pomiarowe umieszczone w przestrzeni trójwymiarowej przedstawione za pomocą prostej jednowymiarowej numeracji mogą być trudne do zinterpretowania. Dlatego poniżej pokazano bezpośrednie porównanie eksperymentu (oś x) i symulacji (oś y) dla wszystkich punktów pomiarowych. Im bliżej linii ukośnej y=x znajduje się punkt pomiarowy, tym większa jest korelacja między symulacją a eksperymentem.

Korelacja symulacji z eksperymentem z dużą liczbą pierwiastków dla różnych modeli turbulencji

Jako kryterium porównawcze zastosowano odchylenie średniokwadratowe (MSD), ale na przykład porównanie współczynników determinacji wykazałoby takie samo zachowanie. Preferowano średnią odchyłkę kwadratową od współczynnika determinacji, ponieważ stosunek prędkości eksperymentalnej i symulowanej nie stanowi regresji, a zatem byłby tylko rodzajem ważenia poszczególnych odchyleń, a nie wartością dopasowania. MSD jest geometrycznie łatwiejszy do interpretacji z taką samą wyrazistością.

Szczególnie wyróżnia się obszar w pobliżu najwyższego budynku; czyli punkty o najmniejszej prędkości przepływu w eksperymencie. Dla tej grupy punktów można zaobserwować wyższy stopień korelacji między RWIND a eksperymentem niż między RWIND a symulacją AIJ. Obszar ten zostanie zbadany dokładniej w późniejszej szczegółowej analizie.

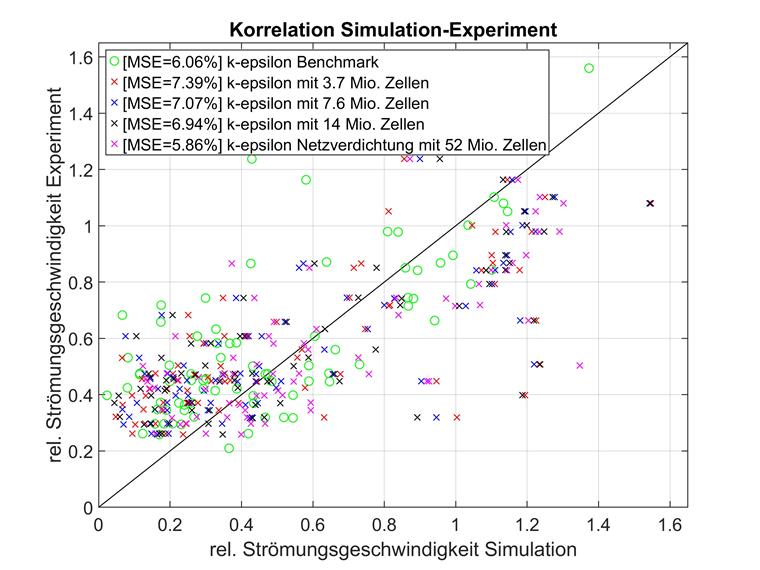
Zasadniczo zaleca się bliższe przyjrzenie się wpływowi gęstości siatki. Poniżej porównano siatki o różnych gęstościach z identyczną konstrukcją modelu oraz modelem turbulencji k-epsilon RAS z modelem literaturowym. Wyniki pokazano poniżej.

Symulacje skorelowane z eksperymentem Symulacje typu Benchmark i RWIND k-epsilon z różnymi numerami pierwiastków

Poszczególne punkty danych leżą w zakresie względnej prędkości przepływu, zwłaszcza między 0 a 0,8. Korelacja z eksperymentami czasami różni się znacznie w podanym zakresie i poza nim. Dla lepszej porównywalności danych należy użyć tylko punktów o rel. prędkości przepływu poniżej 0,8 dla obu osi i odpowiednio ponownie obliczone odchylenia średniokwadratowe.

Korelacja symulacji z doświadczeniem w rel. Prędkości przepływu poniżej 0,8 Symulacje typu Benchmark i RWIND k-epsilon z różnymi numerami pierwiastków

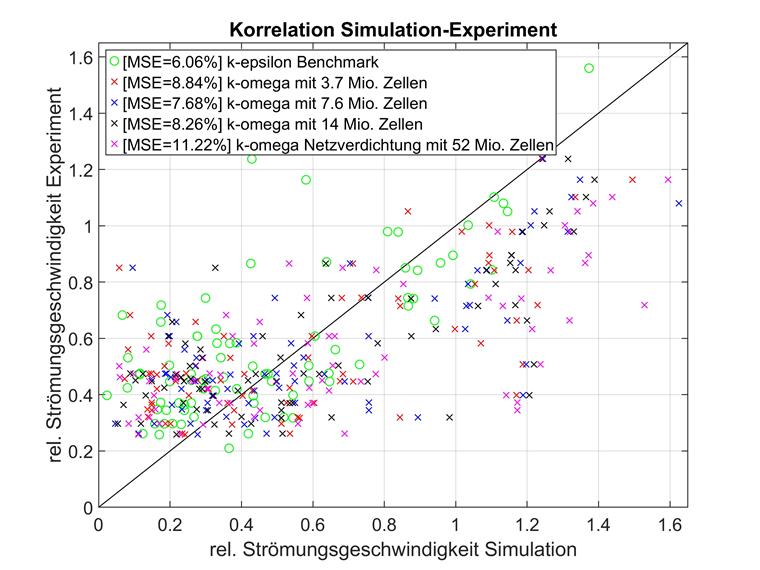
Przeprowadzono również badanie zbieżności siatki dla modelu turbulencji k-omega i tych samych formacji siatki. Wyniki pokazano poniżej.

Symulacje skorelowane z eksperymentem Symulacje k-omega Benchmark i RWIND z różną liczbą pierwiastków

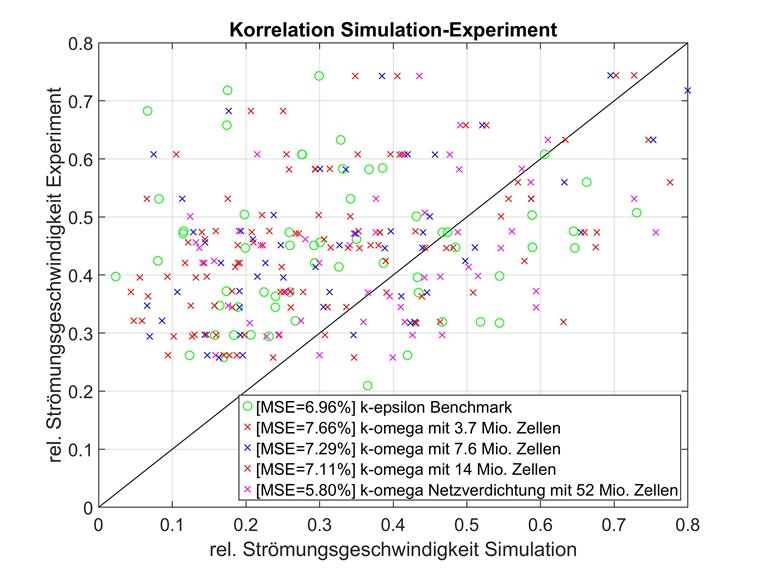
Podobnie jak w przypadku porównywania modeli k-epsilon, niskie prędkości przepływu zostały porównane osobno dla k-omega. Dane te zostały zwizualizowane poniżej.

Korelacja symulacji z doświadczeniem w rel. Prędkości przepływu poniżej 0,8 Symulacje k-omega Benchmark i RWIND z różną liczbą pierwiastków

Potwierdzają to wyniki porównania modeli k-epsilon. W przypadku siatek o niższej rozdzielczości względne prędkości przepływu poniżej 0,8 bardziej odbiegają od eksperymentalnego poziomu odniesienia niż od średnich ogólnych punktów danych.
Jednak wraz ze wzrostem liczby elementów efekt ten ulega odwróceniu, dzięki czemu modele o gęstej siatce wykazują jeszcze mniejsze odchylenia w przypadku małych prędkości przepływu względnego.

Punkty uwzględnione w tym osobnym rozpatrzeniu są zazwyczaj zlokalizowane w obszarach bardziej gęsto zabudowanych. Położenie punktów może wyjaśniać lepsze wyniki bardziej złożonych siatek, ponieważ drobniejsze siatki mogą dokładniej odwzorować geometrię. Ponieważ rzeczywista geometria wpływa na te punkty bardziej niż punkty o względnych prędkościach przepływu powyżej 0,8, siatka o większej gęstości lepiej pasuje do eksperymentu.

Wartości szczątkowe dla dwóch modeli turbulencji - przypadek E

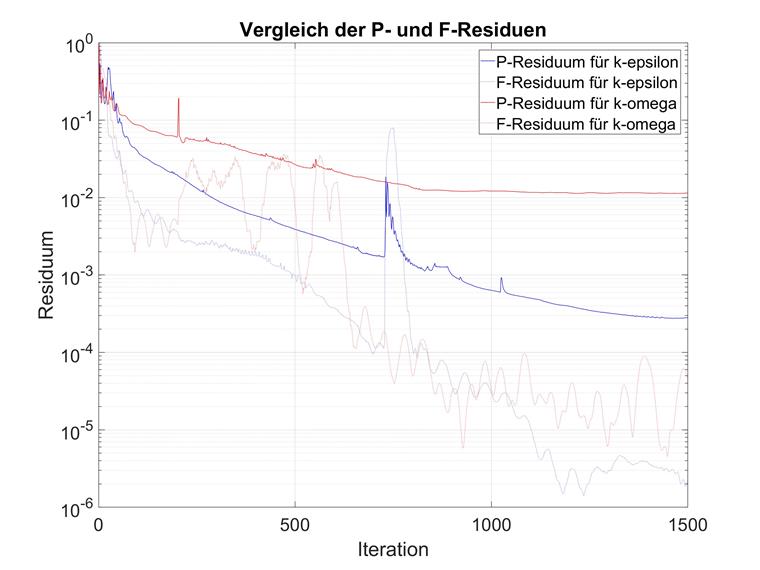
Obserwacje te są zbieżne z oczekiwaniami dotyczącymi różnych modeli turbulencji. Aby zastosować k-omega, zalecamy znaczne zwiększenie liczby maksymalnych iteracji. Domyślną wartość 300 należy ręcznie zwiększyć do co najmniej 1000.

Podsumowując, porównanie obu modeli turbulencji w RWIND jest mniej jasne w przypadku przypadku E niż na przykład w przypadku D. W tym przykładzie referencyjnym model k-epsilon jest lepszy dla dowolnej gęstości siatki. Co więcej, k-epsilon skaluje się znacznie lepiej niż k-omega wraz ze wzrostem liczby pierwiastków. Wyniki drugiego modelu turbulencji nie wykazują zbieżności przy większej gęstości siatki. Model o średniej złożoności daje najlepsze wyniki, podczas gdy model bardzo złożony wykazuje największe odchylenie od eksperymentalnego punktu odniesienia. W ten sposób wyniki k-epsilon mieszczą się w oczekiwanym zakresie i mogą również być lepsze od symulacji referencyjnej, jeśli gęstość siatki jest wysoka, ale nie można wyciągnąć zgodnych wniosków dla k-omega. Zagadką jest bardzo duże odchylenie, szczególnie w przypadku największego modelu k-omega. Przypuszczalnie nie udało się zidentyfikować współczynnika wpływającego na k-omega, ale nie mającego takiego samego wpływu na k-epsilon.

Aby lepiej porównać symulację referencyjną z wynikami RWIND, zaleca się wyświetlić prędkości przepływu jako kolorowy obraz butelki.
Analizowany przekrój wokół najwyższego budynku został dostosowany do przekroju autorów [1]. Wynik pokazano poniżej.

Prędkość przepływu wokół najwyższego budynku - AIJ Case E

Ze względu na prawa autorskie obrazy w kolorze sztucznym nie są na tym etapie porównywane.

Ponadto, na poziomie punktów pomiarowych pokazano fałszywy kolorowy obraz prędkości przepływu na terenie całego miasta.

Prędkość przepływu w całym mieście - AIJ Case E

Istnieje również bardzo dobra korelacja z symulacją literaturową. Mniejsze odchylenia występują głównie w narożach budynku o ostrym przepływie, są one jednak niewielkie ilościowo i bardzo ograniczone przestrzennie.

Uwagi końcowe

Poniżej zestawiono średnie odchylenia kwadratowe dla różnych kombinacji numeru elementu i modelu turbulencji.

Poniżej znajduje się porównanie różnych zakresów prędkości.

[1] Poradnik dla prognoz CFD dla wiatru w miastach
[2] Zaangażuj digitizera

484x

61x

Przykład AIJ przypadek E - Zespół budynków w rzeczywistym gęsto zabudowanym środowisku miejskim, na wzór miasta Niigata