|
作者
|
David Bonilla
|
|
学校
|
Bauhaus University Weimar, Germany |
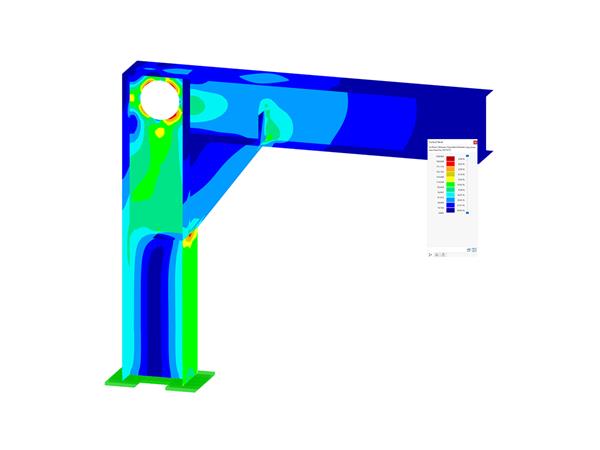
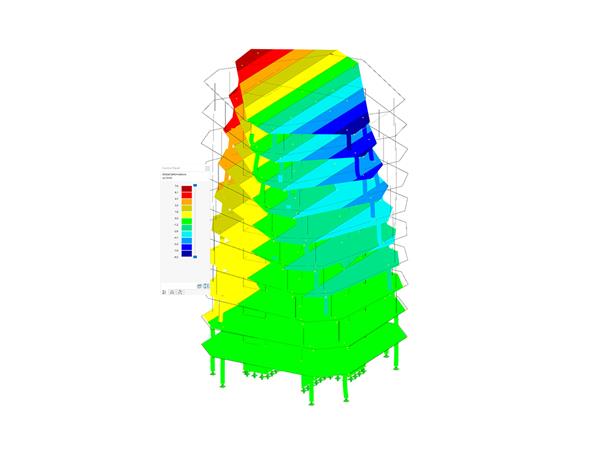
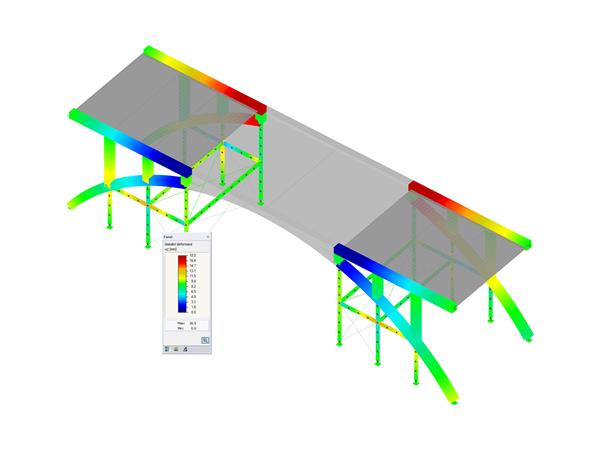
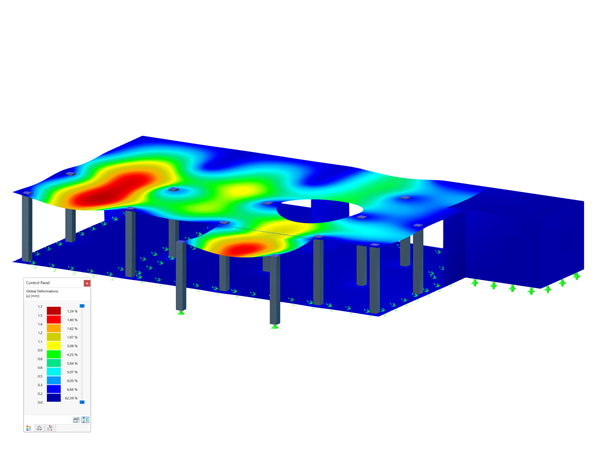
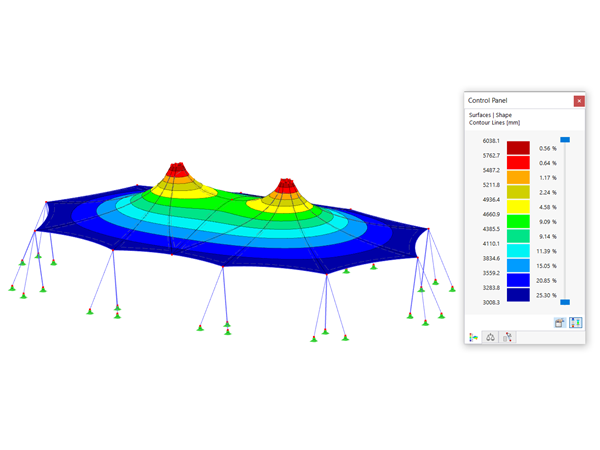
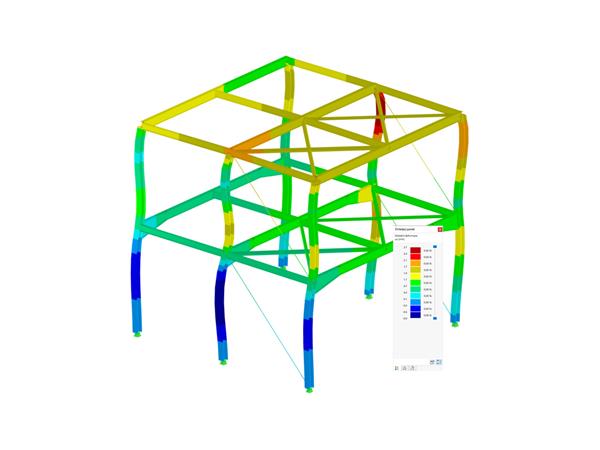
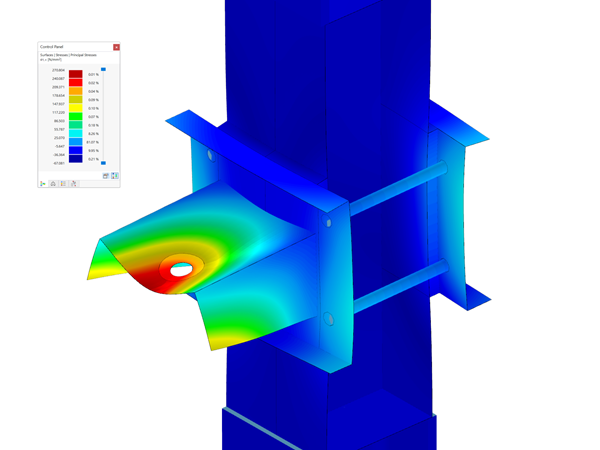
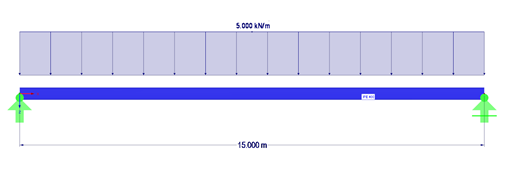
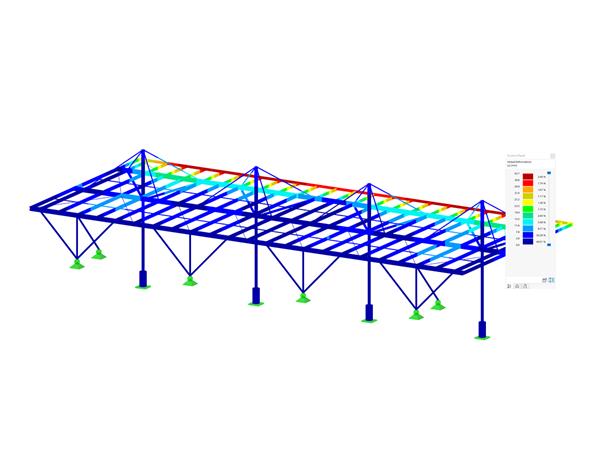
已经使用商业软件 RFEM 按照 SOT 和 GNA 方法对该问题进行了数值分析。 进行模拟时考虑了以下变量: 4 个结构体系,2 种有限元网格,43 个截面(38 个开口,5 个闭合)和 3 种外部荷载。 每个分析都进行 10 次,在每一次中都将外部荷载增加到最大值的 100 %。 验算了临界荷载、位移、内力和应力。
结果表明,随着位移的增加,SOT 和 GNA 之间的差异越来越大。 对于荷载也有相同的行为,力越大,位移就越大,因此两种方法之间的差异也越大。
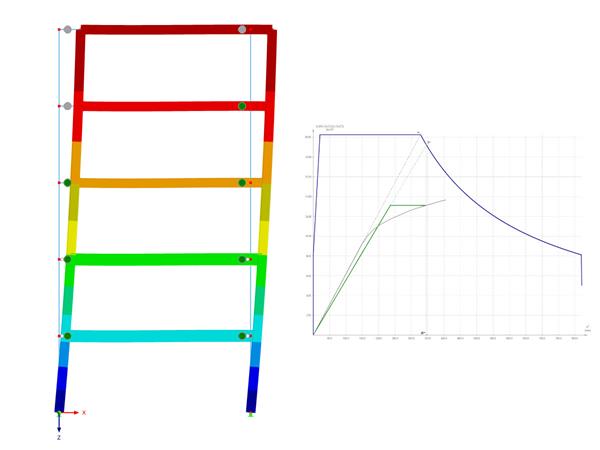
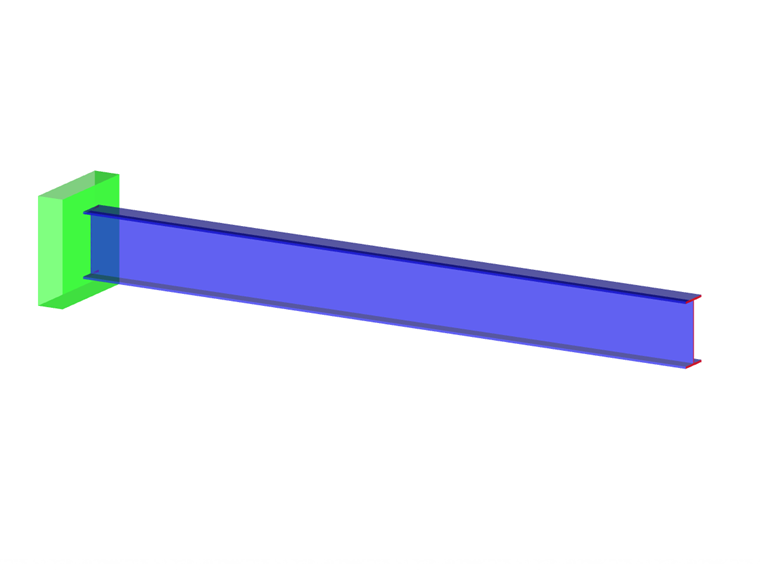
对于封闭截面,位移和内力的变化很小。 使用一维杆件单元可以简化其分析。 如果旋转是封闭的,那么旋转将被限制在截面的承载力之内。 此外,封闭型材具有出色的抗扭性能,对于这种情况可以使用 GNA 的近似 SOT 方法进行计算。
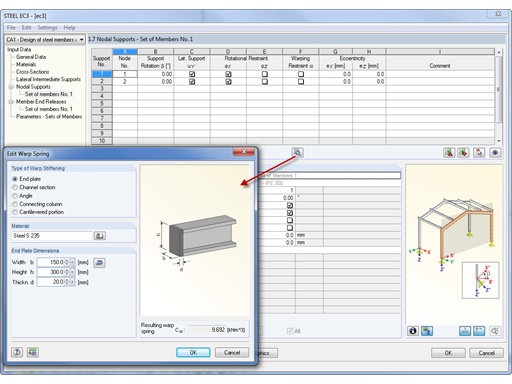
最后,根据研究的结果得出了一个阶段,在该阶段 SOT 方法以拟合曲线的形式给出了足够可靠的结果,该阶段对于 IPE 和 HEB 曲线也同样适用。 对于受弯和受扭钢杆件应该进行何种分析类型的拟合,软件提供了一种实用的拟合曲线。 选择 SOT 还是 GNA,主要取决于截面形状和荷载大小。 此外,边界条件和荷载类型也非常重要。 最后一点表明,对于不同的荷载分布,曲线仍然可以提供一个很好的估算结果。 IPE 拟合曲线也可用于 UPE 拟合。









.png?mw=350&hash=154cfb9bf427390b9a61c822d106bf243d0c64e8)







,_LC1_LI.jpg?mw=350&hash=63fa8f314e69d0e0cb39a37725259712c559d025)
,_LC1__LI.jpg?mw=350&hash=197fe455305453516450354c49b05b6f43e4a2cf)
,_LC1__LI.jpg?mw=350&hash=b3482f816b157606c7c88c75bfa2b52c5a8deab0)
,_LC1__LI.jpg?mw=350&hash=80caf81f6c0a20df0f1d44557864ff0117ccdd28)




.png?mw=512&hash=4a84cbc5b1eacf1afb4217e8e43c5cb50ed8d827)















_1.jpg?mw=350&hash=ab2086621f4e50c8c8fb8f3c211a22bc246e0552)




-querkraft-hertha-hurnaus.jpg?mw=350&hash=3306957537863c7a7dc17160e2ced5806b35a7fb)

.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)