Der Zustand des eingeschlossenen Gases kann mit Hilfe dieser Annahmen über ein thermodynamisches Gleichgewicht beschrieben werden. Daraus ergibt sich folgende allgemeine Gasgleichung:
p ∙ V = n ∙ R ∙ T
mit den Zustandsgrößen
p = Druck
V = Volumen
n = Stoffmenge
R = universelle Gaskonstante
T = Temperatur
Eigenschaften idealer Gase
Wenn man bestimmte Zustandsgrößen in der allgemeinen Gasgleichung konstant hält, ergeben sich spezielle Eigenschaften des idealen Gases. Die Kenntnis dieser Eigenschaften ist für die Verwendung von idealen Gasen in der Tragwerksanalyse hilfreich und hilft gewisse Lastzustände entsprechend zu simulieren.
Isotherme Zustandsänderung (Boyle-Mariotte)
Hält man die Größen T und n konstant und erhöht den einwirkenden Druck p, wird das Volumen V der betrachteten Gaseinheit verkleinert.
以下规定适用:
Isobare Zustandsänderung (Gay-Lussac)
Hält man die Größen p und n konstant und erhöht die einwirkende Temperatur T, wird das Volumen V der betrachteten Gaseinheit größer.
以下规定适用:
Isochore Zustandsänderung (Amotons)
Hält man die Größe V und n konstant und erhöht die einwirkende Temperatur T, erhöht sich der Druck p der betrachteten Gaseinheit.
以下规定适用:
Anwendung in der Baustatik
In der Baustatik werden eingeschlossene Gase meist zur Übertragung von externen Kräften verwendet. Die Anforderung ist hier, dass eine lokal wirkende Kraft an einer bestimmten Stelle auf der Volumenhülle über das eingeschlossene Gas an alle anderen Seiten der Volumenhülle transportiert werden kann.
Diese Eigenschaft wird zum Beispiel bei Isolierglasscheiben oder aufgeblasenen Membrankissen verwendet. In beiden Fällen ist die Volumenhülle aus tragfähigen Elementen beschrieben und mit einem Gas gefüllt. Bei Isolierglasscheiben besteht die Volumenbegrenzung aus biegesteifen Schalenelementen und bei Membrankissen aus biegeschlaffen Membranelementen. Bei beiden Fällen greift jedoch beispielsweise die Wind- oder Schneelast an einer Seite der Volumenbegrenzung an und wird über das eingeschlossene Gas an die benachbarten Volumenbegrenzungen übertragen.
Da sich bei den im Bauwesen betrachteten Lastsituationen die Temperatur nicht plötzlich ändert, wird meist in der Volumenhülle ein ideales Gas mit isothermen Zustandseigenschaften simuliert.
Umsetzung in RFEM
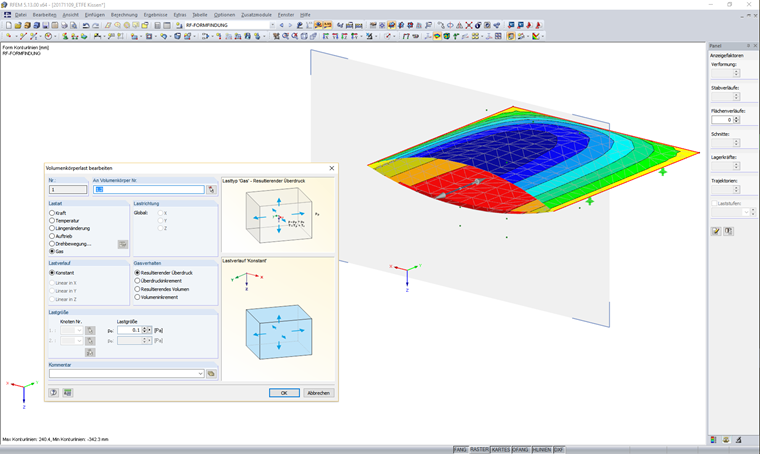
In RFEM gibt es Volumendefinitionen. Diese Volumina werden über die umliegenden Oberflächen beschrieben. In solch einer Volumenzelle aus umliegenden Schalen- und Volumenbauteilen kann eine Volumendefinition mit dem Typ Gas einbeschrieben werden. Dieses resultierende Gasvolumen benötigen eine Beschreibung des eingeschlossenen Gases und eine Festlegung der atmosphärischen Zustandsgrößen. Die atmosphärischen Zustandsgrößen haben keine Wirkung auf das eingeschlossene Volumen und beschreiben nur eine Anfangssituation für die Simulation.
In den zugeordneten Lastfällen kann dann für jedes Gasvolumen eine entsprechende Volumenlast aufgebracht werden. Zur Simulation von offenen oder geschlossene Volumina gibt es die Möglichkeit, resultierende Drücke/Volumen beziehungsweise Druck-/Volumenänderungen vorzugeben.