Stav uzavřeného plynu lze popsat za těchto předpokladů stavem termodynamické rovnováhy. Lze tak formulovat následující obecnou stavovou rovnici plynu:
p ∙ V = n ∙ R ∙ T
se stavovými proměnnými
p = tlak
V = objem
n = látkové množství
R = molární plynová konstanta
T = teplota
Vlastnosti ideálních plynů
Pokud jsou určité stavové veličiny v obecné rovnici plynu konstantní, lze pozorovat zvláštní vlastnosti ideálního plynu. Pro použití ideálních plynů ve statických výpočtech je užitečné tyto vlastnosti znát, mohou nám pomoci vhodně simulovat určité zatěžovací stavy.
Izotermická změna stavu (Boyleův-Mariottův zákon)
Pokud jsou veličiny T a n konstantní a zvyšuje se působící tlak p, zmenšuje se objem V sledované jednotky plynu.
Přitom platí:
Izobarická změna stavu (Gay-Lussacův zákon)
Pokud udržujeme veličiny p a n konstantní a zvyšujeme teplotu T, zvětšuje se objem V sledované jednotky plynu.
Přitom platí:
Izochorická změna stavu (Amontons)
Jestliže udržujeme veličiny V a n konstantní a zvyšujeme působící teplotu T, zvyšuje se tlak p sledované jednotky plynu.
Přitom platí:
Použití ve statice
Ve statice se uzavřené plyny obvykle používají pro přenos vnějších sil. Požadavkem přitom je, aby síla působící lokálně na určitém místě pláště daného tělesa mohla být přenesena uzavřeným plynem na všechny ostatní strany pláště tělesa.
Tato vlastnost se využívá například u izolačních skel nebo u vzduchových membránových polštářů. V obou případech je plášť tělesa složen z prvků schopných přenášet zatížení a naplněn plynem. U izolačních skel je těleso vymezeno ohybově tuhými skořepinovými prvky, zatímco v případě membránových polštářů těleso vymezují membránové prvky s prakticky nulovou ohybovou tuhostí. V obou případech ovšem působí například zatížení větrem nebo sněhem na jednu stranu pláště tělesa a uzavřený plyn ho přenáší na okolní hraniční prvky tělesa.
Vzhledem k tomu, že se v uvažovaných zatěžovacích situacích ve stavebnictví teplota nemění náhle, většinou se v tělese modeluje ideální plyn s izotermickými stavovými vlastnostmi.
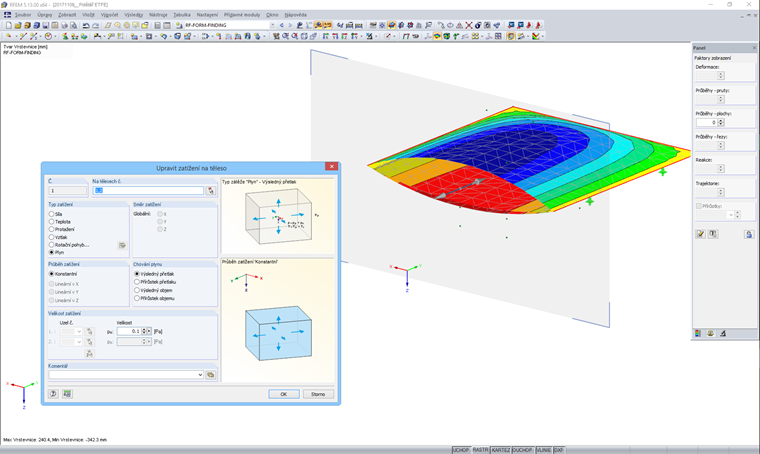
Postup v programu RFEM
V programu RFEM lze zadávat tělesa, která jsou vymezena hraničními plochami. V takové objemové buňce, kterou obklopují skořepinové či membránové prvky, lze definovat těleso typu Plyn. U tohoto tělesa je potřeba definovat uzavřený plyn a stanovit atmosférické stavové veličiny. Tyto atmosférické stavové veličiny nemají žádný vliv na uzavřené těleso a popisují pouze počáteční situaci pro simulaci.
V přiřazených zatěžovacích stavech lze na každé těleso typu Plyn vnést odpovídající zatížení. Pro simulaci otevřených nebo uzavřených těles můžeme předem zadat výsledné tlaky/objemy, případně změny tlaku/objemu.