Voltar para a base de dados de conhecimento

6246x

000585

2021-02-15

Cálculo de molas de empenamento para consideração na análise de encurvadura por flexão-torção para secções abertas

Bei offenen Querschnitten erfolgt der Abtrag von Torsionsbelastung vor allem über sekundäre Torsion, da die St. Venantsche Torsionssteifigkeit gegenüber der Wölbsteifigkeit gering ist. Besonders für den Biegedrillknicknachweis sind daher Wölbversteifungen im Querschnitt interessant, da diese die Verdrehung erheblich reduzieren können. Hierfür bieten sich beispielsweise Stirnplatten oder eingeschweißte Steifen und Profile an.

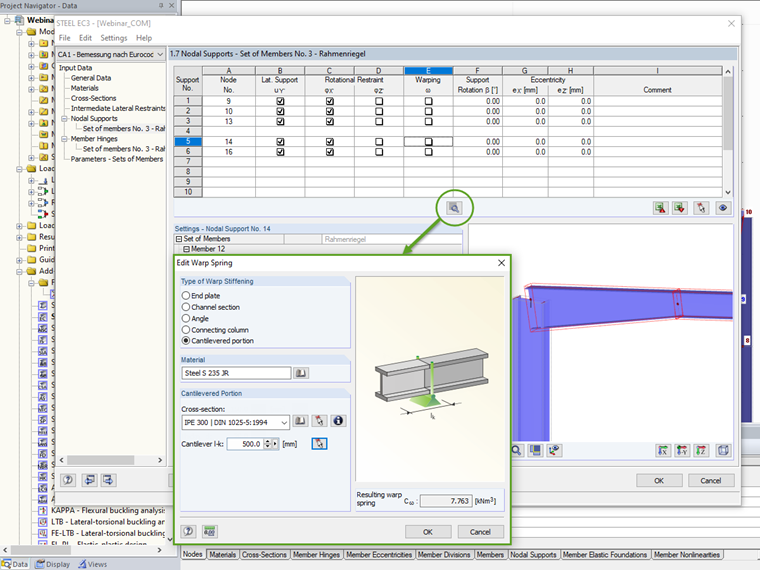
Cálculo da mola empenada

Se for aplicada uma tensão de empenamento, esta corresponde à restrição completa do empenamento da secção, por exemplo através de uma placa de extremidade rígida. Na realidade, no entanto, esta restrição total geralmente não é dada porque as placas de extremidade não são infinitamente rígidas, mas também deformáveis. Ao introduzir os apoios nodais, os módulos de dimensionamento para estruturas em aço e alumínio permitem um cálculo direto das molas de empenamento a partir das variantes apresentadas abaixo de acordo com [1].

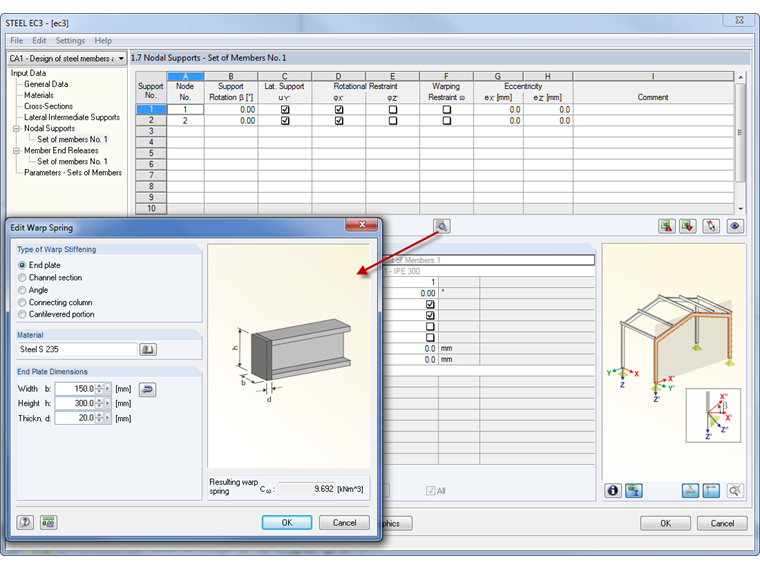
Chapa de extremidade

Restrição de empenamento através da placa de extremidade

A restrição ao empenamento da placa de extremidade resulta da rigidez à torção da placa ligada.

C_{ω} = \frac{1}{3} \cdot G \cdot b \cdot h \cdot t ³

C_ω	Wölbfeder
G	Schubmodul
b	Breite der Stirnplatte
h	Höhe der Stirnplatte
t	Dicke der Stirnplatte

Mola de empenamento para restrição de empenamento através da placa de extremidade

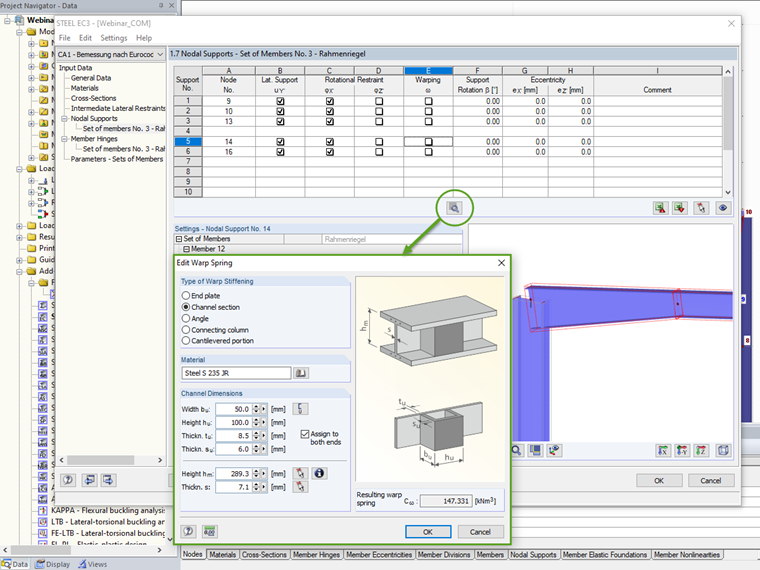
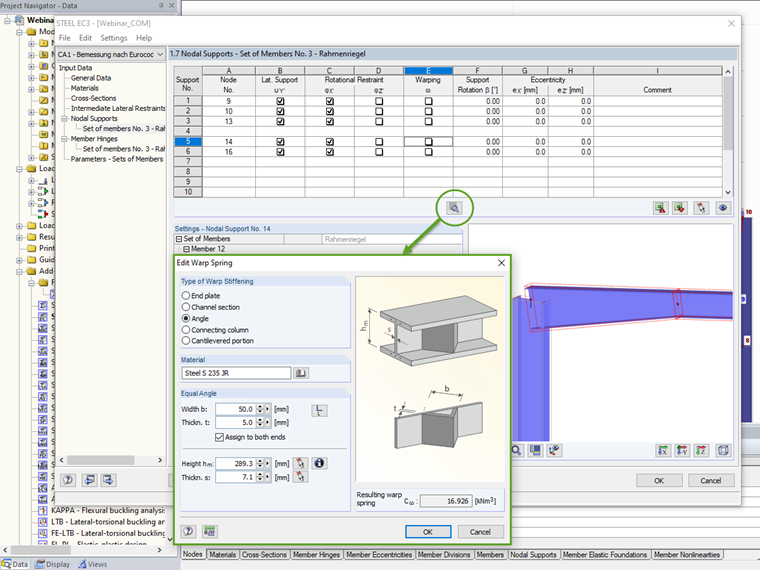
Canais e secções em ângulo

Restrição de empenamento através da secção de canal soldada

Restrição de empenamento através de secção angular soldada

A restrição ao empenamento por anteparas transversais de rigidez à torção é significativamente maior do que pelas chapas de extremidade e o balanço da viga, devido à maior rigidez à torção. Os reforços em U ou em L soldados num lado juntamente com a alma formam uma viga em forma de caixão; se disposta em ambos os lados, resulta uma viga em caixa com dimensões maiores.

C_{ω} = G \cdot h_{m} \cdot \frac{4 \cdot A_{m}^{2}}{\sum \frac{l_{i}}{t_{i}}}

C_ω	Wölbfeder
G	Schubmodul
h_m	Abstand der Mittelebenen der Flansche des Trägers
A_m	Von der Mittellinie eingeschlossene Fläche
l_i	Seitenlänge
t_i	Blechdicke

Mola de empenamento para restrição de empenamento através de canal soldado ou secção angular

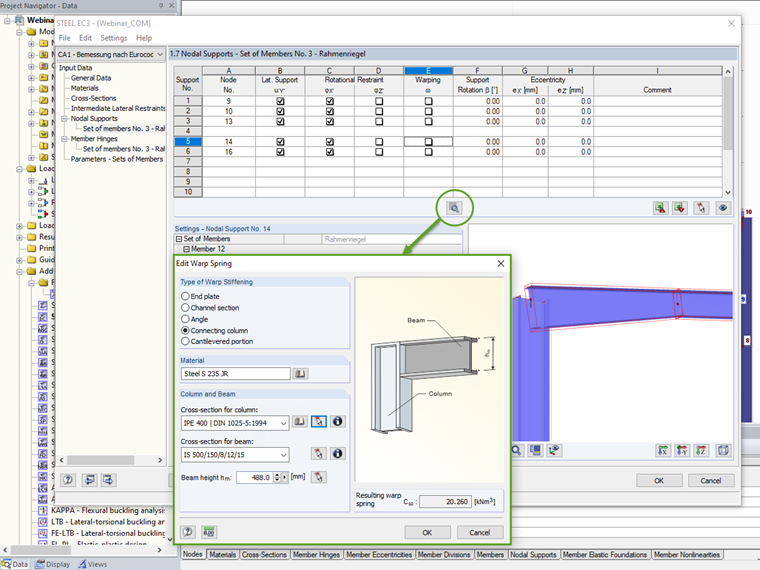
Pilar de conexão

Restrição de empenamento através do pilar de ligação

A restrição ao empenamento por um pilar ligado resulta da rigidez à torção da secção do pilar. O pré -requisito para a sua eficácia é a disposição dos reforços como uma extensão dos banzos no pilar.

Cω = G \cdot I_{T} \cdot h_{m}

C_ω	Wölbfeder
G	Schubmodul
I_T	Torsionsträgheitsmoment
h_m	Abstand der Flanschmittellinien

Mola de empenamento para restrição de empenamento através do pilar de ligação

Parte em consola

Restrição de empenamento através da viga em consola

C_{ω} = G \cdot I_{T} \cdot \frac{1}{λ} \cdot \tan h (λ \cdot l_{k})

C_ω	Wölbfeder
G	Schubmodul
I_T	Torsionsträgheitsmoment des überstehenden Trägers
λ	√[(G ⋅ I_T) / (E ⋅ I_ω)]
l_k	Überstandslänge
I_ω	Wölbwiderstand des überstehenden Trägers

Mola de empenamento para restrição de empenamento através da viga em consola

Base de dados de conhecimento

KB 000585 | Cálculo de molas de empenamento para consideração na análise de encurvadura por flexão-torção ...

Ligações

Software para o dimensionamento de estruturas de aço

Referências

Petersen, C. Statik und Stabilität der Baukonstruktionen, 2. ed.). Wiesbaden: Vieweg, 1982

;