Berechnung der Wölbfeder
Wird eine Wölbeinspannung angesetzt, so entspricht dies der vollständigen Behinderung der Querschnittsverwölbung beispielsweise über eine starre Stirnplatte. In der Realität ist diese volle Einspannung allerdings meist nicht gegeben, da die Stirnplatten nicht unendlich starr, sondern ebenfalls verformbar sind. Die Bemessungsmodule für den Stahl- und Aluminiumbau ermöglichen bei der Eingabe der Knotenlager eine direkte Berechnung der Wölbfedern aus den im Folgenden vorgestellten Varianten nach [1].
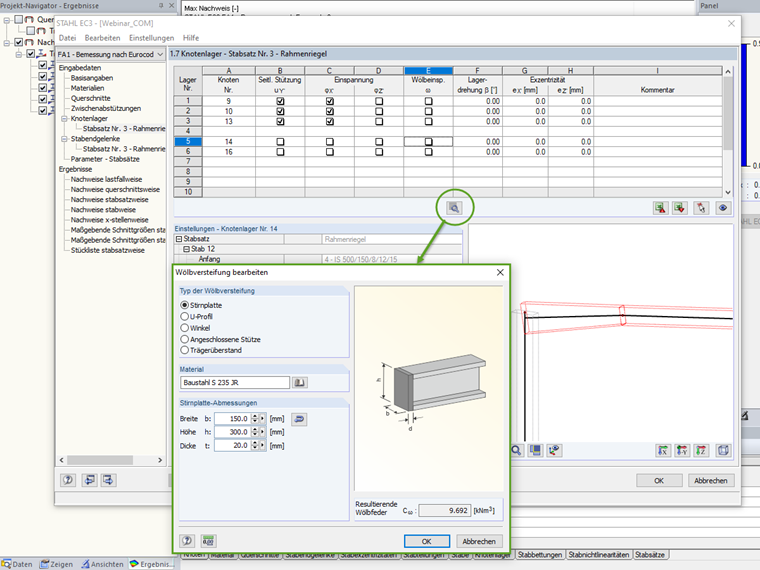
Stirnplatte
Die Wölbbehinderung der Stirnplatte ergibt sich aus der Drillsteifigkeit der angeschlossenen Platte.
|
Cω |
Wölbfeder |
|
G |
Schubmodul |
|
b |
Breite der Stirnplatte |
|
h |
Höhe der Stirnplatte |
|
t |
Dicke der Stirnplatte |
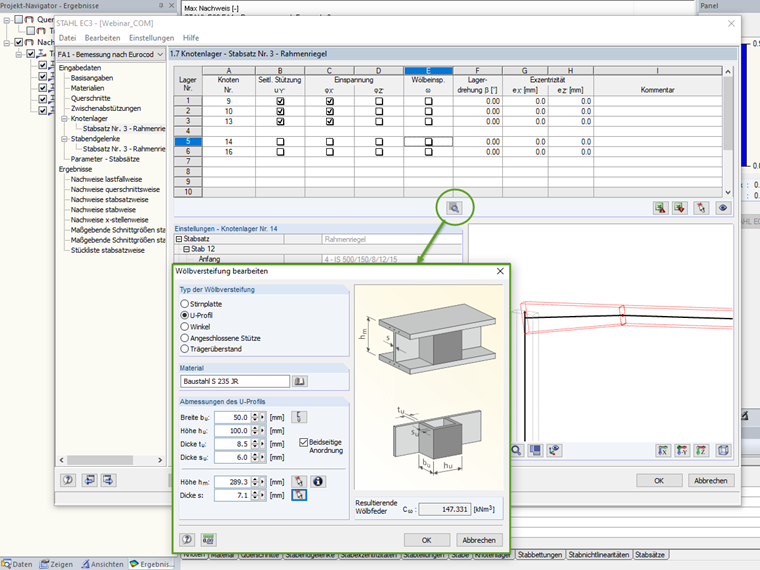
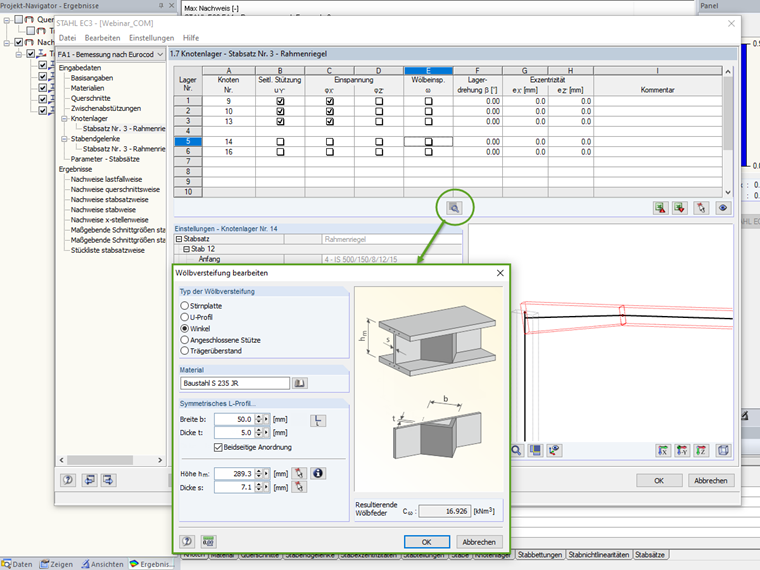
U-Profil und Winkelprofile
Die Wölbbehinderung durch drillsteife Querschotte ist aufgrund der höheren Torsionssteifigkeit wesentlich größer als durch Stirnplatten und Trägerüberstand. Einseitig eingeschweißte U- oder L-Steifen bilden zusammen mit dem Steg einen Hohlkasten, bei beiderseitiger Anordnung ergibt sich entsprechend ein Hohlkasten mit größeren Abmessungen.
|
Cω |
Wölbfeder |
|
G |
Schubmodul |
|
hm |
Abstand der Mittelebenen der Flansche des Trägers |
|
Am |
Von der Mittellinie eingeschlossene Fläche |
|
li |
Seitenlänge |
|
ti |
Blechdicke |
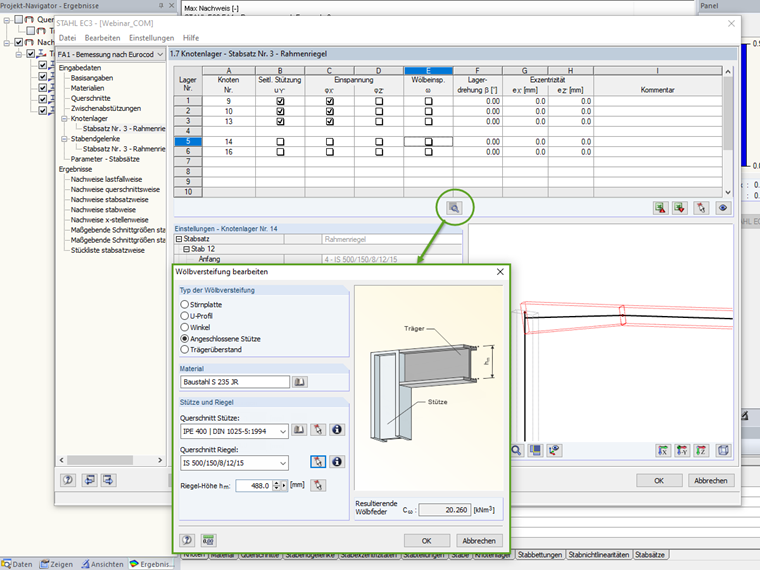
Angeschlossene Stütze
Die Wölbbehinderung durch eine angeschlossene Stütze ergibt sich aus der Torsionssteifigkeit des Stützenquerschnitts. Voraussetzung für dessen Wirksamkeit ist die Anordnung von Steifen als Verlängerung der Flansche in der Stütze.
|
Cω |
Wölbfeder |
|
G |
Schubmodul |
|
IT |
Torsionsträgheitsmoment |
|
hm |
Abstand der Flanschmittellinien |
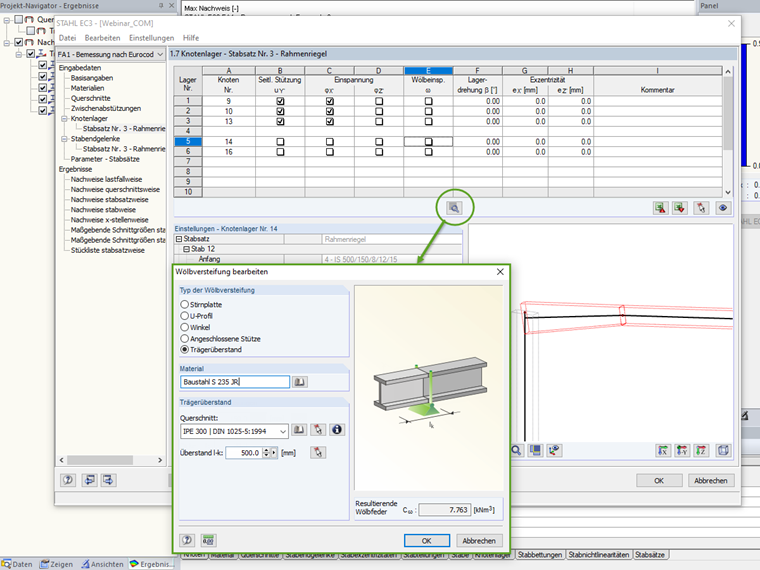
Trägerüberstand
|
Cω |
Wölbfeder |
|
G |
Schubmodul |
|
IT |
Torsionsträgheitsmoment des überstehenden Trägers |
|
λ |
√[(G ⋅ IT) / (E ⋅ Iω)] |
|
lk |
Überstandslänge |
|
Iω |
Wölbwiderstand des überstehenden Trägers |