Avaliação de formas próprias locais e globais com o RSBUCK para a determinação de comprimentos equivalentes de barras

Fundamentação teórica

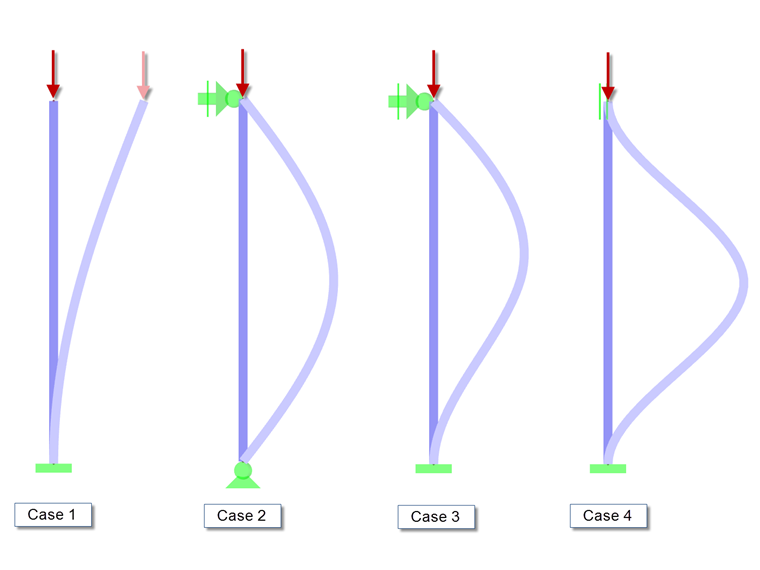
A esbelteza e os coeficientes de redução resultantes são determinados através da análise de encurvadura por flexão de acordo com a EN 1993-1-1, capítulo 6.3, tendo em consideração a carga de encurvadura elástica crítica N_cr. Esta carga crítica é determinada analiticamente no módulo adicional STEEL ‑ EC3 utilizando o comprimento efetivo determinante. Para estruturas simples, existem quatro casos de Euler comumente utilizados.

Casos Euler

No caso de estruturas complexas, a avaliação do comprimento efetivo não é tão trivial. Para esta determinação, pode utilizar o módulo adicional RSBUCK.

Um fator de carga crítico é primeiro determinado para a estrutura. Isto é multiplicado pelas forças normais das barras para obter as cargas críticas. Os comprimentos efetivos correspondentes para a encurvadura em torno dos dois eixos são calculados utilizando a fórmula ajustada: N_cr = E ∙ I ∙ π²/L_cr. Finalmente, os fatores de carga efetivos são determinados a partir desta relação: k_cr = L_cr/L.

Formas globais e locais no RSBUCK

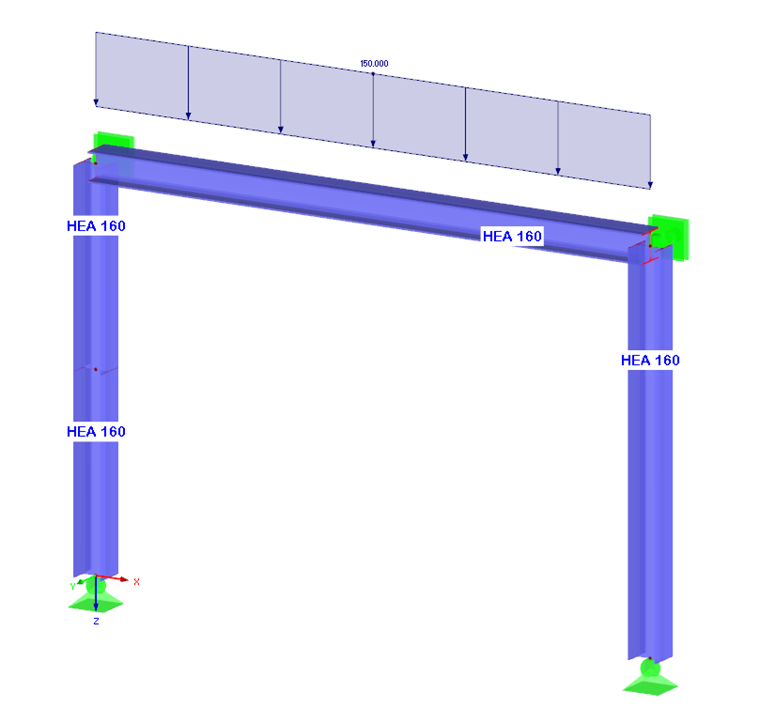
A determinação das formas próprias e a avaliação apropriada são explicadas com o seguinte exemplo de um pórtico simples.

Frame

Na determinação de um modo de encurvadura e comprimentos de encurvadura, a carga desempenha um papel importante: Os valores de encurvadura dependem não apenas do modelo estrutural, mas também da relação das forças normais com a carga crítica total de encurvadura N_cr. Os comprimentos efetivos podem ser calculados apenas para barras com forças de compressão. Além disso, a distribuição de carga por toda a estrutura afeta a determinação dos fatores críticos. Ao avaliar graficamente os modos individuais, pode identificar se existe um modo global ou local. Se existe uma carga crítica de uma barra individual no caso da carga crítica estrutural mais desfavorável, isto será evidente no gráfico. No caso de uma falha assim, os resultados não podem ser utilizados para todas as outras barras e não devem ser avaliados.

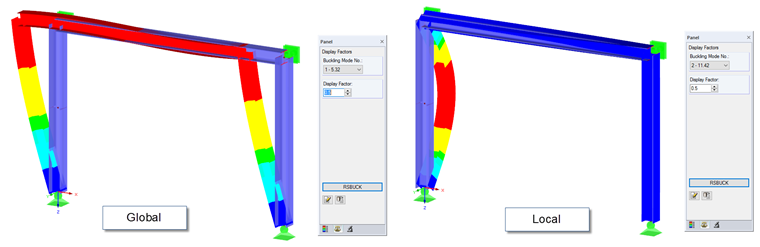
Em nosso exemplo, o primeiro modo de forma com o fator de carga crítico de 5,32 ilustra o deslocamento global do pórtico no plano do pórtico. A segunda forma modal, com o fator de carga crítico de 11,42, ilustra o deslocamento local do pilar esquerdo no plano do pórtico (encurvadura em torno do eixo menor z).

formas próprias

Barras divididas

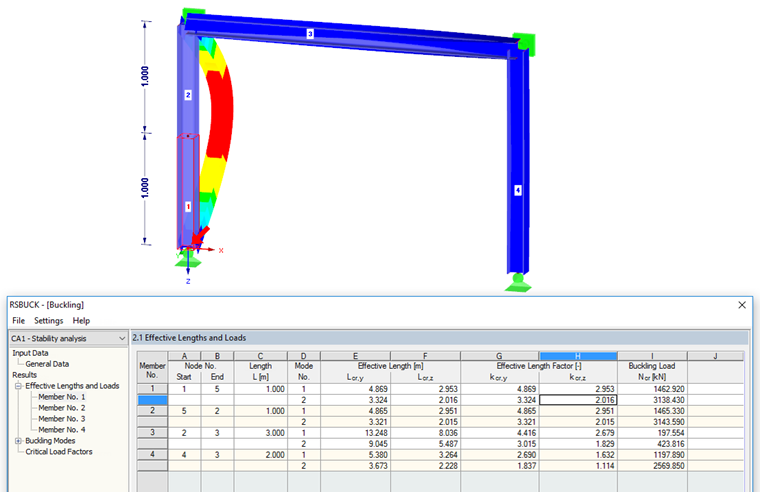
Ao calcular os comprimentos efetivos e os fatores de comprimento efetivo, é necessário considerar a divisão das barras. Neste exemplo, a coluna esquerda do pórtico é constituída por duas barras individuais. Por razões técnicas de modelação, o pilar foi dividido ao meio. Ao considerar apenas a forma do modo local (modo de encurvadura nº 2), esta pode ser classificada no caso nº 2 de Euler e no resultado esperado do fator de comprimento efetivo k_{cr, z} = 1,0. No entanto, a janela de resultados 2.1 no módulo adicional exibe o fator de comprimento efetivo k_{cr, z} = 2,0 para ambas as barras "parciais" do pilar.

Isto pode ser facilmente explicado pelas relações mencionadas acima, em "Fundamentos Teóricos". Neste caso, o comprimento de encurvadura para todo o pilar é igual ao comprimento do pilar e, portanto, o fator de comprimento efetivo é 1. Da in RSKNICK aber Einzelstäbe ausgewertet werden, ergibt sich aus k_cr = L_cr / L mit L = 0,5 ∙ Stützenlänge ein Knicklängenbeiwert von 2,0.

Os fatores de comprimento efetivo para barras contínuas não podem ser determinados diretamente no RSBUCK. Para fazer isso, é possível avaliar os resultados das barras individuais. A barra que prova a menor carga de encurvadura_Ncr pode ser considerada a barra individual determinante de uma barra contínua. Em seguida, pode calcular os_{valores de k cr a} partir do comprimento efetivo desta barra e do comprimento total da barra contínua.

Comprimentos de encurvadura