15037x

2017-12-12

Пример расчета жесткого на изгиб соединения лобовой пластины по норме EN 1993-1-8

В нашем примере необходимо определить несущую способность лобовой пластины по норме EN 1993-1-8 [1]; другие компоненты здесь не рассматриваются. Для оценки результатов были использованы размеры типового соединения IH 3.1 B 30 24 из литературы [2]. В примере используется материал S 235 и болты прочности 10.9.

Пример расчета

Определение значений рабочей длины

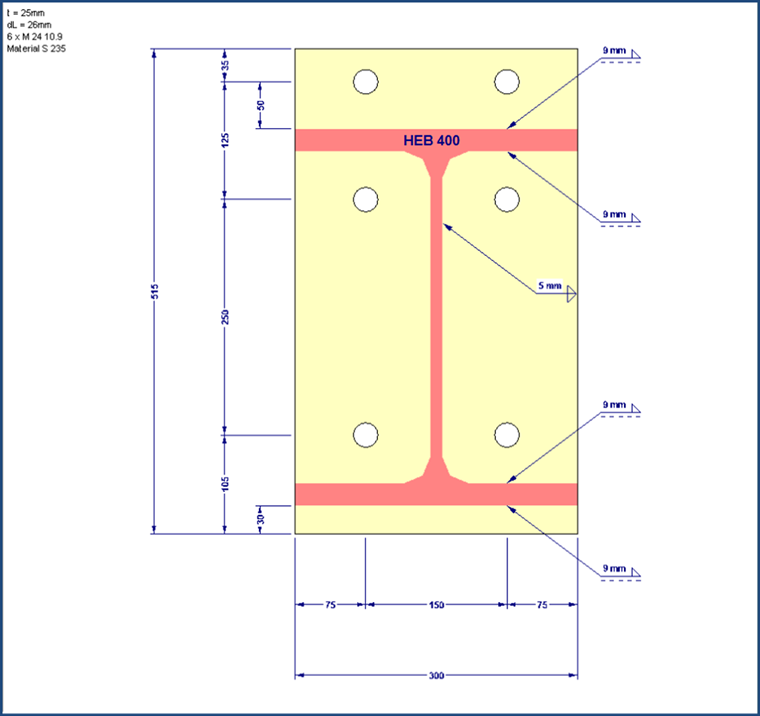
Сначала необходимо определить рабочие длины полок стойки по таблице 6.6. Нижний ряд болтов почти не влияет на сжатую полку из-за очень малого плеча силы, и поэтому не учитывается. Поскольку оба верхних ряда болтов разделены растянутой полкой балки, то эти ряды болтов должны рассматриваться по отдельности. Таким образом можно избежать выхода из работы группы рядов шурупов. Для расчета значений рабочих длин требуются параметры e, m, e_x, m_x, m₂, b_p, w.

Параметры для эффективной длины (Источник: [1])

В нашем примере были рассчитаны следующие значения:

\begin{array}{l} e = 75 mm \\ m = \frac{300 - 13, 5}{2} - 75 - 0, 8 \cdot 5 \cdot \sqrt{2} = 62, 6 mm \\ e_{x} = 35 mm \\ m_{x} = 50 - 0, 8 \cdot 9 \cdot \sqrt{2} = 39, 8 mm \\ m_{2} = 125 - 50 - 24 - 0, 8 \cdot 9 \cdot \sqrt{2} = 40, 8 mm \\ b_{p} = 300 mm \\ w = 150 mm \end{array}

Формула 1

У рабочих длин проводится различие между кругообразными и некругообразными шаблонами кривой текучести. Для линейного шаблона кривой текучести требуется значение α по рисунку 6.11. Вводные значения для этого основаны на отношениях плеча силы к стенке балки (λ₁) или к полке балки (λ₂) к общей ширине полки тавровой стойки. Значения α между двумя диаграммами на рисунке 6.11 можно линейно интерполировать.

\begin{array}{l} λ_{1} = \frac{62, 6}{62, 6 75} = 0, 45 \\ λ_{2} = \frac{40, 8}{62, 6 75} = 0, 30 \\ α \approx 6, 65 \end{array}

Формула 2

Определение значения α (Источник: [1])

С помощью данных вводных значений рабочие длины определяются по таблице 6.6 следующим образом.

Кругообразный шаблон линии текучести для внешнего ряда болтов:

l_{eff, cp, a} = \min \{\begin{matrix} 2 \cdot π \cdot 39, 8 \\ π \cdot 39, 8 150 \\ π \cdot 39, 8 2 \cdot 75 \end{matrix}\} = 250, 1 mm

Формула 3

Кругообразный шаблон линии текучести для внутреннего ряда болтов:
l_eff,cp,i = 2 ∙ π ∙ 62,6 = 393,3 мм

Некругообразный шаблон линии текучести для внешнего ряда болтов:

l_{eff, nc, a} = \min \{\begin{matrix} 4 \cdot 39, 8 1, 25 \cdot 35 \\ 75 2 \cdot 39, 8 0, 625 \cdot 35 \\ 0, 5 \cdot 300 \\ 0, 5 \cdot 150 2 \cdot 39, 8 0, 625 \cdot 35 \end{matrix}\} = 150, 0 mm

Формула 4

Некругообразный шаблон линии текучести для внутреннего ряда болтов:
l_eff,nc,i = 6,65 ∙ 62,6 = 416,3 мм

Для определения несущей способности в режиме выхода из работы 1, то есть с чистой текучестью полки, применяется более короткая длина у обоих шаблонов кривых текучести. При нахождении несущей способности в режиме выхода из работы 2, то есть выхода из работы болтов с одновременной текучестью полки, может применяться только некругообразный шаблон линии текучести.

Мы получим следующие значения рабочей длины.

Внешний ряд болтов:
l_eff,1,a = 150 мм
l_eff,2,a = 150 мм

Внутренний ряд болтов:
l_eff1,i = 393,3 мм
l_eff2,i = 416,3 мм

Проверка на возникновение опорных усилий.

Перед расчетом несущей способности лобовой пластины в режиме выхода их работы 1, необходимо проверить, могут ли возникать опорные усилия. Поскольку это позволяет достичь более высоких расчетных значений несущей способности, то размеры и толщину пакета зажимов всегда следует выбрать или задать таким образом, чтобы было выполнено условие L_b < L_b*. L_b - деформируемая длина болта, которая принята равной длине зажима (общая толщина пакета листов и подкладных шайб), плюс половина высоты головки и половина высоты гайки.

L_{b} * = \frac{8, 8 \cdot m^{3} \cdot A_{s}}{l_{eff 1} \cdot t_{f} ³}

Формула 5

Длина зажима при условии применения симметричного балочного соединения равна:
L_b = 2 ∙ 25 + 2 ∙ 4 + 0,5 ∙ 19 + 0,5 ∙ 15 = 75 мм

Значение L_b* должно быть найдено отдельно для внешнего и внутреннего ряда болтов.

Внешний ряд болтов:

L_{b} * = \frac{8, 8 \cdot 39, 8^{3} \cdot 353}{150 \cdot 25 ³} = 83, 6 mm

Формула 6

Внутренний ряд болтов:

L_{b} * = \frac{8, 8 \cdot 62, 6^{3} \cdot 353}{393, 3 \cdot 25 ³} = 124 mm

Формула 7

Таким образом, в обоих рядах болтов могут возникать опорные усилия.

Несущая способность полки тавровой стойки

Для режима выхода из работы «полная текучесть полки» в данном примере используется метод 1 по норме EN 1993-1-8. Прочность на растяжение у обоих полок тавровой стойки определяется следующим образом.

\begin{array}{l} F_{T, 1, Rd} = \frac{4 \cdot M_{pl, 1, Rd}}{m} \\ mit \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot l_{eff, 1} \cdot t_{f} ² \cdot f_{y}}{γ_{M 0}} \\ m = 39, 8 mm für die äußere Schraubenreihe \\ m = 62, 6 mm für die innere Schraubenreihe \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot 15, 0 \cdot 2, 52 \cdot 23, 5}{1, 0} = 550, 78 kNcm für die äußere Schraubenreihe \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot 39, 33 \cdot 2, 52 \cdot 23, 5}{1, 0} = 1.444, 15 kNcm für die innere Schraubenreihe \\ F_{T, 1, Rd} = \frac{4 \cdot 550, 78}{3, 98} = 553, 55 kN für die äußere Schraubenreihe \\ F_{T, 1, Rd} = \frac{4 \cdot 1.444, 15}{6, 26} = 922, 78 kN für die innere Schraubenreihe \end{array}

Формула 8

Режим выхода из работы «Выход из работы болта с достижением текучести полки»:

\begin{array}{l} F_{T, 2, Rd} = \frac{2 \cdot M_{pl, 2, Rd} n \cdot {ΣF}_{t, Rd}}{m n} \\ mit \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot l_{eff, 2} \cdot t_{f} ² \cdot f_{y}}{γ_{M 0}} \\ {ΣF}_{t, Rd} = ΣZugtragfähigkeiten der Schrauben \\ n = e_{\min} < 1, 25 \cdot m \\ e_{\min} = 35 mm für die äußere Schraubenreihe \\ e_{\min} = 75 mm für die innere Schraubenreihe \\ m = 39, 8 mm für die äußere Schraubenreihe \\ m = 62, 6 mm für die innere Schraubenreihe \\ {ΣF}_{t, Rd} = \frac{2 \cdot k_{2} \cdot f_{ub} \cdot A_{S}}{γ_{M 2}} = \frac{2 \cdot 0, 9 \cdot 100 \cdot 3, 53}{1, 25} = 508, 32 kN \\ Die Durchstanzkraft wurde überprüft, ist aber nicht maßgebend . \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot 15, 0 \cdot 2, 52 \cdot 23, 5}{1, 0} = 550, 78 kNcm für die äußere Schraubenreihe \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot 41, 63 \cdot 2, 52 \cdot 23, 5}{1, 0} = 1.528, 60 kNcm für die innere Schraubenreihe \\ F_{T, 2, Rd} = \frac{2 \cdot 550, 78 3, 5 \cdot 508, 32}{3, 98 3, 5} = 385, 12 kN für die äußere Schraubenreihe \\ F_{T, 2, Rd} = \frac{2 \cdot 1.528, 60 7, 5 \cdot 508, 32}{6, 26 7, 5} = 499, 24 kN für die innere Schraubenreihe \end{array}

Формула 9

Определяющая несущая способность полки тавровой стойки

Для обоих рядов болтов определяющим является режим выхода из работы 2.

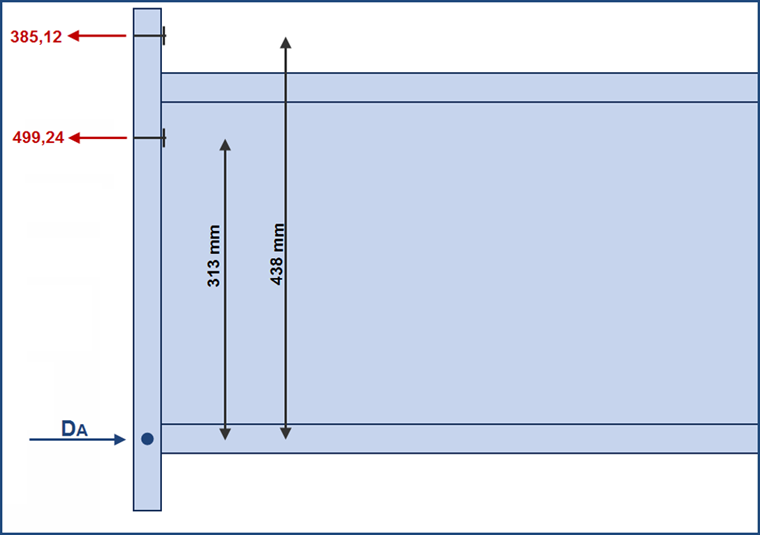
Внешний ряд болтов: 385,12 кН

Внутренний ряд болтов: 499,24 кН

Моментная прочность соединения

Полученные расчетные значения прочности отдельных рядов болтов теперь должны быть умножены на соответствующее плечо силы до точки сжатия.

Плечо силы равно
438 мм для внешнего ряда болтов,
313 мм для внутреннего ряда болтов.

Таким образом, расчетная моментная прочность соединения равна
M_Rd = 385,12 ∙ 0,438 + 499,24 ∙ 0,313 = 324,95 кНм.

Tragfähigkeiten der Schraubenreihen und zugehörige Hebelarme

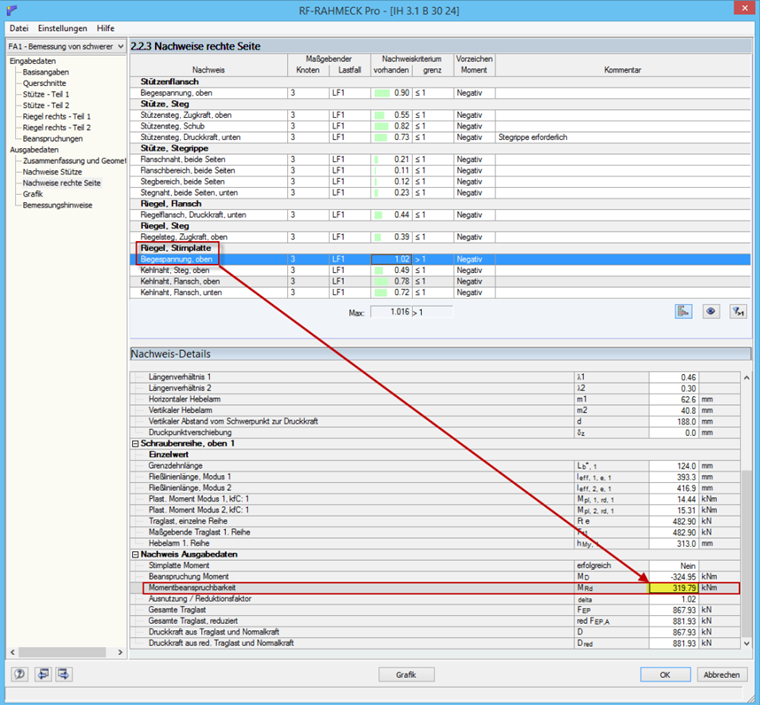
Сравнение результатов

Если выполнить расчет данного соединения в RF-/FRAME-JOINT Pro как для жесткого рамочного соединения, то расчетная прочность лобовой пластины составит 319,79 кНм. Согласно типовым соединениям [2], расчетная прочность составляет 331,3 кНм, что относительно точно соответствует расчету вручную.

Несущая способность в модуле RF-/FRAME-JOINT Pro

Автор

Г-н Фрёлих оказывает техническую поддержку нашим заказчикам и отвечает за разработки железобетонных конструкций.

Ссылки

Стальные соединения

Ссылки

Eurocode 3: Bemessung und Konstruktion von Stahlbauten - Teil 1-8: Bemessung von Anschlüssen; EN 1993-1-8:2005 + AC:2009
Weynand, K.; Oerder, R.: Typisierte Anschlüsse im Stahlhochbau nach DIN EN 1993-1-8. Düsseldorf: Stahlbau, 2013

Скачивания

Модель в программе RFEM

1,16 MB

У вас есть какие-нибудь вопросы?

События

2024-05-15

Онлайн-тренинги

Rfem 6 | Студенты | Основы расчёта стальных конструкций

2024-05-16

Вебинар

Учёт этапов строительства в RFEM 6

2024-11-06

Онлайн-тренинги

Rfem 6 | Студенты | Основы расчёта стальных конструкций

Видеоролики

Событие

Вебинар | Расчёт стальных стержней по норме AISC 360/341-22 в программе RFEM 6

Длина: 01:01:43 min

Событие

Вебинар | Соединения с круглыми пустотелыми профилями в RFEM 6

Длина: 00:00:00 min

Событие

Вебинар | RWIND 2 - Расчет ветровых нагрузок с помощью CFD Simulation

Длина: 00:00:00 min

Функции продукта

Коэффициент чувствительности

Длина: 00:00:32 min

Функции продукта

Компонент «Вырез пластины»

Длина: 00:00:53 min

Событие

Вебинар | Расчёт напряжений моделей лестниц в RFEM 6

Длина: 01:05:28 min

Функции продукта

Компонент «Вспомогательное тело»

Длина: 00:00:32 min

Функции продукта

Пластическая прочность с изменением касательных напряжений

Длина: 00:00:38 min

Событие

Вебинар | Основы анализа изменений во времени в программе RFEM 6

Длина: 00:00:00 min

Плейлист

Модели для скачивания

Модель 004864 | Steel Structure Connection | AISC 360-22

40x

Соединение стальной конструкции | AISC 360-22

Модель 004859 | Металлическая конструкция | AISC 360/341-22

231x

34x

Металлическая конструкция | AISC 360/341-22

3217x

214x

Стальная конструкция колонны

259x

Пешеходно-велосипедный мост в Айхсютте, Германия

Модель 004848 | Металлическая конструкция

303x

34x

Металлическая конструкция

365x

Подвесные стеллажи, Китай

477x

53x

Стальное соединение

296x

30x

Подъемная балка типа H

Стальной силос с ветровыми нагрузками | ASCE 7

289x

35x

Стальной силос с ветровыми нагрузками | ASCE 7

Статьи из базы знаний

Узнать больше

При расчете жестких на изгиб соединений двутавровых балок соединение разделяется на отдельные части. Для этих основных компонентов соединения существуют отдельные формулы для определения несущей способности и жесткости. В программах RFEM и RSTAB рамные соединения можно рассчитать с помощью дополнительного модуля RF-/FRAME-JOINT Pro.

Узнать больше

КБ 001875 | Расчет стержней, устойчивых к моменту, по норме AISC 341-22 в программе RFEM 6

В аддоне Расчёт стальных конструкций для RFEM 6 доступны три типа рам (обычные, промежуточные и специальные). Результат сейсмического расчета по AISC 341-22 подразделяется на две части: требования к стержням и требования к соединениям.

Узнать больше

Аддон Расчёт стальных конструкций в RFEM 6 теперь содержит функцию выполнения сейсмического расчёта по нормам AISC 341-16 и AISC 341-22. В настоящее время в нем содержится пять типов сейсмоустойчивых систем (SFRS).

Узнать больше

Функции продуктов

Характерная для 002807 | Представление 3D результатов МКЭ

В диалоговом окне «Querschnittпечать,

Узнать больше

Расчёт стальных конструкций | Обзор расчета сейсмических устойчивых систем

Расчет пяти типов сейсмоустойчивых систем (SFRS): )
Проверка пластичности соотношений ширины и толщины для стенок и полок
Расчет требуемой прочности и жесткости для связей устойчивости балок
Расчет максимального шага для связей устойчивости балок
Расчет требуемой прочности в местах расположения шарниров для усиления устойчивости балок
Расчет требуемой прочности колонны с возможностью пренебрежения всеми изгибающими моментами, сдвигом и кручением для предельного состояния сверхпрочности
Расчётная проверка коэффициентов гибкости колонн и связей

Узнать больше

Сейсмика в аддоне Расчёт стальных конструкций | Результаты

Результаты сейсмического расчета можно разделить на две части: требования к стержням и требования к соединениям.

«Сейсмические требования» включают в себя Требуемую прочность на изгиб и Требуемую прочность на сдвиг соединения балка-колонна для рам, устойчивых к моменту. Они перечислены в закладке «Соединение рам, устойчивых к моменту, по стержням». Для усиленных рам Требуемая прочность соединения на растяжение и Требуемая прочность соединения на сжатие указаны во вкладке «Соединение связи по стержням».

Программа отображает выполненные расчётные проверки в таблицах. В подробностях расчёта четко отображаются формулы и ссылки на норматив.

Узнать больше

Характерная для 002733 | Сейсмический расчет стальных стержней по норме AISC 341-16

В дополнении Расчёт железобетонных конструкций предоставляет возможность выполнить сейсмический расчёт по AISC 341-16 для стальных стержней.

Для этого в программе имеется пять типов SFRS (сейсмоустойчивые системы).

Подробнее

Узнать больше

Часто задаваемые вопросы (FAQ)

Как задать пластический шарнир в RFEM 6?

Каким образом можно обмениваться данными между RFEM 6 / RSTAB 9 и IDEA StatiCa?

Как с помощью ячеек в RFEM 6 или RSTAB 9 создать нагрузку на площадь на стержни?

В аддоне Расчёт стальных конструкций я установил граничные условия так, чтобы полка двутавровой балки была закреплена от горизонтального перемещения. Затем я рассчитал коэффициенты критической нагрузки с помощью аддона Устойчивость конструкции, но это не повлияло на значение коэффициента критической нагрузки. В чём причина?

Могу ли я оценить, какие минимальные сечения мне следует использовать, прежде чем приступить к проектированию моей модели?

Как задать трубку в качестве шпонки, работающей на срез в дополнительном модуле RF-/JOINTS Steel - Column Base?

Проекты заказчиков

Освещенный пункт взимания оплаты | © г-н Yungchao Ding, Jiangsu Jingong Space Structure Co., Ltd.

Пункт взимания оплаты Dawall в городе Шэньси, Китай

RFEM модель высокостеллажного склада с результатами деформаций

Подвесные стеллажи, Китай

Мультиэнергетическая станция (© GH HERVOUET)

Мультиэнергетическая станция в Ле Сабль-д'Олонн, Франция

Вид спереди на офисное здание с V-образными стальными составными колоннами | © Tragwerker GmbH

Офисное здание с интегрированным центром для посетителей и гаражом в Гайзельбулахе, Германия

Металлическая пергола в Университете Рафаэля Ландивара (© Ing. Enrique de León)

Стальная пергола на Plaza del Edificio L, Университет Рафаэль Ландивар, Гватемала

La Torre Radar a la izquierda (© SAQQARA Ingeniería)

Расчёт конструкции радарной башни в аэропорту Малаги, Испания

CP 001290 | Кровля амфитеатра театра в Мосте | © Carl Stahl & spol. s.r.o.

Амфитеатр городского театра в г. Мост, Чехия

CP 001287 | Вольер для птиц в Пражском зоопарке | © Carl Stahl & spol. s.r.o.

Птичий вольер в Пражском зоопарке, Чехия

Контейнерная конструкция с большим ситом | © Modular Structural Consultants LLC

Контейнерная конструкция на въезде в автомобильный анклав в Тампе, штат Флорида, США

Рекомендуемые продукты

RFEM 6 | Основная программа RFEM 6

RFEM 6

Основная программа

Новое поколение программного обеспечения 3D МКЭ предназначено для расчёта стержней, поверхностей и тел.

Цена первой лицензии 4 170,00 USD

RFEM 6 | Расчёт

Аддон Расчёт стальных конструкций для RFEM 6

Дополнение

Аддон Расчёт стальных конструкций выполняет расчёт стальных стержней по предельным состояниям по несущей способности и пригодности к эксплуатации в соответствии с различными нормативами.

Цена первой лицензии 2 550,00 USD

RFEM 6 | Узловые соединения

Стальные соединения для RFEM 6

Дополнение

Аддон Стальные соединения для RFEM позволяет рассчитывать стальные соединения с помощью модели КЭ. Моделирование выполняется автоматически в фоновом режиме, и им можно управлять с помощью простого и привычного ввода компонентов.

Цена первой лицензии 2 110,00 USD