Berechnungsbeispiel eines biegesteifen Stirnplattenanschlusses nach EN 1993-1-8

Berechnungsbeispiel

Ermittlung der effektiven Längen

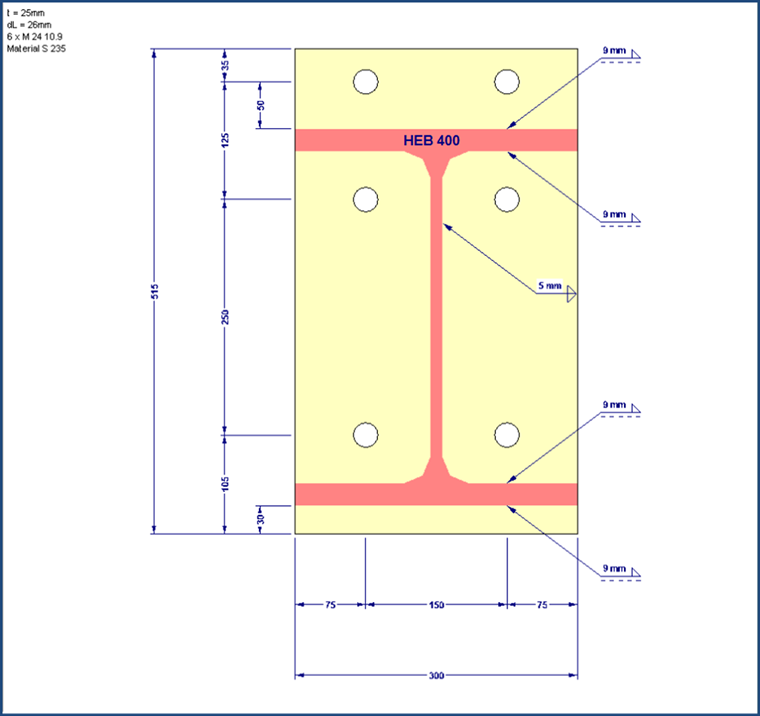
Zunächst müssen die effektiven Längen der Stummelflansche gemäß Tabelle 6.6 ermittelt werden. Die unterste Schraubenreihe trägt infolge des sehr geringen Hebelarmes zum Druckflansch kaum etwas bei und wird daher vernachlässigt. Da die beiden oberen Schraubenreihen durch den Trägerzugflansch geteilt sind, müssen hierbei nur die Schraubenreihen einzeln betrachtet werden. Ein Gruppenversagen der Schraubenreihen kann daher nicht auftreten. Für die Berechnung der effektiven Längen benötigt man die Parameter e, m, e_x, m_x, m₂, b_p, w.

Parameter für effektive Längen (Quelle: [1])

In diesem Beispiel ergeben sich folgende Werte:

Bei den wirksamen Längen wird zwischen kreisförmigem und nicht-kreisförmigem Fließlinienmuster unterschieden. Für das lineare Fließlinienmuster wird der Wert α aus Bild 6.11 benötigt. Als Eingangswerte dafür werden die Verhältnisse der Hebelarme zum Trägersteg (λ₁) beziehungsweise zum Trägerflansch (λ₂) zur Gesamtbreite des T-Stummelflansches benötigt. Die Werte für α zwischen zwei Diagrammen in Bild 6.11 dürfen linear interpoliert werden.

Ermittlung α-Wert (Quelle: [1])

Mit diesen Eingangswerten ermitteln sich die effektiven Längen nach Tabelle 6.6 wie folgt.

Kreisförmiges Fließlinienmuster für die äußere Schraubenreihe:

Kreisförmiges Fließlinienmuster für die innere Schraubenreihe:
l_eff,cp,i = 2 ∙ π ∙ 62,6 = 393,3 mm

Nicht kreisförmiges Fließlinienmuster für die äußere Schraubenreihe:

Nicht kreisförmiges Fließlinienmuster für die innere Schraubenreihe:
l_eff,nc,i = 6,65 ∙ 62,6 = 416,3 mm

Für die Ermittlung der Tragfähigkeit im Versagensmodus 1, also bei reinem Flanschfließen, wird die geringere Länge beider Fließlinienmuster angesetzt. Bei der Ermittlung der Tragfähigkeit im Versagensmodus 2, also Schraubenversagen mit gleichzeitigem Flanschfließen, kann nur ein nicht kreisförmiges Fließlinienmuster auftreten.

Somit ergeben sich folgende effektiven Längen.

Äußere Schraubenreihe:
l_eff,1,a = 150 mm
l_eff,2,a = 150 mm

Innere Schraubenreihe:
l_eff1,i = 393,3 mm
l_eff2,i = 416,3 mm

Überprüfung, ob Abstützkräfte auftreten können

Bevor die Tragfähigkeit der Stirnplatte im Versagensmodus 1 ermittelt wird, muss überprüft werden, ob sich Abstützkräfte einstellen können. Da sich damit wesentlich höhere Tragfähigkeiten erzielen lassen, sollten die Abmessungen und die Dicke des Klemmpakets stets so gewählt beziehungsweise verändert werden, dass die Gleichung L_b < L_b* erfüllt wird. Dabei ist L_b die Dehnlänge der Schraube, angesetzt mit der gesamten Klemmlänge (Gesamtdicke des Blechpakets und der Unterlegscheiben), plus der halben Kopfhöhe und der halben Mutternhöhe.

Die Klemmlänge ergibt sich in diesem Beispiel unter der Annahme, dass ein symmetrischer Trägerstoß angewandt wird, zu:
L_b = 2 ∙ 25 + 2 ∙ 4 + 0,5 ∙ 19 + 0,5 ∙ 15 = 75 mm

L_b* muss separat für die äußere und innere Schraubenreihe ermittelt werden.

Äußere Schraubenreihe:

Innere Schraubenreihe:

In beiden Schraubenreihen können somit Abstützkräfte auftreten.

Tragfähigkeit der T-Stummelflansche

Für den Versagensmodus "Vollständiges Fließen des Flansches" wird in diesem Beispiel das Verfahren 1 der EN 1993-1-8 angewandt. Dabei wird die Zugtragfähigkeit beider T-Stummelflansche wie folgt ermittelt.

Versagensmodus "Schraubenversagen mit gleichzeitigem Flanschfließen":

Maßgebende Tragfähigkeit der T-Stummelflansche

Für beide Schraubenreihen wird der Versagensmodus 2 maßgebend.

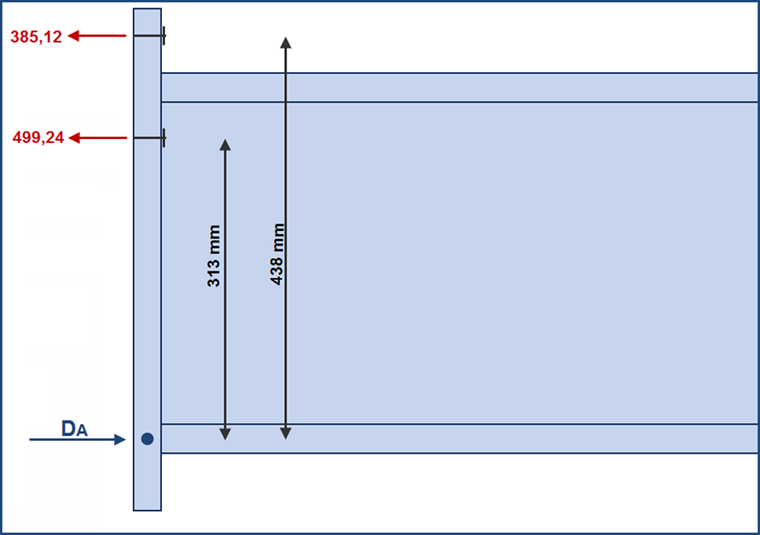
Äußere Schraubenreihe: 385,12 kN

Innere Schraubenreihe: 499,24 kN

Momententragfähigkeit des Anschlusses

Die ermittelten Tragfähigkeiten der einzelnen Schraubenreihen müssen nun nur noch mit dem jeweiligen Helbelarm zum Druckpunkt multipliziert werden.

Die Hebelarme betragen
438 mm für die äußere Schraubenreihe,
313 mm für die innere Schraubenreihe.

Somit ergibt sich die Tragfähigkeit des Anschlusses zu
M_Rd = 385,12 ∙ 0,438 + 499,24 ∙ 0,313 = 324,95 kNm.

Tragfähigkeiten der Schraubenreihen und zugehörige Hebelarme

Vergleich der Ergebnisse

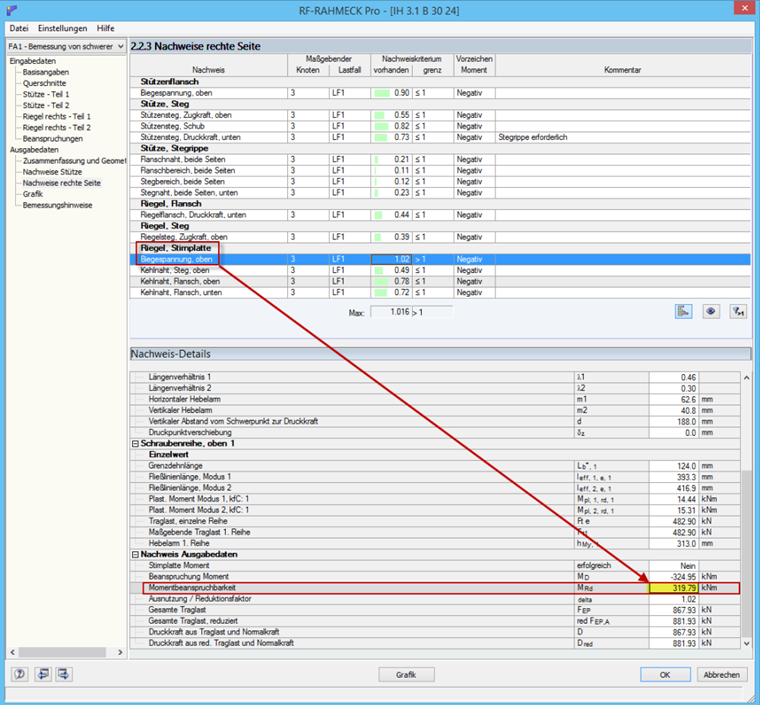
Berechnet man diesen Anschluss als biegesteife Rahmenecke in RF-/RAHMECK Pro, so erhält man dort eine Tragfähigkeit der Stirnplatte von 319,79 kNm. Laut den Typisierten Anschlüssen [2] beträgt die Tragfähigkeit 331,3 kNm, was relativ genau mit der Handrechnung übereinstimmt.

Tragfähigkeit in RF-/RAHMECK Pro