按照欧洲钢结构规范 EN 1993-1-8 计算端板刚性连接示例

计算举例

确定有效长度

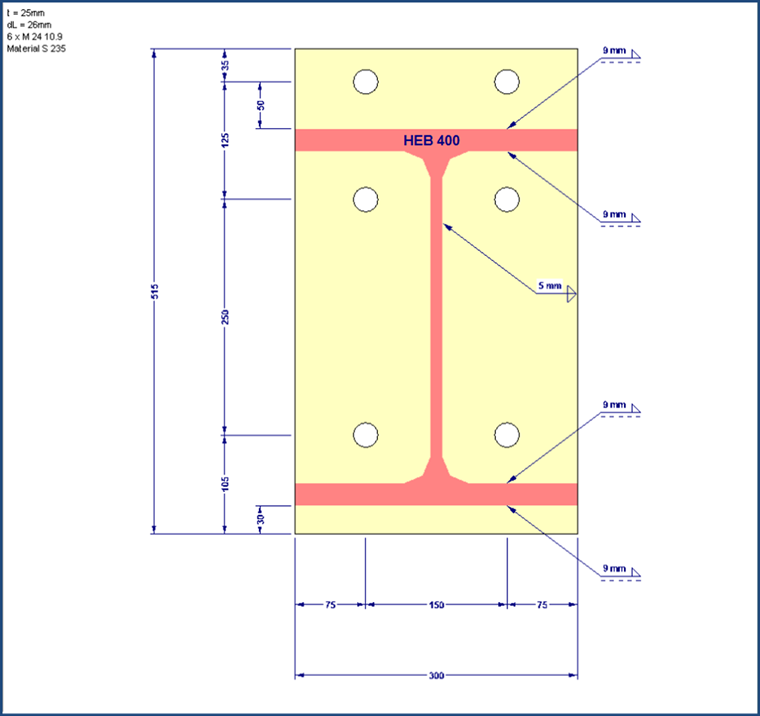
首先，必须按照表 6.6 确定短接翼缘的有效长度。 由于杠杆臂很小，所以底部的螺栓排对受压翼缘几乎没有影响，因此可以忽略。 由于上部的两排螺栓排都被梁的受拉翼缘分隔，所以螺栓排只能单独考虑。 这样可以避免螺栓排的组失效。 计算有效长度需要参数 e、m、ex、m_x 、m₂ 、b_p 、w。

有效长度参数（来源： [1]）

对于本例，已经计算了以下值：

在计算有效长度时，屈服线分为圆形和非圆形。 线性屈服线模式需要图 6.11 中的 α 值。 对此的输入值基于杠杆臂与梁腹板（λ₁ ）或梁翼缘（λ₂ ）与T形翼缘总宽度之间的关系。 图 6.11 中两个图表之间的α值可以线性插值。

确定α值（资料来源： [1]）

使用这些输入值可以按照表 6.6 确定有效长度。

外部螺栓行的圆形屈服线模式：

内部螺栓行的圆形屈服线模式：
l_eff,cp,i = 2 ∙ π ∙ 62,6 = 393,3 mm

外部螺栓行的非圆形屈服线模式：

内部螺栓行的非圆形屈服线模式：
l_eff,nc,i = 6.65 ∙ 62.6 = 416.3 mm

为了确定失效模式 1 （即纯翼缘屈服）下的设计承载力，使用两种屈服线模式中较短的长度。 在计算失效模式 2 下的设计承载力时，即螺栓失效同时翼缘屈服时，只能出现非圆形屈服线模式。

由此得出以下有效长度。

外部螺栓行:
l_eff,1,a = 150 mm
l_eff,2,a = 150 mm

内部螺栓行:
l_eff1,i = 393,3 mm
l_eff2,i = 416,3 mm

检查是否会产生撬力

在确定失效模式 1 下端板的设计承载力之前，必须检查是否会产生撬力。 因为这可以实现更高的设计承载力值，所以在选择或更改握把包的尺寸和厚度时，应满足公式_Lb <_Lb * 的要求。 _Lb是螺栓的延伸长度，取等于抓握长度（材料和垫圈的总厚度）加上螺栓头高度和螺母高度之和的一半。

假设应用对称梁节点，则夹点长度为：
L_b = 2 ∙ 25 + 2 ∙ 4 + 0.5 ∙ 19 + 0.5 ∙ 15 = 75 mm

对于外部和内部的螺栓排，L_b * 必须分别计算。

外部螺栓行:

内部螺栓行:

因此在两排螺栓中都会产生撬力。

T 形翼缘截面承载力设计值

对于“翼缘完全屈服”的失效模式，在这个例子中使用了 EN 1993-1-8 中的方法 1。 两个 T 形翼缘的抗拉承载力按下式计算。

“螺栓失效与翼缘屈服”失效模式：

控制 T 形翼缘的设计承载力

两排螺栓均采用失效模式 2 主导。

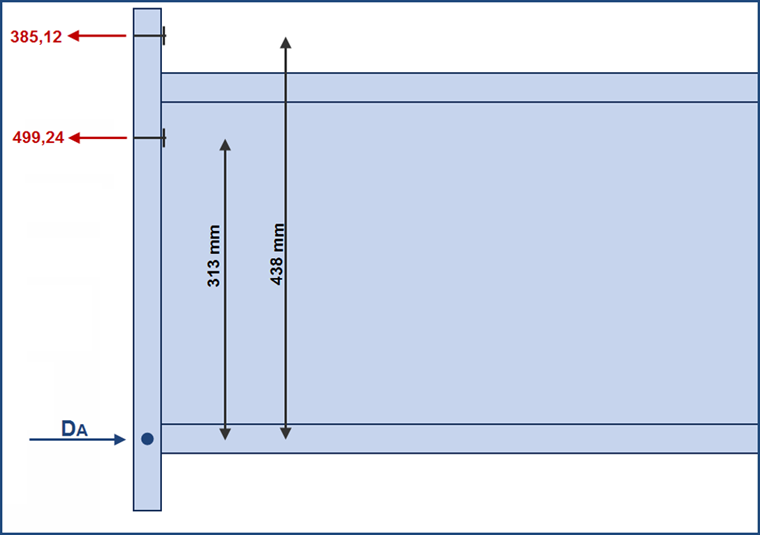
外部螺栓行: 385.12 kN

内部螺栓行: 499,24 kN

节点弯矩承载力

现在只需将计算得出的单个螺栓排的设计承载力值乘以相应的杠杆臂直到受压点。

杠杆臂是
438 mm 外部螺栓排
内部的螺栓排为313 mm。

计算的节点抗弯承载力为
M_Rd = 385.12 ∙ 0.438 + 499.24 ∙ 0.313 = 324.95 kNm。

Tragfähigkeiten der Schraubenreihen und zugehörige Hebelarme

结果比较

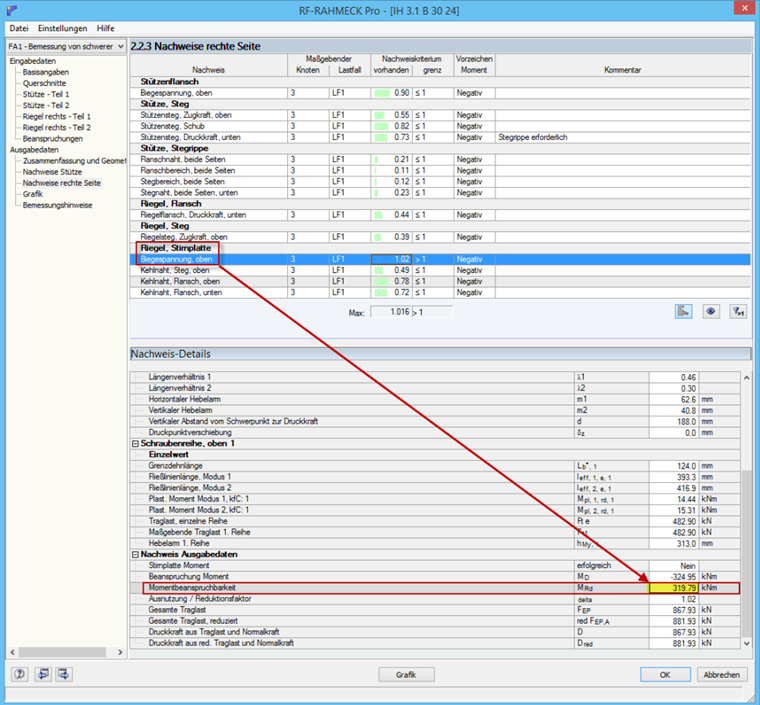
如果在 RF-/FRAME-JOINT Pro 中将此节点作为刚架节点计算，则端部板的设计承载力为 319,79 kNm。 根据典型连接[2] ，设计承载力为 331,3 kNm，与手动计算相对准确。

RF-/FRAME-JOINT Pro中的极限状态