17204x

001497

mgr inż. (FH) Walter Fröhlich

2017-12-12

Przykład obliczeń połączenia ze sztywną blachą doczołową zgodnie z EN 1993-1-8

W tym przykładzie należy określić nośność obliczeniową blachy czołowej zgodnie z EN 1993-1-8 [1]; pozostałe elementy nie są tutaj opisane. Für die Kontrolle der Ergebnisse wurden die Abmessungen des Anschlusses IH 3.1 B 30 24 der Typisierten Anschlüsse [2] verwendet. Als Material wird S 235 verwendet und Schrauben mit der Festigkeit 10.9.

Przykład obliczeń

Określanie długości efektywnych

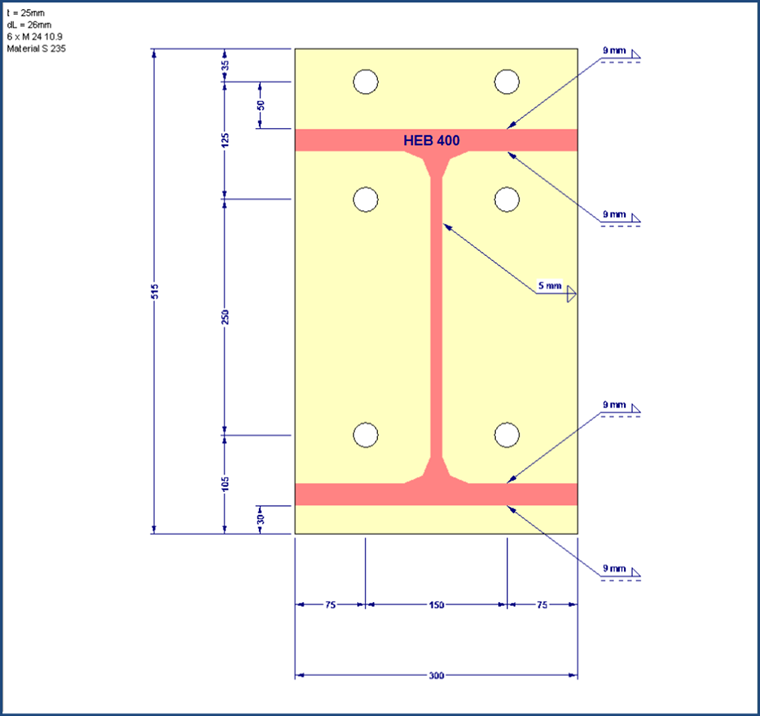
Najpierw należy określić długości efektywne króćców zgodnie z tabelą 6.6. Dolny rząd śrub ma niewielki wpływ na pas ściskany ze względu na bardzo małe ramię dźwigni i dlatego jest pomijany. Ponieważ oba górne rzędy śrub są podzielone przez rozciągany pas belki, rzędy śrub należy rozpatrywać tylko oddzielnie. W ten sposób można uniknąć uszkodzenia grupowego rzędów śrub. Do obliczenia długości efektywnych wymagane są parametry e, m, ex, m_x , m₂ ,_bp , w.

Parametry dla długości efektywnych (Źródło: [1])

Dla tego przykładu obliczono następujące wartości:

\begin{array}{l} e = 75 mm \\ m = \frac{300 - 13, 5}{2} - 75 - 0, 8 \cdot 5 \cdot \sqrt{2} = 62, 6 mm \\ e_{x} = 35 mm \\ m_{x} = 50 - 0, 8 \cdot 9 \cdot \sqrt{2} = 39, 8 mm \\ m_{2} = 125 - 50 - 24 - 0, 8 \cdot 9 \cdot \sqrt{2} = 40, 8 mm \\ b_{p} = 300 mm \\ w = 150 mm \end{array}

Wzór 1

W przypadku długości efektywnych rozróżnia się kołowy i niekołowy układ linii załomów. Liniowy przebieg linii załomów wymaga wartości α z Rysunku 6.11. Wartości wejściowe są oparte na stosunku ramion dźwigni do środnika dźwigara (λ₁ ) lub do pasa (λ₂ ) do całkowitej szerokości pasa króćca teowego. Wartości α pomiędzy dwoma wykresami na rysunku 6.11 mogą być interpolowane liniowo.

\begin{array}{l} λ_{1} = \frac{62, 6}{62, 6 75} = 0, 45 \\ λ_{2} = \frac{40, 8}{62, 6 75} = 0, 30 \\ α \approx 6, 65 \end{array}

Wzór 2

Określenie wartości α (Źródło: [1])

Korzystając z tych wartości wejściowych, długości efektywne są określane zgodnie z tabelą 6.6 w następujący sposób.

Okrągły układ linii załomów dla zewnętrznego rzędu śrub:

l_{eff, cp, a} = \min \{\begin{matrix} 2 \cdot π \cdot 39, 8 \\ π \cdot 39, 8 150 \\ π \cdot 39, 8 2 \cdot 75 \end{matrix}\} = 250, 1 mm

Wzór 3

Okrągły układ linii załomów dla wewnętrznego rzędu śrub:
l_eff,cp,i = 2 ∙ π ∙ 62,6 = 393,3 mm

Niekołowy układ linii załomów dla zewnętrznego rzędu śrub:

l_{eff, nc, a} = \min \{\begin{matrix} 4 \cdot 39, 8 1, 25 \cdot 35 \\ 75 2 \cdot 39, 8 0, 625 \cdot 35 \\ 0, 5 \cdot 300 \\ 0, 5 \cdot 150 2 \cdot 39, 8 0, 625 \cdot 35 \end{matrix}\} = 150, 0 mm

Wzór 4

Niekołowy układ linii załomów dla wewnętrznego rzędu śrub:
l_eff,nc,i = 6,65 ∙ 62,6 = 416,3 mm

Do określenia nośności obliczeniowej w trybie zniszczenia 1, tj. przy uplastycznieniu samego pasa, używana jest krótsza długość obu układów linii załomów. Podczas określania nośności obliczeniowej w trybie zniszczenia 2, tj. zniszczeniu śrub z równoczesnym uplastycznieniem pasa, może wystąpić tylko niekołowy układ linii załomów.

Daje to następujące długości efektywne.

Zewnętrzny rząd śrub:
l_eff,1,a = 150 mm
l_eff,2,a = 150 mm

Wewnętrzny rząd śrub:
l_eff1,i = 393,3 mm
l_eff2,i = 416,3 mm

Sprawdź, czy mogą powstać siły podważające

Przed określeniem nośności obliczeniowej płyty czołowej w trybie zniszczenia 1 należy sprawdzić, czy nie mogą wystąpić siły wyważające. Ponieważ pozwala to na osiągnięcie wyższych wartości nośności obliczeniowej, wymiary i grubość pakietu uchwytów należy zawsze dobierać lub zmieniać w taki sposób, aby spełnione było równanie L_b < L_b *. L_b jest długością wydłużenia śruby, przyjętą jako równą długości uchwytu (całkowita grubość materiału i podkładek) plus połowa sumy wysokości łba śruby i nakrętki.

L_{b} * = \frac{8, 8 \cdot m^{3} \cdot A_{s}}{l_{eff 1} \cdot t_{f} ³}

Wzór 5

Długość uchwytu, przy założeniu zastosowania symetrycznego połączenia belek, powoduje:
L_b = 2 ∙ 25 + 2 ∙ 4 + 0,5 ∙ 19 + 0,5 ∙ 15 = 75 mm

L_b * należy określić osobno dla zewnętrznego i wewnętrznego rzędu śrub.

Zewnętrzny rząd śrub:

L_{b} * = \frac{8, 8 \cdot 39, 8^{3} \cdot 353}{150 \cdot 25 ³} = 83, 6 mm

Wzór 6

Wewnętrzny rząd śrub:

L_{b} * = \frac{8, 8 \cdot 62, 6^{3} \cdot 353}{393, 3 \cdot 25 ³} = 124 mm

Wzór 7

W związku z tym w obu rzędach śrub mogą powstawać siły podważające.

Nośność obliczeniowa kołnierzy króćca teowego

W przypadku modelu zniszczenia „całkowite uplastycznienie pasa”, w tym przykładzie zastosowano metodę 1 zgodnie z EN 1993-1-8. Nośność przy rozciąganiu obu pasów króćców teowych jest określana w następujący sposób.

\begin{array}{l} F_{T, 1, Rd} = \frac{4 \cdot M_{pl, 1, Rd}}{m} \\ mit \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot l_{eff, 1} \cdot t_{f} ² \cdot f_{y}}{γ_{M 0}} \\ m = 39, 8 mm für die äußere Schraubenreihe \\ m = 62, 6 mm für die innere Schraubenreihe \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot 15, 0 \cdot 2, 52 \cdot 23, 5}{1, 0} = 550, 78 kNcm für die äußere Schraubenreihe \\ M_{pl, 1, Rd} = \frac{0, 25 \cdot 39, 33 \cdot 2, 52 \cdot 23, 5}{1, 0} = 1.444, 15 kNcm für die innere Schraubenreihe \\ F_{T, 1, Rd} = \frac{4 \cdot 550, 78}{3, 98} = 553, 55 kN für die äußere Schraubenreihe \\ F_{T, 1, Rd} = \frac{4 \cdot 1.444, 15}{6, 26} = 922, 78 kN für die innere Schraubenreihe \end{array}

Wzór 8

Tryb zniszczenia "Zniszczenie śruby z uplastycznieniem pasa":

\begin{array}{l} F_{T, 2, Rd} = \frac{2 \cdot M_{pl, 2, Rd} n \cdot {ΣF}_{t, Rd}}{m n} \\ mit \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot l_{eff, 2} \cdot t_{f} ² \cdot f_{y}}{γ_{M 0}} \\ {ΣF}_{t, Rd} = ΣZugtragfähigkeiten der Schrauben \\ n = e_{\min} < 1, 25 \cdot m \\ e_{\min} = 35 mm für die äußere Schraubenreihe \\ e_{\min} = 75 mm für die innere Schraubenreihe \\ m = 39, 8 mm für die äußere Schraubenreihe \\ m = 62, 6 mm für die innere Schraubenreihe \\ {ΣF}_{t, Rd} = \frac{2 \cdot k_{2} \cdot f_{ub} \cdot A_{S}}{γ_{M 2}} = \frac{2 \cdot 0, 9 \cdot 100 \cdot 3, 53}{1, 25} = 508, 32 kN \\ Die Durchstanzkraft wurde überprüft, ist aber nicht maßgebend . \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot 15, 0 \cdot 2, 52 \cdot 23, 5}{1, 0} = 550, 78 kNcm für die äußere Schraubenreihe \\ M_{pl, 2, Rd} = \frac{0, 25 \cdot 41, 63 \cdot 2, 52 \cdot 23, 5}{1, 0} = 1.528, 60 kNcm für die innere Schraubenreihe \\ F_{T, 2, Rd} = \frac{2 \cdot 550, 78 3, 5 \cdot 508, 32}{3, 98 3, 5} = 385, 12 kN für die äußere Schraubenreihe \\ F_{T, 2, Rd} = \frac{2 \cdot 1.528, 60 7, 5 \cdot 508, 32}{6, 26 7, 5} = 499, 24 kN für die innere Schraubenreihe \end{array}

Wzór 9

Określanie nośności obliczeniowej pasów króćca teowego

Tryb zniszczenia 2 dotyczy obu rzędów śrub.

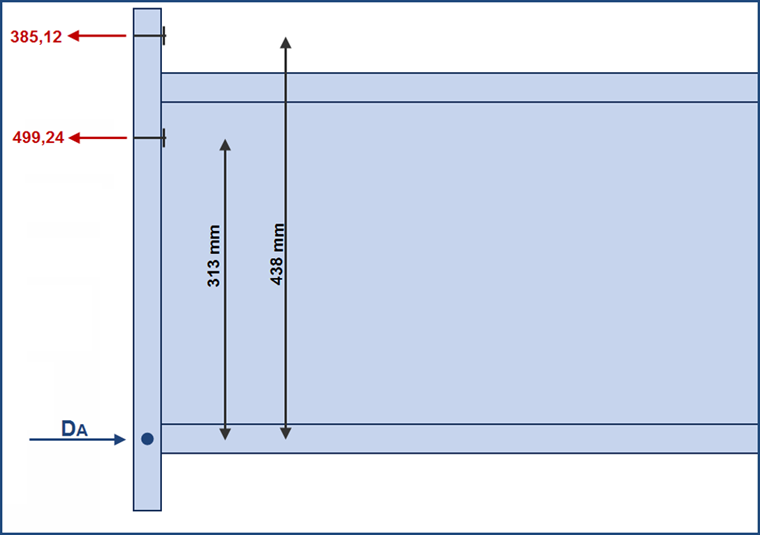
Zewnętrzny rząd śrub: 385,12 kN

Wewnętrzny rząd śrub: 499,24 kN

Nośność połączenia na zginanie

Obliczone wartości nośności obliczeniowej poszczególnych rzędów śrub należy teraz tylko pomnożyć przez odpowiednie ramię dźwigni do punktu ściskania.

Ramiona dźwigni są
438 mm dla zewnętrznego rzędu śrub,
313 mm dla wewnętrznego rzędu śrub.

Obliczeniowa nośność połączenia przy zginaniu wynosi
M_Rd = 385,12 ∙ 0,438 + 499,24 ∙ 0,313 = 324,95 kNm.

Tragfähigkeiten der Schraubenreihen und zugehörige Hebelarme

Porównanie wyników

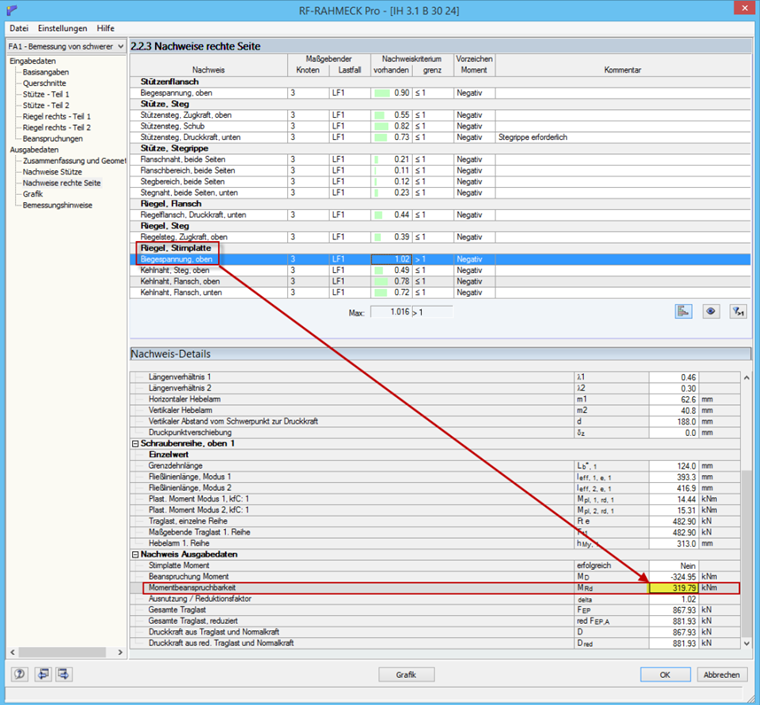
Jeżeli połączenie to jest obliczane jako połączenie sztywnej ramy w programie RF-/FRAME-JOINT Pro, wynikowa nośność obliczeniowa płyty czołowej wynosi 319,79 kNm. Zgodnie z typowymi połączeniami [2] nośność obliczeniowa wynosi 331,3 kNm, co stosunkowo dokładnie odpowiada obliczeniom ręcznym.

Stan graniczny nośności w RF-/FRAME-JOINT Pro

Autor

Pan Fröhlich zapewnia wsparcie techniczne naszym klientom i jest odpowiedzialny za rozwój w dziedzinie konstrukcji żelbetowych.

Odnośniki

Połączenia stalowe

Odniesienia

Eurocode 3: Bemessung und Konstruktion von Stahlbauten - Teil 1-8: Bemessung von Anschlüssen; EN 1993-1-8:2005 + AC:2009
K. Weynand, R. Oerder Typisierte Anschlüsse im Stahlhochbau nach DIN EN 1993-1-8. Düsseldorf: Stahlbau, 2013

Pobrane

Plik modelu w RFEM

1,16 MB

;