6094x

001576

Dipl.-Ing. (BA) Sandy Matula

2019-06-12

Упругопластический расчет сечения

В нашей статье мы опишем расчет двухпролетной балки, подвергаемой изгибу, в дополнительном модуле RF-/STEEL EC3 по норме EN 1993-1-1. Благодаря обеспечению достаточной стабилизации мы можем исключить глобальную потерю устойчивости.

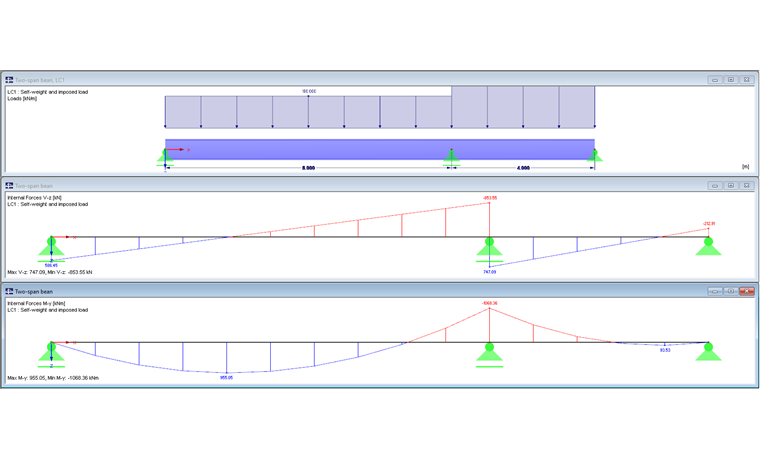
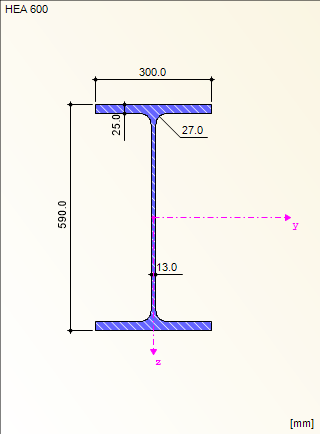
Конструктивная система и нагрузки

Конструкция, нагружение, внутренние силы

Балочный профиль HEA 600, S235

Расчет сечения

Для определения класса сечения и для расчета сечения двухпролетной балки решающей является зона внутренней опоры.

Расчет стенки балки (ψ = -1):
[1] Таблица 5.2, элементы сечения, опираемые с обеих сторон

\begin{array}{l} c = 590 - 2 \cdot (25 27) = 486 мм \\ existing \frac{c}{t_{w}} = \frac{486}{13} = 37, 38 \\ limit \frac{c}{t_{w}} = 72 \cdot ε = 72 \cdot 1 = 72 > 37, 38 \end{array}

Формула 1

Таким образом, стенка соответствует требованиям класса сечения 1.

Расчет нижней полки балки (ψ = 1):
[1] Таблица 5.2, элементы сечения, опираемые с одной стороны

\begin{array}{l} c = \frac{300 - (13 2 \cdot 27)}{2} = 116, 5 мм \\ existing \frac{c}{t_{f}} = \frac{116, 5}{25} = 4, 66 < 9 \cdot ε = 9 \cdot 1 = 9 \end{array}

Формула 2

Полки балки отвечают требованиям класса сечения 1, поэтому нужно присвоить сечению класс 1.

Упругопластический расчет сечения

\begin{array}{l} W_{pl, y} = 2 \cdot (30 \cdot 2, 5 \cdot 28, 25 27 \cdot 1, 3 \cdot 16) = 5360 {см}^{3} \\ M_{pl, y, Rd} = W_{pl, y} \cdot \frac{f_{y}}{γ_{M 0}} = 5360 \cdot \frac{23, 5}{1} = 125960 кНсм = 1259, 6 кНм \\ A_{v, z} = A - 2 \cdot b \cdot t_{f} (t_{w} 2 \cdot r) \cdot t_{f} = 226 - 2 \cdot 30 \cdot 2, 5 (1, 3 2 \cdot 2, 7) \cdot 2, 5 = 92, 75 {см}^{2} \\ V_{pl, Rd} = A_{v, z} \cdot \frac{f_{y}}{\sqrt{3} \cdot γ_{M 0}} = 92, 75 \cdot \frac{23, 5}{\sqrt{3} \cdot 1} = 1258, 41 кН \end{array}

Формула 3

Выполним расчет сечения для класса сечения 1. Балка подвергается изгибу и сдвигающему усилию над внутренней опорой и только изгибу в месте максимального момента в пролете балки. Перед расчетом несущей способности конструкции проверяется влияние взаимодействия M-V. Если V_Ed не превышает 0,5 ⋅ V_pl,Rd, нет необходимости уменьшать момент сопротивления согласно [1], раздел 6.2.8 (2).

\frac{V_{z, Ed}}{V_{pl, z, Rd}} = \frac{853, 55}{1258, 41} = 0, 678 > 0, 5

Формула 4

Требуется снижение момента сопротивления.

Для двутавровых сечений с одинаковыми полками при одноосном изгибе вокруг главной оси, уменьшение расчетного значения пластического момента сопротивления из-за нагрузки поперечной силы может быть определено следующим образом:

\begin{array}{l} ρ = {(\frac{2 \cdot V_{Ed}}{V_{pl, Rd}} - 1)}^{2} = {(\frac{2 \cdot 853, 55}{1258, 41} - 1)}^{2} = 0, 127 \\ A_{w} = h_{w} \cdot t_{w} = (59 - 2 \cdot 2, 5) \cdot 1, 3 = 70, 2 см \\ M_{pl, V, Rd} = (W_{pl, y} - \frac{ρ \cdot A_{w}^{2}}{4 \cdot t_{w}}) \cdot \frac{f_{y}}{γ_{M 0}} = (5360 - \frac{0, 127 \cdot 70, 2^{2}}{4 \cdot 1, 3}) \cdot \frac{23, 5}{1 \cdot 100} = 1231, 32 кНм \\ M_{Ed} < M_{pl, V, Rd} \to 1068, 36 < 1231, 32 кНм \end{array}

Формула 5

Автор

Г-жа Матула оказывает техническую поддержку всем нашим пользователям.

Ссылки

Программы для расчета стальных конструкций

Ссылки

Еврокод 3: Расчет стальных конструкций - Часть 1‑1: Общие правила и правила для зданий. (2010). Берлин: Beuth VerLAG GmbH
Dlubal Software, сентябрь 2017 (2020). Руководство пользователя RF-/STEEL EC3. Тифенбах: Dlubal Software, сентябрь 2017
Albert, A.: (2018). Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen (23-я издание. Кельн: Bundesanzeiger, 2016

;