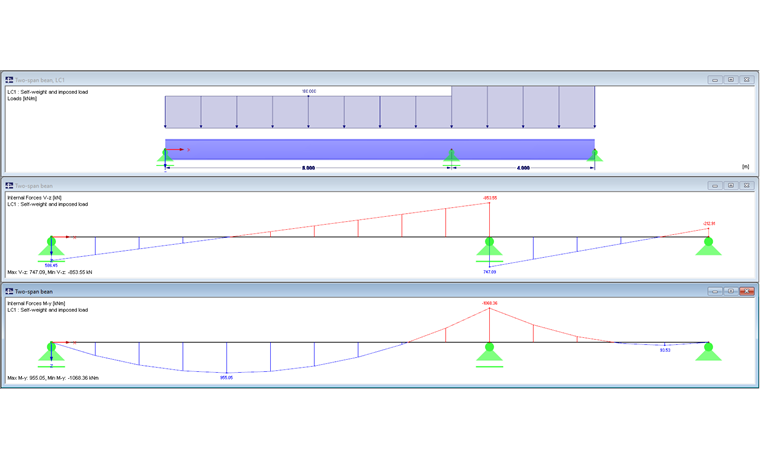
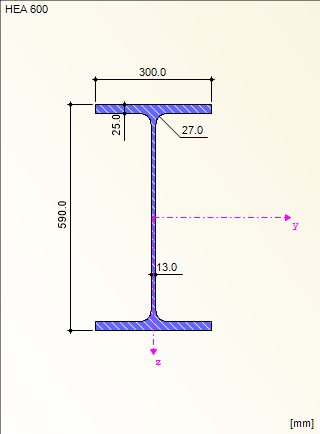
Układ konstrukcyjny i obciążenie
Wymiarowanie klasy przekroju
Rejon podpory wewnętrznej belki dwuprzęsłowej pełni nadrzędną rolę w obliczaniu klasy przekroju i przeprowadzaniu obliczeń przekroju.
Obliczenia dla środnika (ψ = -1):
[1] Tabela 5.2, części przekroju podparte po obu stronach
Tym samym przekrój spełnia wymagania dla klasy przekroju 1.
Obliczenia dla dolnego pasa (ψ = 1):
[1] Tabela 5.2, części przekroju podparte po jednej stronie
Tym samym pasy spełniają wymagania klasy przekroju 1. Przekrój należy przypisać do klasy przekroju 1.
Wymiarowanie sprężysto-plastyczne przekrojów
Obliczenia przekroju są przeprowadzane dla przekroju klasy 1. Nad wewnętrzną podporą, belka zostaje poddana zginaniu i działaniu siły tnącej, a w miejscu występowania maksymalnego momentu w przęśle, tylko zginaniu. Przed zdefiniowaniem stanu granicznego nośności konstrukcji sprawdzany jest wpływ interakcji M-V. Jeżeli VEd nie przekracza 0,5 ⋅ Vpl,Rd, nie jest wymagane zmniejszenie nośności na zginanie zgodnie z [1] Sekcji 6.2.8 (2).
Konieczna jest redukcja nośności na zginanie.
W przypadku przekrojów dwuteowych z tymi samymi kołnierzami i zginaniem dwuosiowym względem osi głównej, dopuszczalne jest zredukowanie wartości obliczeniowej plastycznej nośności na zginanie wskutek działania obciążenia siłą tnącą, jak poniżej:
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
