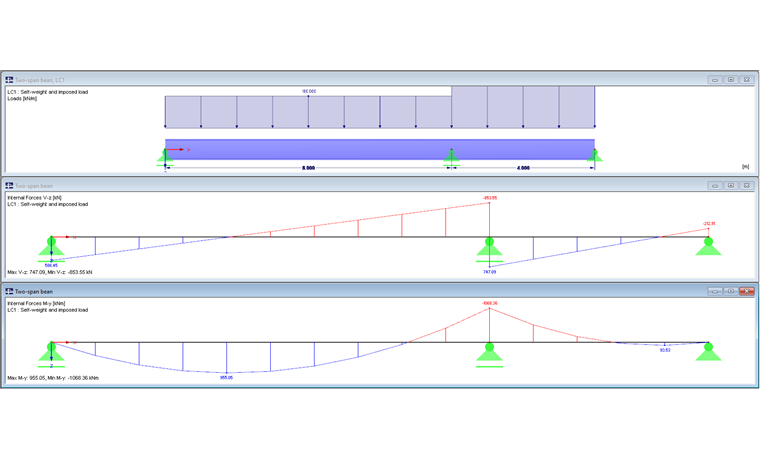
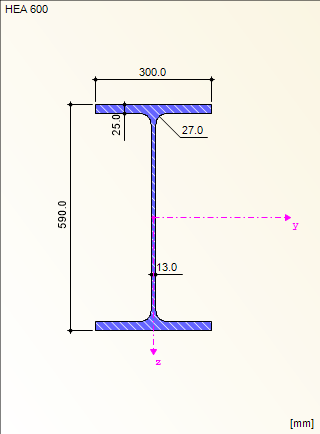
Structure et charge
Vérification de la section
L'aire de l'appui interne de la poutre à deux travées est déterminante pour la vérification de la classe de la section et celle de la section efficace.
Vérification pour l'âme (ψ = -1) :
[1] Tableau 5.2, parties de la section supportées des deux côtés.
L'âme répond donc aux exigences de la classe de section 1.
Vérification de la membrure inférieure (ψ = 1) :
[1] Tableau 5.2, parties de la section supportées d'un côté
Les membrures sont conformes aux exigences de la classe de section 1. La section doit donc être assignée à cette classe.
Vérification élasto-plastique de section
La vérification de section est effectuée pour la section de classe 1. La poutre est soumise à la flexion et à l'effort tranchant au-dessus de l'appui interne et uniquement à la flexion au niveau du moment maximal de la travée. L'influence de l'interaction MT est vérifiée avant la détermination de l'ELU de la structure. Si VEd n'est pas supérieur à 0,5 ⋅ Vpl,Rd, il n'est pas nécessaire de réduire le moment résistant selon la Section 6.2.8 (2) de [1].
Il est nécessaire de réduire le moment résistant.
Pour les sections en I avec les mêmes semelles et en flexion uniaxiale autour de l'axe principal, il est permis de déterminer la réduction de la valeur de calcul de la résistance au moment plastique due à la charge de cisaillement comme suit :
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
