6094x

001576

Dipl.-Ing. (BA) Sandy Matula

12. Juni 2019

Querschnittsnachweis elastisch-plastisch

Im Folgenden soll ein Zweifeldträger, welcher auf Biegung beansprucht ist, mit Hilfe des Zusatzmoduls RF-/STAHL EC3 nach EN 1993-1-1 nachgewiesen werden. Auf Grund ausreichender Stabilisierungsmaßnahmen wird das globale Stabilitätsversagen ausgeschlossen.

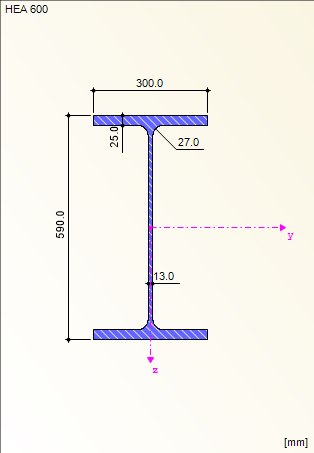
System und Belastung

System, Belastung, Schnittgrößen

Trägerprofil HEA 600, S235

Nachweis der Querschnittsklasse

Für den Nachweis der Querschnittsklasse sowie für den zu führenden Querschnittsnachweis ist der Bereich des Innenlagers des Zweifeldträgers maßgebend.

Nachweis für den Steg (ψ = -1):
[1] Tabelle 5.2, zweiseitig gestützte Querschnittsteile

\begin{array}{l} c = 590 - 2 \cdot (25 27) = 486 mm \\ vorh \frac{c}{t_{w}} = \frac{486}{13} = 37, 38 \\ grenz \frac{c}{t_{w}} = 72 \cdot ε = 72 \cdot 1 = 72 > 37, 38 \end{array}

Formel 1

Somit erfüllt der Steg die Anforderungen an die Querschnittsklasse 1.

Nachweis für den Untergurt (ψ = 1):
[1] Tabelle 5.2, einseitig gestützte Querschnittsteile

\begin{array}{l} c = \frac{300 - (13 2 \cdot 27)}{2} = 116, 5 mm \\ vorh \frac{c}{t_{f}} = \frac{116, 5}{25} = 4, 66 < 9 \cdot ε = 9 \cdot 1 = 9 \end{array}

Formel 2

Die Gurte erfüllen die Anforderungen der Querschnittsklasse 1, demnach ist der Querschnitt der Querschnittsklasse 1 zuzuordnen.

Querschnittsnachweis Elastisch-Plastisch

\begin{array}{l} W_{pl, y} = 2 \cdot (30 \cdot 2, 5 \cdot 28, 25 27 \cdot 1, 3 \cdot 16) = 5.360 {cm}^{3} \\ M_{pl, y, Rd} = W_{pl, y} \cdot \frac{f_{y}}{γ_{M 0}} = 5.360 \cdot \frac{23, 5}{1} = 125.960 kNcm = 1.259, 6 kNm \\ A_{v, z} = A - 2 \cdot b \cdot t_{f} (t_{w} 2 \cdot r) \cdot t_{f} = 226 - 2 \cdot 30 \cdot 2, 5 (1, 3 2 \cdot 2, 7) \cdot 2, 5 = 92, 75 {cm}^{2} \\ V_{pl, Rd} = A_{v, z} \cdot \frac{f_{y}}{\sqrt{3} \cdot γ_{M 0}} = 92, 75 \cdot \frac{23, 5}{\sqrt{3} \cdot 1} = 1.258, 41 kN \end{array}

Formel 3

Für den Querschnitt der Klasse 1 wird der Querschnittsnachweis geführt. Über dem Innenlager wird der Träger auf Biegung und Querkraft beansprucht, an der Stelle des maximalen Feldmomentes nur auf Biegung. Der Einfluss der M-V-Interaktion wird vor der Ermittlung der Systemtragfähigkeit geprüft. Wenn V_Ed nicht mehr als 0,5 ⋅ V_pl,Rd beträgt, muss keine Abminderung der Momententragfähigkeit nach [1] Absatz 6.2.8 (2) erfolgen.

\frac{V_{z, Ed}}{V_{pl, z, Rd}} = \frac{853, 55}{1.258, 41} = 0, 678 > 0, 5

Formel 4

Eine Abminderung der Momententragfähigkeit ist erforderlich.

Bei I-Querschnitten mit gleichen Flanschen und einachsiger Biegung um die Hauptachse darf die Abminderung des Bemessungswertes der plastischen Momententragfähigkeit infolge der Querkraftbeanspruchung wie folgt ermittelt werden:

\begin{array}{l} ρ = {(\frac{2 \cdot V_{Ed}}{V_{pl, Rd}} - 1)}^{2} = {(\frac{2 \cdot 853, 55}{1.258, 41} - 1)}^{2} = 0, 127 \\ A_{w} = h_{w} \cdot t_{w} = (59 - 2 \cdot 2, 5) \cdot 1, 3 = 70, 2 cm \\ M_{pl, V, Rd} = (W_{pl, y} - \frac{ρ \cdot A_{w}^{2}}{4 \cdot t_{w}}) \cdot \frac{f_{y}}{γ_{M 0}} = (5.360 - \frac{0, 127 \cdot 70, 2^{2}}{4 \cdot 1, 3}) \cdot \frac{23, 5}{1 \cdot 100} = 1.231, 32 kNm \\ M_{Ed} < M_{pl, V, Rd} \to 1.068, 36 < 1.231, 32 kNm \end{array}

Formel 5

Autor

Frau Matula kümmert sich im Kundensupport um die Anliegen unserer Anwender.

Links

Statik-Software für Stahlbau

Referenzen

Eurocode 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010
Handbuch RF-/STAHL EC3. Tiefenbach: Dlubal Software, Juni 2020.
Albert, A.: Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen, 23. Auflage. Köln: Bundesanzeiger, 2018

;