11343x

001622

Dipl.-Ing. (BA) Sandy Matula

2020-02-26

Расчет колонны на устойчивость под действием нормальной силы и изгиба

В этой технической статье, с помощью дополнительного модуля RF-/STEEL EC3, мы рассчитаем по норме EN 1993-1-1 шарнирную колонну, подверженную центральному действию осевой силы и действию линейной нагрузки на сильную ось.

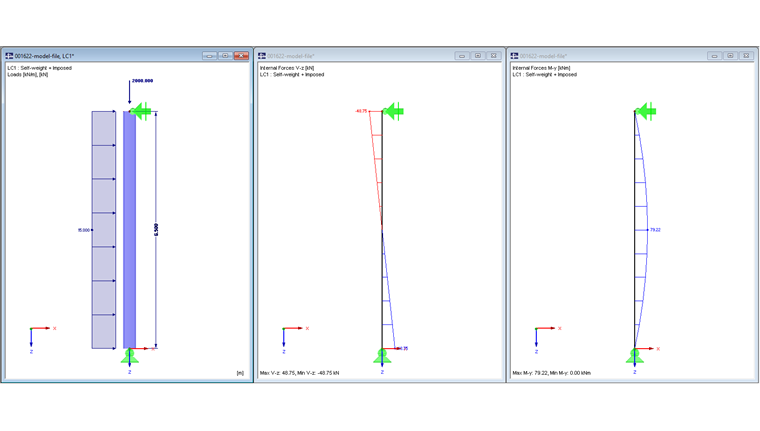
Предпосылки для расчета, нагрузки, внутренние силы и расчет сечений были описаны в одной из предыдущих статей и поэтому не будут обсуждаться повторно.

КБ | Расчет сечения колонны, подверженной действию нормальной силы и изгиба

Конструктивная система

Расчет при осевой силе и изгибающем моменте по норме EN 1993-1-1, 6.3.3 {%><#Refer [1]]]

Элементы, подвергаемые изгибу и сжатию, как правило, должны соответствовать следующим требованиям.

Расчет на потерю устойчивости при изгибе:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Расчет на потерю устойчивости при изгибе

Расчет на потерю устойчивости плоской формы изгиба:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Расчет на потерю устойчивости плоской формы изгиба

Расчет на потерю устойчивости при изгибе вокруг второстепенной оси

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Расчет на потерю устойчивости при изгибе

Расчётная длина шарнирной колонны L_cr = 6,50 м.

По норме EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, z}}}

N_{cr, z} = \frac{π^{2} \cdot E \cdot I_{z}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 10140 {cm}^{4}}{{(650 cm)}^{2}} = 4974.28 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{4974.28 kN}} = 0.924

Расчет по EN 1993-1-1, 6.3.1.2

Выбор кривой потери устойчивости при изгибе по таблице 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Выбор кривой потери устойчивости по таблице 6.2

Неустойчивость перпендикулярно оси z: Кривая напряжения при потере устойчивости BSC_z: c

В таблице 6.1 показан коэффициент несовершенства α = 0,49.

ϕ = 0.5 \cdot [1 0.49 \cdot (0.924 - 0.2) 0 . 924^{2}] = 1.104

χ_{z} = \frac{1}{1.104 \sqrt{1 . 104^{2} - 0 . 924^{2}}} = 0.585 \leq 1.0

Вычисление для расчётной проверки

У дутавров I и H и прямоугольных пустотелых профилей, которые нагружены только сжатием и изгибом, можно принять коэффициент k_zy = 0.

В результате расчет выглядит следующим образом:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} \leq 1

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

\frac{2000 kN}{\frac{0.585 \cdot 4244.1 kN}{1}} = 0.81 \leq 1

Расчет с результатом

→ Расчёт выполнен.

Расчет на потерю устойчивости плоской формы изгиба

Расчётная длина шарнирной колонны L_cr = 6,50 м.

По норме EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, y}}}

N_{cr, y} = \frac{π^{2} \cdot E \cdot I_{y}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 43190 {cm}^{4}}{{(650 cm)}^{2}} = 21187.3 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{21187.3 kN}} = 0.924

Расчет на потерю устойчивости плоской формы изгиба по к EN 1993-1-1, 6.3.1.2

Расчётная длина по таблице 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Выбор кривой потери устойчивости по таблице 6.2

Неустойчивость перпендикулярно оси y: Кривая напряжения при потере устойчивости BSC_z: b
В таблице 6.1 указан коэффициент несовершенства α = 0,34.

ϕ = 0.5 \cdot [1 0.34 \cdot (0.448 - 0.2) 0 . 448^{2}] = 0.642

χ_{y} = \frac{1}{0.642 \sqrt{0 . 642^{2} - 0 . 448^{2}}} = 0.907 \leq 1.0

вычисление потери устойчивости плоской формы изгиба

Коэффициент взаимодействия по Приложению B, таблица B1:

k_{yy} = C_{my} \cdot (1 ({\bar{λ}}_{y} - 0.2) \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}}) \leq C_{my} \cdot (1 0.8 \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}})

Коэффициент взаимодействия по Приложению B, таблица B1

Коэффициент эквивалентного момента C_my по таблице B.3:

α_{h} = \frac{M_{h}}{M_{s}} = \frac{0.00 kNm}{79.22 kNm} = 0

C_{my} = 0.95 + 0.05 \cdot α_{h} = 0.95

{\bar{λ}}_{y} = 0.448

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

k_{yy} = 0.95 \cdot (1 (0.448 - 0.2) \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.07

k_{yy, \max} = 0.95 \cdot (1 0.8 \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.34

1.07 < 1.34

Коэффициент эквивалентного момента

По норме EN 1993-1-1, 6.3.2.3:

χ_{LT} = \frac{1}{ϕ_{LT} \sqrt{ϕ_{LT}^{2} - β \cdot {\bar{λ}}_{LT}^{2}}}

ϕ_{LT} = 0.5 \cdot [1 α_{LT} \cdot ({\bar{λ}}_{LT} - {\bar{λ}}_{LT 0}) β \cdot {\bar{λ}}_{LT}^{2}]

Расчет по норме EN 1993-1-1, 6.3.2.3

По норме EN 1993-1-1, таблица 6.5:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.20 < 2

Расчет по норме EN 1993-1-1, таблица 6.5

→ кривая потери устойчивости плоской формы изгиба BC_LT : b

По норме EN 1993-1-1, таблица 6.3:

α_{LT} = 0.34

β = 0.75

λ_{LT 0} = 0.40

M_{cr} = C_{1} \cdot \frac{π^{2} \cdot E \cdot I_{z}}{{(k \cdot L)}^{2}} \cdot (\sqrt{{(\frac{k}{k_{W}})}^{2} \cdot \frac{I_{W}}{I_{z}} + \frac{{(k \cdot L)}^{2} \cdot G \cdot I_{t}}{π^{2} \cdot E \cdot I_{z}} + {(C_{2} \cdot z_{g})}^{2}} - C_{2} \cdot z_{g})

k = 1.0

k_{w} = 1.0

Расчет по норме EN 1993-1-1, таблица 6.3

C₁ и C₂ по таблице 3.2 NCCI: Упругий критический момент потери устойчивости плоской формы изгиба {%ref#Refer [5]]] (совместимые дополнительные документы к Еврокоду 3):
C₁ = 1,127
C₂ = 0,454

Расстояние от точки приложения нагрузки до центра сдвига z_g = 18 см.

M_{cr} = 1.127 \cdot \frac{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}}{{(1 \cdot 650 cm)}^{2}} \cdot (\sqrt{{(\frac{1}{1})}^{2} \cdot \frac{2883000 {cm}^{6}}{10140 {cm}^{4}} + \frac{{(1.0 \cdot 650 cm)}^{2} \cdot 8076.92 \frac{kN}{{cm}^{2}} \cdot 292.5 {cm}^{4}}{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}} + {(0.454 \cdot 18 cm)}^{2}} - 0.454 \cdot 18 cm)

M_{cr} = 115310 kNcm = 1153.10 kNm

{\bar{λ}}_{LT} = \sqrt{\frac{W_{pl, y} \cdot f_{y}}{M_{cr}}} = \sqrt{\frac{2683 {cm}^{3} \cdot 23.5 \frac{kN}{{cm}^{2}}}{115310 kNcm}} = 0.739

ϕ_{LT} = 0.5 \cdot [1 0.34 \cdot (0.739 - 0.4) 0.75 \cdot 0 . 739^{2}] = 0.762

χ_{LT} = \frac{1}{0.762 \sqrt{0 . 762^{2} - 0.75 \cdot 0 . 739^{2}}} = 0.85 < 1

Вычислить расчётную проверку

По норме EN 1993-1-1, таблица 6.7:

M_{y, Rk} = f_{y} \cdot W_{pl, y} = 23.5 \frac{kN}{{cm}^{2}} \cdot 2683 {cm}^{3} = 63050.5 kNcm = 630.51 kNm

Вычисление My,Rk

Расчёт на потерю устойчивости вокруг главной оси:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.907 \cdot 4244.10 kN}{1.0}} 1.072 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.67 \leq 1

Расчёт на потерю устойчивости вокруг главной оси

Расчёт на потерю устойчивости вокруг второстепенной оси:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.585 \cdot 4244.10 kN}{1.0}} 0.894 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.93 \leq 1

Расчёт на потерю устойчивости вокруг второстепенной оси

→ Проверки выполнены.

База знаний

KB 001622 | Расчет колонны на устойчивость под действием нормальной силы и изгиба

Автор

Г-жа Матула оказывает техническую поддержку всем нашим пользователям.

Ссылки

Программы для расчета стальных конструкций

Ссылки

Еврокод 3: Расчет стальных конструкций - Часть 1‑1: Общие правила и правила для зданий. (2010). Берлин: Beuth VerLAG GmbH
Dlubal Software, сентябрь 2017 (2020). Руководство пользователя RF-/STEEL EC3. Тифенбах: Dlubal Software, сентябрь 2017
Albert, A.: (2018). Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen (23-я издание. Кельн: Bundesanzeiger, 2016
Kuhlmann, U .; Feldmann, M .; Lindner, J .; Müller, C .; & Stroetmann, R (2014). Еврокод 3 Bemessung und Konstruktion von Stahlbauten - Диапазон 1: Общие правила и конструкция здания - DIN EN 1993-1-1 с национальным приложением, комментариями и примерами. Берлин: Beuth, 1993
бюро, А. NCCI: Elastisches kritisches Biegedrillknickmoment. Aachen: RWTH, 2010

Скачивания

Модель технической статьи | Файл RSTAB 8

352 KB

;