11343x

001622

Dipl.-Ing. (BA) Sandy Matula

2020-02-26

Stability Analysis of Column Under Axial Force and Bending

In this technical article, a hinged column with a centrally acting axial force and a line load acting on the strong axis will be designed by means of the RF-/STEEL EC3 add-on module according to EN 1993-1-1.

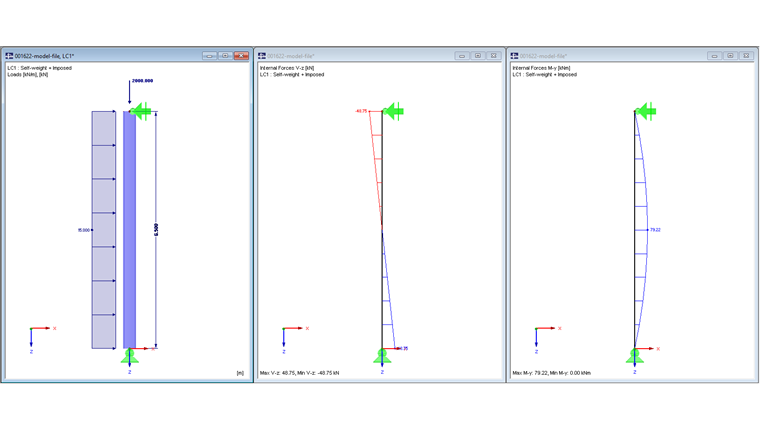
The system assumptions, loadings, internal forces, and cross-section design were explained in an earlier article and are, therefore, not discussed again.

KB | Cross-Section Design of Column Exposed to Axial Force and Bending

Structural System

Design Under Axial Force and Bending Moment According to EN 1993-1-1, 6.3.3 [1]

Components subjected to bending and compression usually have to fulfill the following requirements.

Flexural buckling design:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Flexural Buckling Design

Lateral-torsional buckling design:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Lateral-Torsional Buckling Design

Flexural Buckling Design Around Minor Axis

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Flexural Buckling Design

The effective length of the hinged column is L_cr = 6.50 m.

According to EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, z}}}

N_{cr, z} = \frac{π^{2} \cdot E \cdot I_{z}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 10140 {cm}^{4}}{{(650 cm)}^{2}} = 4974.28 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{4974.28 kN}} = 0.924

Calculation According to EN 1993-1-1, 6.3.1.2

Selection of the buckling curve according to Table 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Selection of Buckling Curve According to Table 6.2

Instability perpendicular to the z-axis: Buckling stress curve BSC_z: c

Table 6.1 shows the imperfection factor α = 0.49.

ϕ = 0.5 \cdot [1 0.49 \cdot (0.924 - 0.2) 0 . 924^{2}] = 1.104

χ_{z} = \frac{1}{1.104 \sqrt{1 . 104^{2} - 0 . 924^{2}}} = 0.585 \leq 1.0

Calculation for Design Check

For I, H, and rectangular hollow cross-sections that are only subjected to compression and bending, the coefficient k_zy = 0 may be assumed.

This results in the design as follows:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} \leq 1

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

\frac{2000 kN}{\frac{0.585 \cdot 4244.1 kN}{1}} = 0.81 \leq 1

Design with Result

→ Design is fulfilled.

Lateral-Torsional Buckling Design

The effective length of the hinged column is L_cr = 6.50 m.

According to EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, y}}}

N_{cr, y} = \frac{π^{2} \cdot E \cdot I_{y}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 43190 {cm}^{4}}{{(650 cm)}^{2}} = 21187.3 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{21187.3 kN}} = 0.924

Lateral Torsional Buckling Design According to EN 1993-1-1, 6.3.1.2

Effective length according to Table 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Selection of Buckling Curve According to Table 6.2

Instability perpendicular to the y-axis: Buckling stress curve BSC_z: b
Table 6.1 shows the imperfection factor α = 0.34.

ϕ = 0.5 \cdot [1 0.34 \cdot (0.448 - 0.2) 0 . 448^{2}] = 0.642

χ_{y} = \frac{1}{0.642 \sqrt{0 . 642^{2} - 0 . 448^{2}}} = 0.907 \leq 1.0

Calculation for Lateral-Torsional Buckling Design

Interaction factor according to Annex B, Table B1:

k_{yy} = C_{my} \cdot (1 ({\bar{λ}}_{y} - 0.2) \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}}) \leq C_{my} \cdot (1 0.8 \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}})

Interaction Factor According to Annex B, Table B1

Equivalent moment factor C_my according to Table B.3:

α_{h} = \frac{M_{h}}{M_{s}} = \frac{0.00 kNm}{79.22 kNm} = 0

C_{my} = 0.95 + 0.05 \cdot α_{h} = 0.95

{\bar{λ}}_{y} = 0.448

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

k_{yy} = 0.95 \cdot (1 (0.448 - 0.2) \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.07

k_{yy, \max} = 0.95 \cdot (1 0.8 \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.34

1.07 < 1.34

Equivalent Moment Factor

According to EN 1993-1-1, 6.3.2.3:

χ_{LT} = \frac{1}{ϕ_{LT} \sqrt{ϕ_{LT}^{2} - β \cdot {\bar{λ}}_{LT}^{2}}}

ϕ_{LT} = 0.5 \cdot [1 α_{LT} \cdot ({\bar{λ}}_{LT} - {\bar{λ}}_{LT 0}) β \cdot {\bar{λ}}_{LT}^{2}]

Calculation According to EN 1993-1-1, 6.3.2.3

According to EN 1993-1-1, Tab. 6.5:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.20 < 2

Calculation According to EN 1993-1-1, Table 6.5

→ Lateral-torsional buckling curve BC_LT: b

According to EN 1993-1-1, Tab. 6.3:

α_{LT} = 0.34

β = 0.75

λ_{LT 0} = 0.40

M_{cr} = C_{1} \cdot \frac{π^{2} \cdot E \cdot I_{z}}{{(k \cdot L)}^{2}} \cdot (\sqrt{{(\frac{k}{k_{W}})}^{2} \cdot \frac{I_{W}}{I_{z}} + \frac{{(k \cdot L)}^{2} \cdot G \cdot I_{t}}{π^{2} \cdot E \cdot I_{z}} + {(C_{2} \cdot z_{g})}^{2}} - C_{2} \cdot z_{g})

k = 1.0

k_{w} = 1.0

Design According to EN 1993-1-1, Table 6.3

C₁ and C₂ from Table 3.2 NCCI: Elastic critical torsional buckling moment [5] (compatible additional documents to Eurocode 3):
C₁ = 1.127
C₂ = 0.454

Distance from load application point to shear center z_g = 18 cm.

M_{cr} = 1.127 \cdot \frac{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}}{{(1 \cdot 650 cm)}^{2}} \cdot (\sqrt{{(\frac{1}{1})}^{2} \cdot \frac{2883000 {cm}^{6}}{10140 {cm}^{4}} + \frac{{(1.0 \cdot 650 cm)}^{2} \cdot 8076.92 \frac{kN}{{cm}^{2}} \cdot 292.5 {cm}^{4}}{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}} + {(0.454 \cdot 18 cm)}^{2}} - 0.454 \cdot 18 cm)

M_{cr} = 115310 kNcm = 1153.10 kNm

{\bar{λ}}_{LT} = \sqrt{\frac{W_{pl, y} \cdot f_{y}}{M_{cr}}} = \sqrt{\frac{2683 {cm}^{3} \cdot 23.5 \frac{kN}{{cm}^{2}}}{115310 kNcm}} = 0.739

ϕ_{LT} = 0.5 \cdot [1 0.34 \cdot (0.739 - 0.4) 0.75 \cdot 0 . 739^{2}] = 0.762

χ_{LT} = \frac{1}{0.762 \sqrt{0 . 762^{2} - 0.75 \cdot 0 . 739^{2}}} = 0.85 < 1

Design Check Calculation

According to EN 1993-1-1, Tab. 6.7:

M_{y, Rk} = f_{y} \cdot W_{pl, y} = 23.5 \frac{kN}{{cm}^{2}} \cdot 2683 {cm}^{3} = 63050.5 kNcm = 630.51 kNm

Calculation of M_y,Rk

Buckling design around the major axis:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.907 \cdot 4244.10 kN}{1.0}} 1.072 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.67 \leq 1

Buckling Design Around Major Axis

Buckling design around the minor axis:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.585 \cdot 4244.10 kN}{1.0}} 0.894 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.93 \leq 1

Buckling Design Around Minor Axis

→ Checks fulfilled.

Knowledge Base

KB 001622 | Stability Analysis of Column Under Axial Force and Bending

Author

Ms. Matula provides technical support for our customers.

Links

Structural Analysis Software for Steel Structures

References

European Committee for Standardization (CEN). (2010). Eurocode 3: Design of Steel Structures – Part 1‑1: General Rules and Rules for Buildings, EN 1993‑1‑1:2010‑12. Berlin: Beuth Verlag GmbH.
Dlubal Software. (2020). Manual RF-/STEEL EC3. Tiefenbach: Dlubal Software.
Albert, A. (2018). Schneider – Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen (23rd ed.). Cologne: Bundesanzeiger.
Kuhlmann, U.; Feldmann, M.; Lindner, J.; Müller, C.; & Stroetmann, R. (2014). Eurocode 3 - Bemessung und Konstruktion von Stahlbauten – Band 1: Allgemeine Regeln und Hochbau – DIN EN 1993-1-1 mit Nationalem Anhang, Kommentar und Beispiele Berlin: Beuth.
Bureau, A. (2010). NCCI: Elastisches kritisches Biegedrillknickmoment. Aachen: RWTH.

Downloads

Model of Technical Article | RSTAB 8 File

352 KB

;