11707x

001622

Dipl.-Ing. (BA) Sandy Matula

26. Februar 2020

Stabilitätsnachweis einer Stütze unter Normalkraft und Biegung

In diesem Fachbeitrag soll eine Pendelstütze mit einer mittig angreifenden Normalkraft und einer auf die starke Achse wirkenden Linienlast mit Hilfe des Zusatzmoduls RF-/STAHL EC3 nach EN 1993-1-1 nachgewiesen werden.

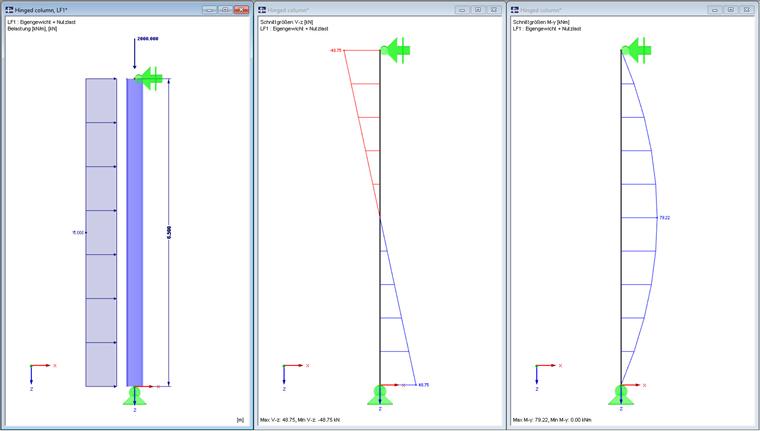
Die Systemannahmen, Belastungen, Schnittgrößen und der Querschnittsnachweis wurden bereits in einem früheren Beitrag erläutert und werden daher nicht erneut angesprochen.

KB | Querschnittsnachweis einer Stütze unter Normalkraft und Biegung

System

Nachweis unter Normalkraft und Biegemoment nach EN 1993-1-1, 6.3.3 [1]

Bauteile welche durch Biegung und Druck beansprucht werden, müssen in der Regel folgende Anforderungen erfüllen.

Nachweis gegen Biegeknicken:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Nachweis gegen Biegeknicken

Nachweis gegen Biegedrillknicken:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Nachweis gegen Biegedrillknicken

Nachweis gegen Biegeknicken um die schwache Achse

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Nachweis gegen Biegeknicken

Die Knicklänge der Pendelstütze beträgt L_cr = 6,50 m.

Nach EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, z}}}

N_{cr, z} = \frac{π^{2} \cdot E \cdot I_{z}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 10140 {cm}^{4}}{{(650 cm)}^{2}} = 4974.28 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{4974.28 kN}} = 0.924

Berechnung nach EN 1993-1-1, 6.3.1.2

Auswahl der Knicklinie nach Tabelle 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Auswahl der Knicklinie nach Tabelle 6.2

Ausweichen rechtwinklig zur z-Achse: Knickspannungslinie KSL_z: c

Aus Tabelle 6.1 ergibt sich der Imperfektionsbeiwert α = 0,49.

ϕ = 0.5 \cdot [1 0.49 \cdot (0.924 - 0.2) 0 . 924^{2}] = 1.104

χ_{z} = \frac{1}{1.104 \sqrt{1 . 104^{2} - 0 . 924^{2}}} = 0.585 \leq 1.0

Berechnung für den Nachweis

Für I-, H- und rechteckige Hohlquerschnitte, welche nur auf Druck und Biegung belastet werden, darf der Beiwert k_zy = 0 angenommen werden.

Dadurch ergibt sich der Nachweis wie folgt:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} \leq 1

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

\frac{2000 kN}{\frac{0.585 \cdot 4244.1 kN}{1}} = 0.81 \leq 1

Nachweis mit dem Ergebnis

→ Nachweis ist erfüllt.

Nachweis gegen Biegedrillknicken

Die Knicklänge der Pendelstütze beträgt auch hier L_cr = 6,50 m.

Nach EN 1993-1-1, 6.3.1.2:

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, y}}}

N_{cr, y} = \frac{π^{2} \cdot E \cdot I_{y}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 43190 {cm}^{4}}{{(650 cm)}^{2}} = 21187.3 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{21187.3 kN}} = 0.924

Nachweis gegen Biegedrillknicken nach EN 1993-1-1, 6.3.1.2

Knicklänge nach Tabelle 6.2:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Auswahl der Knicklinie nach Tabelle 6.2

Ausweichen rechtwinklig zur y-Achse: Knickspannungslinie KSL_z: b
Aus Tabelle 6.1 ergibt sich der Imperfektionsbeiwert α = 0,34.

ϕ = 0.5 \cdot [1 0.34 \cdot (0.448 - 0.2) 0 . 448^{2}] = 0.642

χ_{y} = \frac{1}{0.642 \sqrt{0 . 642^{2} - 0 . 448^{2}}} = 0.907 \leq 1.0

Berechnung für den Biegedrillknicknachweis

Interaktionsfaktor nach Anhang B, Tab. B1:

k_{yy} = C_{my} \cdot (1 ({\bar{λ}}_{y} - 0.2) \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}}) \leq C_{my} \cdot (1 0.8 \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}})

Interaktionsfaktor nach Anhang B, Tab. B1

Äquivalenter Momentenbeiwert C_my nach Tabelle B.3:

α_{h} = \frac{M_{h}}{M_{s}} = \frac{0.00 kNm}{79.22 kNm} = 0

C_{my} = 0.95 + 0.05 \cdot α_{h} = 0.95

{\bar{λ}}_{y} = 0.448

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

k_{yy} = 0.95 \cdot (1 (0.448 - 0.2) \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.07

k_{yy, \max} = 0.95 \cdot (1 0.8 \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.34

1.07 < 1.34

Äquivalenter Momentenbeiwert

Nach EN 1993-1-1, 6.3.2.3:

χ_{LT} = \frac{1}{ϕ_{LT} \sqrt{ϕ_{LT}^{2} - β \cdot {\bar{λ}}_{LT}^{2}}}

ϕ_{LT} = 0.5 \cdot [1 α_{LT} \cdot ({\bar{λ}}_{LT} - {\bar{λ}}_{LT 0}) β \cdot {\bar{λ}}_{LT}^{2}]

Berechnung nach EN 1993-1-1, 6.3.2.3

Nach EN 1993-1-1, Tab. 6.5:

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.20 < 2

Berechnung nach EN 1993-1-1, Tab. 6.5

→ Biegedrillknicklinie KL_LT: b

Nach EN 1993-1-1, Tab. 6.3:

α_{LT} = 0.34

β = 0.75

λ_{LT 0} = 0.40

M_{cr} = C_{1} \cdot \frac{π^{2} \cdot E \cdot I_{z}}{{(k \cdot L)}^{2}} \cdot (\sqrt{{(\frac{k}{k_{W}})}^{2} \cdot \frac{I_{W}}{I_{z}} + \frac{{(k \cdot L)}^{2} \cdot G \cdot I_{t}}{π^{2} \cdot E \cdot I_{z}} + {(C_{2} \cdot z_{g})}^{2}} - C_{2} \cdot z_{g})

k = 1.0

k_{w} = 1.0

Nachweis nach EN 1993-1-1, Tab. 6.3

C₁ und C₂ aus Tabelle 3.2 NCCI: Elastisches kritisches Biegedrillknickmoment [5] (kompatible Ergänzungsdokumente zu Eurocode 3):
C₁ = 1,127
C₂ = 0,454

Abstand des Lastangriffspunktes zum Schubmittelpunkt z_g = 18 cm.

M_{cr} = 1.127 \cdot \frac{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}}{{(1 \cdot 650 cm)}^{2}} \cdot (\sqrt{{(\frac{1}{1})}^{2} \cdot \frac{2883000 {cm}^{6}}{10140 {cm}^{4}} + \frac{{(1.0 \cdot 650 cm)}^{2} \cdot 8076.92 \frac{kN}{{cm}^{2}} \cdot 292.5 {cm}^{4}}{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}} + {(0.454 \cdot 18 cm)}^{2}} - 0.454 \cdot 18 cm)

M_{cr} = 115310 kNcm = 1153.10 kNm

{\bar{λ}}_{LT} = \sqrt{\frac{W_{pl, y} \cdot f_{y}}{M_{cr}}} = \sqrt{\frac{2683 {cm}^{3} \cdot 23.5 \frac{kN}{{cm}^{2}}}{115310 kNcm}} = 0.739

ϕ_{LT} = 0.5 \cdot [1 0.34 \cdot (0.739 - 0.4) 0.75 \cdot 0 . 739^{2}] = 0.762

χ_{LT} = \frac{1}{0.762 \sqrt{0 . 762^{2} - 0.75 \cdot 0 . 739^{2}}} = 0.85 < 1

Berechnung der Nachweis

Nach EN 1993-1-1, Tab. 6.7:

M_{y, Rk} = f_{y} \cdot W_{pl, y} = 23.5 \frac{kN}{{cm}^{2}} \cdot 2683 {cm}^{3} = 63050.5 kNcm = 630.51 kNm

Berechnung von M_y,Rk

Nachweis Knicken um die starke Achse:

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.907 \cdot 4244.10 kN}{1.0}} 1.072 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.67 \leq 1

Nachweis Knicken um die starke Achse

Nachweis Knicken um die schwache Achse:

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.585 \cdot 4244.10 kN}{1.0}} 0.894 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.93 \leq 1

Nachweis Knicken um die schwache Achse

→ Nachweise erfüllt.

Knowledge Base

KB 001622 | Stabilitätsnachweis einer Stütze unter Normalkraft und Biegung

Autor

Frau Matula kümmert sich im Kundensupport um die Anliegen unserer Anwender.

Links

Statik-Software für Stahlbau

Referenzen

Eurocode 3: Bemessung und Konstruktion von Stahlbauten − Teil 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau. Beuth Verlag GmbH, Berlin, 2010
Handbuch RF-/STAHL EC3. Tiefenbach: Dlubal Software, Juni 2020.
Albert, A.: Schneider - Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen, 23. Auflage. Köln: Bundesanzeiger, 2018
Kuhlmann, U.; Feldmann, M.; Lindner, J.; Müller, C.; Stroetmann, R.: Eurocode 3 Bemessung und Konstruktion von Stahlbauten - Band 1: Allgemeine Regeln und Hochbau - DIN EN 1993-1-1 mit Nationalem Anhang, Kommentar und Beispiele. Berlin: Beuth, 2014
Bureau, A.: NCCI: Elastisches kritisches Biegedrillknickmoment. Aachen: RWTH, 2010

Downloads

Modell des Fachbeitrags | RSTAB-8-Datei

352 KB

;