11343x

001622

Dipl.-Ing. (BA) Sandy Matula

26.02.2020

Analyse de stabilité d'un poteau soumis à un effort normal et à une flexion

Cet article technique est consacré à la vérification d'un poteau articulé avec un effort normal agissant au centre et une charge linéique agissant sur l'axe principal dans le module additionnel RF-/STEEL EC3 selon l'EN 1993-1-1.

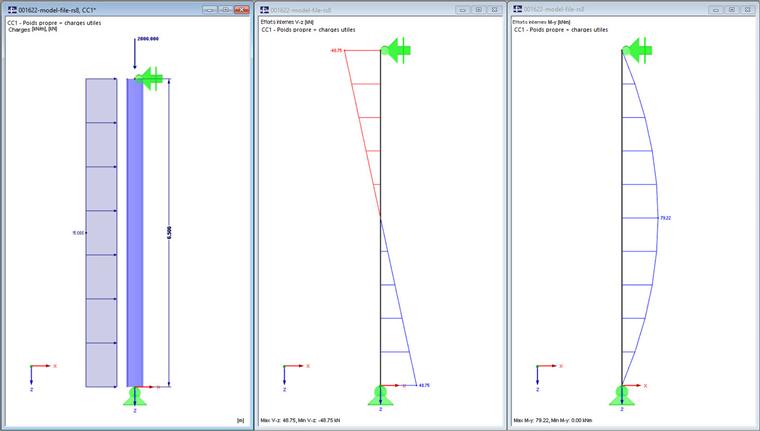
Les présupposés sur le système, les charges, les efforts internes et la vérification de la section ont déjà été expliqués dans cet article technique de notre base de connaissance et ne seront donc pas détaillés ici.

ko | Vérification de la section d'un poteau soumis à un effort normal et à une flexion

Structure

Vérification à un effort normal et un moment de flexion selon 6.3.3 de l'EN 1993-1-1 [1]

Les composants fléchis ou comprimés doivent généralement répondre aux exigences suivantes.

Vérification du flambement par flexion :

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Vérification du flambement par flexion

Vérification du déversement :

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Vérification du déversement

Vérification du flambement par flexion autour de l'axe faible

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

Vérification du flambement par flexion

La longueur de flambement du poteau articulé est ici aussi L_cr = 6,50 m.

Selon la section 6.3.1.2 de l'EN 1993-1-1 :

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, z}}}

N_{cr, z} = \frac{π^{2} \cdot E \cdot I_{z}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 10140 {cm}^{4}}{{(650 cm)}^{2}} = 4974.28 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{4974.28 kN}} = 0.924

Calcul selon EN 1993-1-1, 6.3.1.2

Choix de la courbe de flambement selon le Tableau 6.2 :

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Sélection de la courbe de flambement selon le Tableau 6.2

Flambement perpendiculaire à l'axe z : courbe de flambement BSC_z : c

Le Tableau 6.1 fournit le facteur d'imperfection α = 0,49.

ϕ = 0.5 \cdot [1 0.49 \cdot (0.924 - 0.2) 0 . 924^{2}] = 1.104

χ_{z} = \frac{1}{1.104 \sqrt{1 . 104^{2} - 0 . 924^{2}}} = 0.585 \leq 1.0

Calcul pour la vérification

Pour les sections en I, en H et rectangulaires creuses qui sont uniquement soumises à la compression et à la flexion, le facteur k_zy = 0 peut être supposé.

On obtient ainsi le calcul suivant :

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} \leq 1

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

\frac{2000 kN}{\frac{0.585 \cdot 4244.1 kN}{1}} = 0.81 \leq 1

Vérification avec le résultat

→ La vérification est effectuée.

Vérification du déversement

La longueur de flambement du poteau articulé est ici aussi L_cr = 6,50 m.

Selon la section 6.3.1.2 de l'EN 1993-1-1 :

χ = \frac{1}{ϕ \sqrt{ϕ^{2} - {\bar{λ}}^{2}}} \leq 1

ϕ = 0.5 \cdot [1 α \cdot (\bar{λ} - 0.2) {\bar{λ}}^{2}]

{\bar{λ}}_{z} = \sqrt{\frac{A \cdot f_{y}}{N_{cr, y}}}

N_{cr, y} = \frac{π^{2} \cdot E \cdot I_{y}}{l^{2}} = \frac{π^{2} \cdot 21000 kN / {cm}^{2} \cdot 43190 {cm}^{4}}{{(650 cm)}^{2}} = 21187.3 kN

{\bar{λ}}_{z} = \sqrt{\frac{180.6 {cm}^{2} \cdot 23.5 kN / {cm}^{2}}{21187.3 kN}} = 0.924

Vérification du déversement selon à l'EN 1993-1-1, 6.3.1.2

Longueur de flambement selon le Tableau 6.2 :

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.2 \leq 1.2

t_{f} = 22.5 mm \leq 100 mm

Sélection de la courbe de flambement selon le Tableau 6.2

Flambement perpendiculaire à l'axe y : courbe de flambement BSC_z : b
Le Tableau 6.1 fournit le facteur d'imperfection α = 0,34.

ϕ = 0.5 \cdot [1 0.34 \cdot (0.448 - 0.2) 0 . 448^{2}] = 0.642

χ_{y} = \frac{1}{0.642 \sqrt{0 . 642^{2} - 0 . 448^{2}}} = 0.907 \leq 1.0

Calcul pour l'analyse du déversement

Facteur d'interaction selon le Tableau B1 de l'Annexe B :

k_{yy} = C_{my} \cdot (1 ({\bar{λ}}_{y} - 0.2) \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}}) \leq C_{my} \cdot (1 0.8 \cdot \frac{N_{Ed}}{χ_{y} \cdot \frac{N_{Rk}}{γ_{M 1}}})

Facteur d'interaction selon le Tableau B1 de l'Annexe B

Facteur de moment uniforme équivalent C_my selon le tableau B.3 :

α_{h} = \frac{M_{h}}{M_{s}} = \frac{0.00 kNm}{79.22 kNm} = 0

C_{my} = 0.95 + 0.05 \cdot α_{h} = 0.95

{\bar{λ}}_{y} = 0.448

N_{Rk} = A \cdot f_{y} = 180.60 {cm}^{2} \cdot 23.5 \frac{kN}{{cm}^{2}} = 4244.1 kN

k_{yy} = 0.95 \cdot (1 (0.448 - 0.2) \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.07

k_{yy, \max} = 0.95 \cdot (1 0.8 \cdot \frac{2000 kN}{0.907 \cdot \frac{4244.10 kN}{1.0}}) = 1.34

1.07 < 1.34

Facteur de moment équivalent

Selon 6.3.2.3 de l'EN 1993-1-1 :

χ_{LT} = \frac{1}{ϕ_{LT} \sqrt{ϕ_{LT}^{2} - β \cdot {\bar{λ}}_{LT}^{2}}}

ϕ_{LT} = 0.5 \cdot [1 α_{LT} \cdot ({\bar{λ}}_{LT} - {\bar{λ}}_{LT 0}) β \cdot {\bar{λ}}_{LT}^{2}]

Calcul selon la section 6.3.2.3 de l'EN 1993-1-1

Selon le Tableau 6.5 de l'EN 1993-1-1 :

\frac{h}{b} = \frac{360 mm}{300 mm} = 1.20 < 2

Calcul selon le tableau 6.5 de l'EN 1993-1-1

→ Courbe de déversement BC_LT : b

Selon le Tableau 6.3 de l'EN 1993-1-1 :

α_{LT} = 0.34

β = 0.75

λ_{LT 0} = 0.40

M_{cr} = C_{1} \cdot \frac{π^{2} \cdot E \cdot I_{z}}{{(k \cdot L)}^{2}} \cdot (\sqrt{{(\frac{k}{k_{W}})}^{2} \cdot \frac{I_{W}}{I_{z}} + \frac{{(k \cdot L)}^{2} \cdot G \cdot I_{t}}{π^{2} \cdot E \cdot I_{z}} + {(C_{2} \cdot z_{g})}^{2}} - C_{2} \cdot z_{g})

k = 1.0

k_{w} = 1.0

Vérification selon le Tableau 6.3 de l'EN 1993-1-1

C₁ et C₂ du Tableau 3.2 NCCI : moment critique pour le déversement élastique [5] (document additionnel compatible avec l'Eurocode 3) :
C₁ = 1,127
C₂ = 0,454

Distance du point d'application de la charge au centre de cisaillement z_g = 18 cm.

M_{cr} = 1.127 \cdot \frac{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}}{{(1 \cdot 650 cm)}^{2}} \cdot (\sqrt{{(\frac{1}{1})}^{2} \cdot \frac{2883000 {cm}^{6}}{10140 {cm}^{4}} + \frac{{(1.0 \cdot 650 cm)}^{2} \cdot 8076.92 \frac{kN}{{cm}^{2}} \cdot 292.5 {cm}^{4}}{π^{2} \cdot 21000 \frac{kN}{{cm}^{2}} \cdot 10140 {cm}^{4}} + {(0.454 \cdot 18 cm)}^{2}} - 0.454 \cdot 18 cm)

M_{cr} = 115310 kNcm = 1153.10 kNm

{\bar{λ}}_{LT} = \sqrt{\frac{W_{pl, y} \cdot f_{y}}{M_{cr}}} = \sqrt{\frac{2683 {cm}^{3} \cdot 23.5 \frac{kN}{{cm}^{2}}}{115310 kNcm}} = 0.739

ϕ_{LT} = 0.5 \cdot [1 0.34 \cdot (0.739 - 0.4) 0.75 \cdot 0 . 739^{2}] = 0.762

χ_{LT} = \frac{1}{0.762 \sqrt{0 . 762^{2} - 0.75 \cdot 0 . 739^{2}}} = 0.85 < 1

Calculer la vérification

Selon le Tableau 6.7 de l'EN 1993-1-1 :

M_{y, Rk} = f_{y} \cdot W_{pl, y} = 23.5 \frac{kN}{{cm}^{2}} \cdot 2683 {cm}^{3} = 63050.5 kNcm = 630.51 kNm

Calcul de My,Rk

Vérification du flambement latéral autour de l'axe fort :

\frac{N_{Ed}}{\frac{χ_{y} \cdot N_{Rk}}{γ_{M 1}}} k_{yy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.907 \cdot 4244.10 kN}{1.0}} 1.072 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.67 \leq 1

Vérification du flambement autour de l'axe fort

Vérification du flambement latéral autour de l'axe faible :

\frac{N_{Ed}}{\frac{χ_{z} \cdot N_{Rk}}{γ_{M 1}}} k_{zy} \cdot \frac{M_{y, Ed}}{χ_{LT} \cdot \frac{M_{y, Rk}}{γ_{M 1}}} \leq 1

\frac{2000 kN}{\frac{0.585 \cdot 4244.10 kN}{1.0}} 0.894 \cdot \frac{79.22 kNm}{0.85 \cdot \frac{630.51 kNm}{1.0}} = 0.93 \leq 1

Vérification du flambement autour de l'axe faible

→ Les vérifications sont effectuées.

Base de connaissance

Ko 001622 | Analyse de stabilité d'un poteau soumis à un effort normal et à une flexion

Auteur

M. Matula fournit une assistance technique aux clients de Dlubal Software.

Liens

Logiciels de calcul de structures en acier

Références

Eurocode 3 : Eurocode 3: Calcul des structures en acier - Partie 1‑1: Règles générales et règles pour les bâtiments. (2010) Berlin : Beth Verlag GmbH
Dlubal Software. (2020). Manuel de RF-/STEEL EC3 Tiefenbach : Dlubal Software, Juni 2020.
Albert, A. (2018). Schneider – Bautabellen für Ingenieure mit Berechnungshinweisen und Beispielen (23e édition. Köln : Gazette fédérale
Kuhlmann, U.; Feldmann, M.; Lindner, J.; Müller, C.; & Stroetmann, R. (2014). Eurocode 3 Bemessung und Konstruktion von Stahlbauten - bande 1 : Règles générales et construction de bâtiments - DIN EN 1993-1-1 avec annexe nationale, commentaire et exemples. Berlin : Beth, 1993
Bureau, A. NCCI: Elastisches kritisches Biegedrillknickmoment. Aachen: RWTH, 2010

Téléchargements

Modèle de l'article technique | Fichier RSTAB 8

352 KB

;