11847x

001660

Stefan Hoffmann, M.Sc.

2020-10-14

Динамический расчет конструкций под воздействием взрывных нагрузок

В данной статье будут представлены разные сценарии взрыва, вызванного удаленной детонацией в модуле RF-DYNAM Pro - Forced Vibrations, и его эффекты, отраженные в линейном анализе изменений во времени.

1 Представления для сценария взрыва с удаленной детонацией в модуле RF-DYNAM Pro - Forced Vibrations

Основы

Конструкция должна быть спроектирована и изготовлена таким образом, чтобы она могла противостоять возможным воздействиям и влиянию, выходящему за рамки срока ее службы, а также удовлетворяла бы требованиям по пригодности к эксплуатации. В связи с этим загружения классифицируются в соответствии с их временным изменением следующим образом:

Постоянные нагрузки (например, собственный вес)
Переменные нагрузки (например, полезные нагрузки, снеговые и ветровые нагрузки)
Чрезвычайные нагрузки (например, взрыв или удар транспортного средства)

В данной статье рассмотрены чрезвычайные нагрузки от взрыва. Чрезвычайное воздействие имеет кратковременный характер и происходит с незначительной вероятностью. Однако оно может иметь серьезные последствия для устойчивости конструкции.

Взрыв - это внезапная, чрезвычайно быстро протекающая "реакция окисления или распада с резким повышением температуры и давления. Это приводит к внезапному увеличению объема газов и выделению большого количества энергии в небольшом пространстве (...). Внезапное расширение объема вызывает волну давления, которая может быть описана с помощью модели детонационной волны в случае идеального взрыва (исходящего от точечного источника)." [1] , взрыв имеет другие эффекты в виде высоких температур и выбрасываемых фрагментов (осколков, мусора). В нашей статье нагрузка на конструкцию от удаленной детонации представлена в виде чистой нагрузки от ударной волны без дальнейших воздействий взрыва.

Нагрузка от ударной волны при удаленной детонации

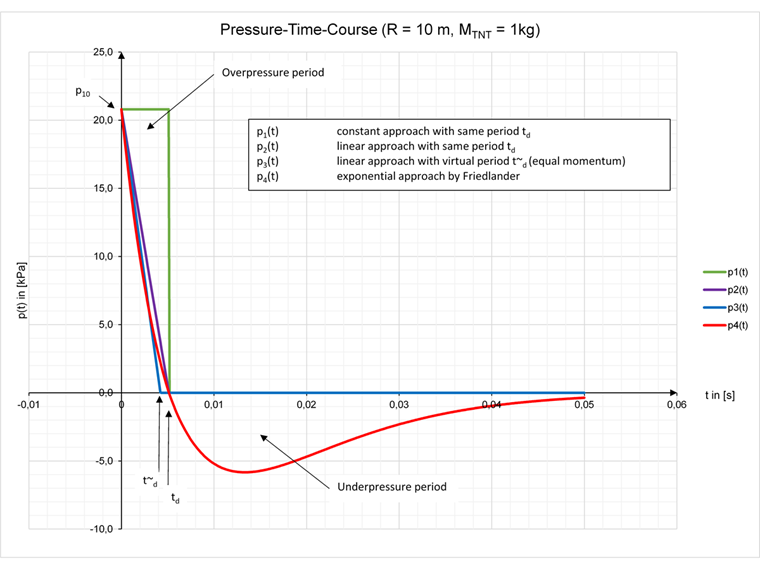
Die Luftstoßbelastung kann schematisch als Druck-Zeit-Verlauf (aus [2] dargestellt werden.

2 Динамика дистанционной детонации

Высвобожденная воздушная ударная волна с пиковым сверхвысоким давлением внезапно ударяет по конструкции. Данный процесс включает в себя фазу сверхдавления, которое действует на конструкцию в течение времени t_d, которая переходит в фазу разрежения до достижения давления окружающего воздуха. Данный экспоненциальный процесс часто упрощается до диапазона сверхдавления. При этом можно рассчитать виртуальное время t^~_d (t^~_d < t_d), в течение которого процесс приводится к линейному виду и описан с помощью импульса одинаковой величины, но полностью не принимается во внимание фаза разрежения.

Определяющими исходными значениями для расчета детонации являются расстояние до центра взрыва R и масса взрывного вещества в тротиловом эквиваленте M_TNT. Die nachfolgend genannten Formeln beziehen sich auf das in [2] entwickelte Belastungsmodell. По двум вводным значениям R и M_TNTопределяется масштабированное расстояние Z.

Z = \frac{R}{\sqrt[3]{M_{TNT}}} > 0, 5 (Дистанционный подрыв)

Z	Масштабированное расстояние [м/кг^1/3] для Z > 2,8
R	Расстояние до эпицентра взрыва [м]
M_TNT	Масса в еквиваленте ТНТ [кг]

Дистанционный взрыв, масштабированное расстояние

Далее рассчитываются значения максимального пикового сверхдавления, положительного удельного импульса и коэффициента формы. Коэффициент формы оказывает существенное влияние на протекание фазы разрежения.

{\hat{p}}_{10} = p_{0} \cdot \frac{808 \cdot [1 + {(\frac{Z}{4.5})}^{2}]}{\sqrt{1 + {(\frac{Z}{0.048})}^{2}} \cdot \sqrt{1 + {(\frac{Z}{0.32})}^{2}} \cdot \sqrt{1 + {(\frac{Z}{1.35})}^{2}}}

p₁₀	Максимальное избыточное давление на вершине от удалённого взрыва (Kinney & Graham) [кПа]
p₀	Давление окружающего воздуха в нормальных условиях (101,3 [кПа])
Z	Масштабированное расстояние [м/кг^1/3]

Максимальное избыточное давление удалённого взрыва (Kinney & Graham)

i^{+} = 2.1 \cdot \frac{R}{Z^{2}}

i⁺	Положительный, специфический импульс [кПа мс]
R	Расстояние до центра взрыва [м]
Z	Масштабированное расстояние [м/кг^1/3] для Z > 2,8

Позитивный, специфичный импульс

α = 1.5 \cdot Z^{- 0.38}

α	Множитель формы
Z	Масштабирование расстояния [м/кг^1/3] для 0,1 < Z < 30

Формула коэффициента формы

На следующем этапе мы можем выполнить расчет длительности воздействия положительного давления t_d, а также виртуальной длительности воздействия положительного давления t^~_d.

t_{d} = \frac{i^{+}}{{\hat{p}}_{10}} \cdot (\frac{α^{2}}{α - 1 + e^{- α}})

t_d	Продолжительность воздействия положительного давления
i⁺	Положительный специфический импульс [кПа мс]
p₁₀	Максимальное пиковое избыт presiónгорения на дистанции (Kinney & Graham) [кПа]
α	Коэффициент формы
e	Число Эйлера

Продолжительность положительного воздействия давления

{\tilde{t}}_{d} = \frac{2 \cdot i^{+}}{{\hat{p}}_{10}}

t^~_d	Условная продолжительность положительного воздействия давления
i⁺	Положительный удельный импульс [кПа·мс]
p₁₀	Максимальное избыточное давление на пике внешнего взрыва (Kinney и Graham) [кПа]

Виртуальная продолжительность воздействия положительного давления (тройственный подход)

Для получения кривой давление-время нужно определить значения коэффициента отражения для фазы сверхвысокого давления c_r и коэффициента отражения для фазы разрежения c^-_r. Предполагается, что поверхность отражения является бесконечной и перпендикулярной. Für Details zu den Werten wird auf [2] verwiesen.

c_{r} = \frac{8 \cdot {\hat{p}}_{10} + 14 \cdot p_{0}}{{\hat{p}}_{10} + 7 \cdot p_{0}}

c_r	Коэффициент отражения избыточного давления
p₁₀	Максимальное избыточное давление пиковых точек от дальнего взрыва(инструкция Kinney & Graham) [кПа]
p₀	Давление воздуха в окржующей среде при нормальных условиях (101,3 [кПа])

Коэффициент отражения избыточного давления

c_{r}^{-} = \frac{1.9 \cdot Z - 0.45}{Z}

c_r^-	Коэффициент отражения для разрежения
Z	Масштабированное расстояние [м/кг^1/3] для Z > 0,5

Коэффициент взвешивания для разряженного воздуха

Из всех найденных значений можно, с помощью модели загружения для полного отражения зависимости давление-время

p_{r 0} (t) = \{\begin{cases} c_{r} \cdot {\hat{p}}_{10} \cdot φ (t) & t \leq t_{d} \\ c_{r}^{-} \cdot {\hat{p}}_{10} \cdot φ (t) & t > t_{d} \end{cases}

p_r0(t)	Модель нагрузки для полного отражения зависимости давления от времени
c_r	Коэффициент отражения избыточного давления
p₁₀	Максимальное давление на фронте удалённого взрыва (Кинни и Грэхем) [кПа]
φ(t)	Функция нагрузки (постоянная/линейная/экспоненциальная функция)
t_d	Длительность воздействия положительного давления
c_r^-	Коэффициент отражения вакуума

Модель нагрузки для полного отраженного давления во времени

и выбранных функций нагрузки, отобразить загружения в RF-DYNAM Pro - Forced Vibrations в виде временных диаграмм (функций).

p_{1} (t) = \{\begin{cases} {\hat{p}}_{r 0} & t \leq t_{d} \\ 0 & t > t_{d} \end{cases}

p_{2} (t) = \{\begin{cases} {\hat{p}}_{r 0} \cdot (1 - \frac{t}{t_{d}}) & t \leq t_{d} \\ 0 & t > t_{d} \end{cases}

p_{3} (t) = \{\begin{cases} {\hat{p}}_{r 0} \cdot (1 - \frac{t}{{\tilde{t}}_{d}}) & t \leq {\tilde{t}}_{d} \\ 0 & t > {\tilde{t}}_{d} \end{cases}

p_{4} (t) = {\hat{p}}_{r 0} \cdot (1 - \frac{t}{t_{d}}) \cdot e^{- α \cdot \frac{t}{t_{d}}}

p₁(t)	Функция нагрузки иимпульс
p₂(t)	Нагрузка линейного импульса
p₃(t)	Функция нагрузки линейного импульса с виртуальным временем
p₄(t)	Экспоненциальная функция нагрузки (метод Фридлендера)
t^~_d	Виртуальная продолжительность воздействия положительного давления
t_d	Продолжительность воздействия избыточного давления
e	Число Эйлера
α	Коэффициент формы
p_r0	Полностью отражённое изменение давления во времени

Функции нагрузок

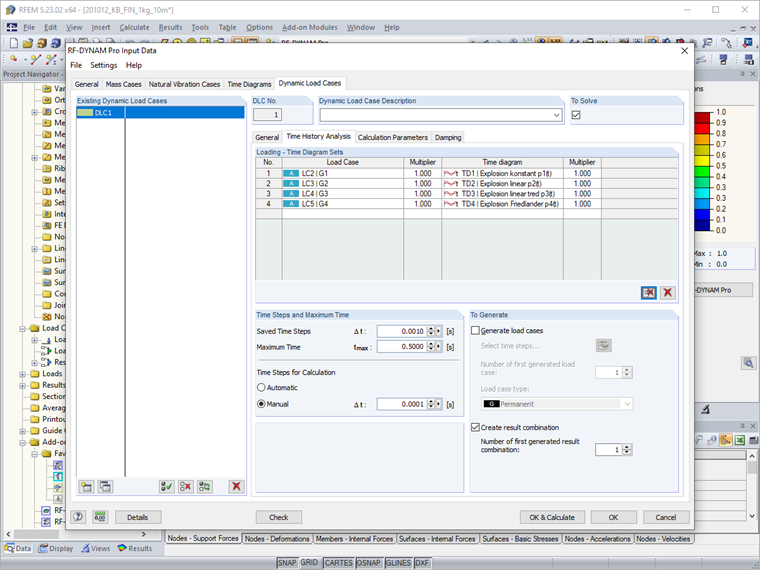
Ввод данных в RF-DYNAM Pro - Forced Vibrations

В дополнительном модуле функции нагрузки могут быть заданы в виде временных диаграмм. Временные диаграммы можно задать как переходные, периодические либо непосредственно в виде функции. Они определяют возбуждение конструкции в определенной точке. Положение нагрузки устанавливается в статических загружениях. При этом можно задать практически любой тип нагрузки. Статические загружения связаны с временными диаграммами. Это происходит в динамических загружениях. Множитель k используется для определения конечной величины возбуждающей силы.

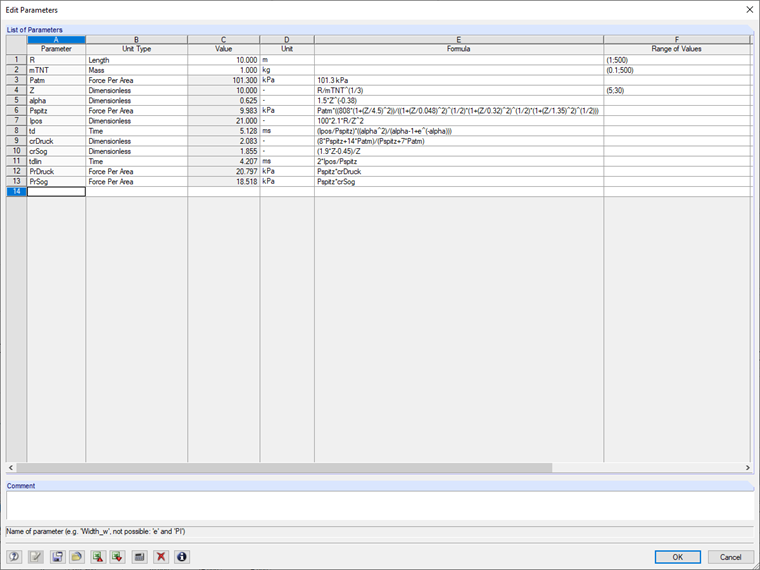
Для последующих расчетов смоделируем удаленную детонацию M_TNT = 1 кг на расстоянии R = 10 м. При использовании параметрического ввода мы получим следующие значения.

3 Перечень параметров

В перечне параметров, сохраненном в файле модели RFEM, требуется лишь откорректировать значения R и M_TNT. Insofern diese im Wertebereiche für den skalierten Abstand von 5 < Z < 30 liegen, kann das in [2] vorgestellte Berechnungsmodell verwendet werden.

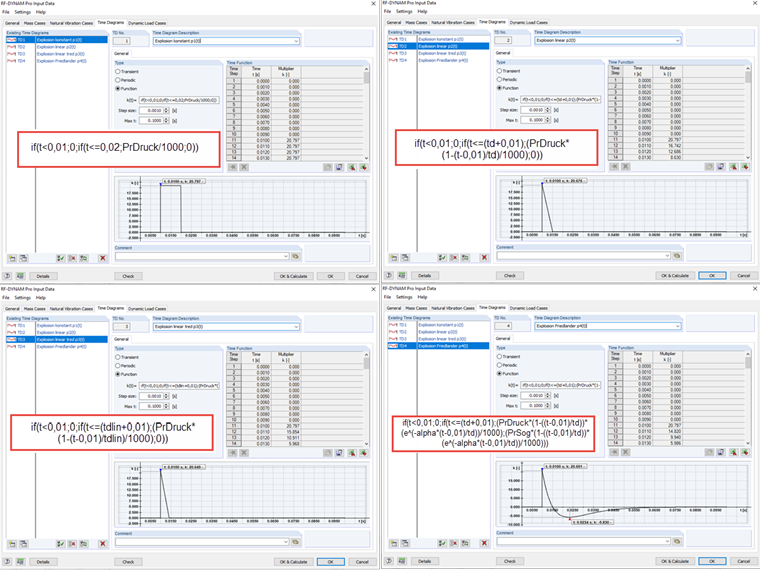
С помощью значений, рассчитанных в перечне параметров, зададим в дополнительном модуле исходные данные для четырех изображенных временных диаграмм, как показано ниже. При этом - как и во многих численных программах - давление не возникает непосредственно в момент времени t = 0 с, а в нашем примере начиная с t = 0,01 с. Для применения требуемых функций предлагается использовать вложенные функции If.

4 Обзор: ввод временных диаграмм

Чтобы сравнить четыре функции в одном файле, нужно проанализировать четыре идентичных подсистемы в динамическом загружении. Каждой подсистеме присваивается загружение, в котором на переднюю поверхность действует нагрузка 1 кН/м². Каждой подсистеме присваивается своя временная диаграмма, и, таким образом, отличная функция нагрузки.

5 Динамическое нагружение: наборы временных диаграмм

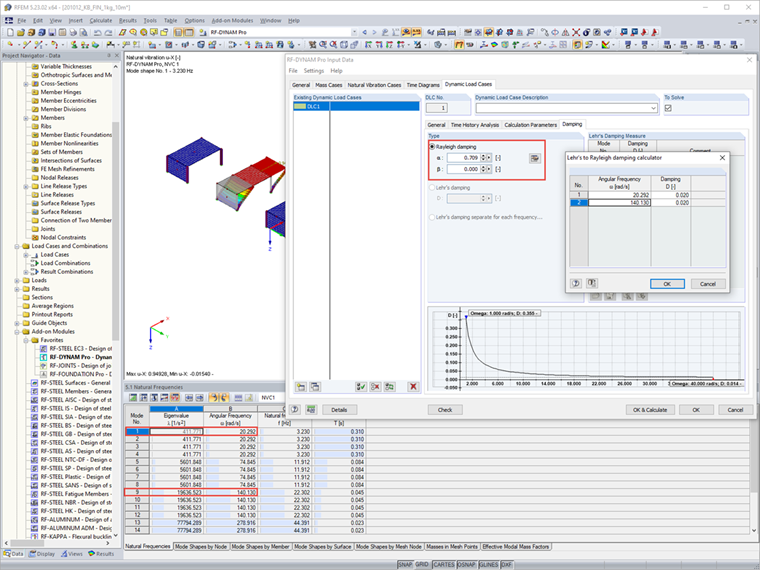
Наконец, введем для подсистем затухание Рэлея, которое можно задать по двум преобладающим собственным формам подсистем в рассматриваемом направлении.

6 Динамическое нагружение: демпфирование

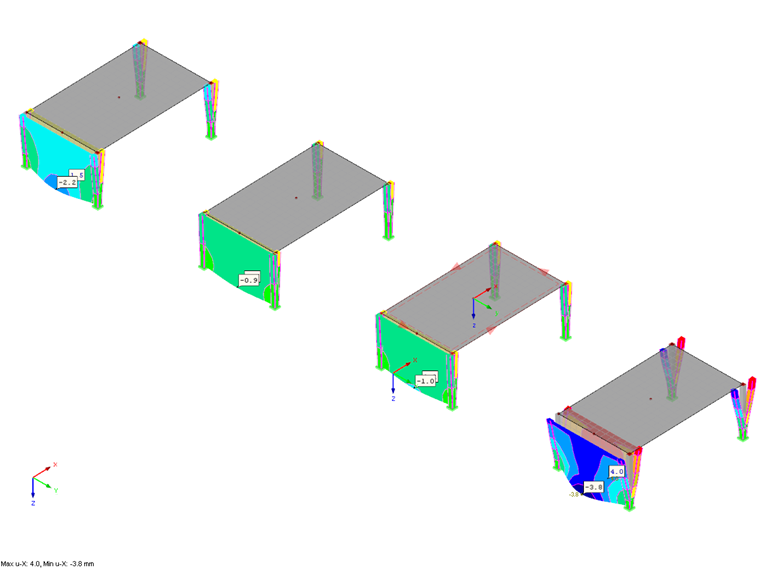
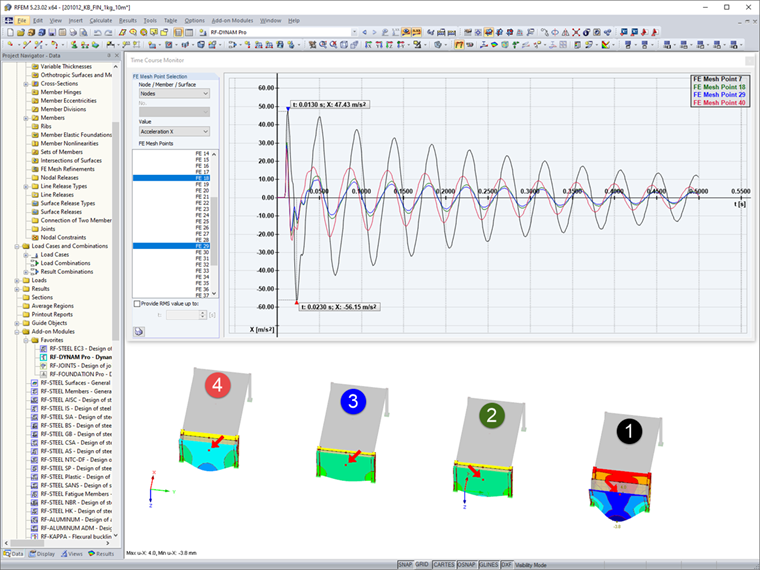
Результаты

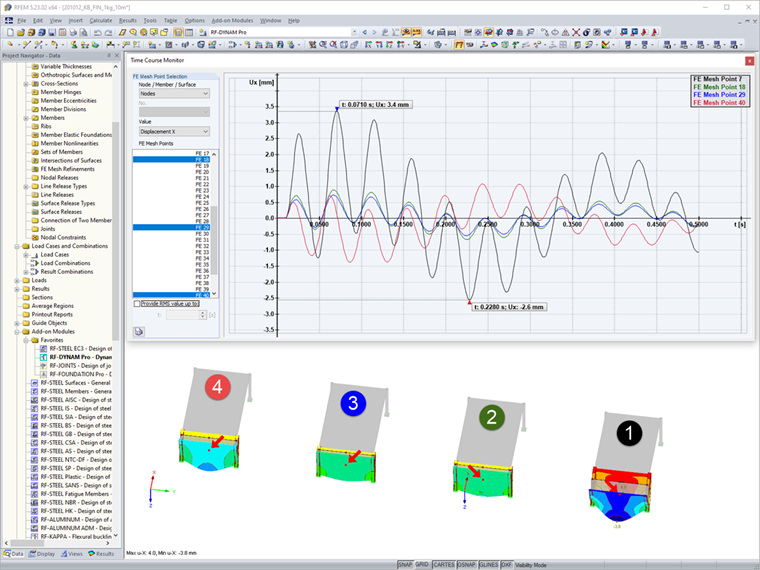
После расчета и получения результатов мы можем сравнить в данном файле четыре функции нагрузки и их влияние на подсистемы. В нашей статье мы коротко сравним только ускорение и перемещение в глобальном направлении X. Результаты можно проанализировать в интерфейсе программы в навигаторе результатов. Здесь можно отобразить различные результирующие значения для рассчитанных временных шагов. Кроме того, после анализа динамического загружения, мы получим доступ к временной диаграмме, на которой можно отобразить и сравнить дальнейшие значения в точках. В данном случае мы рассмотрим значения в центре передних поверхностей.

7 Ergebnisse Zeitverlaufsdiagramm: Beschleunigung in globaler X-Richtung

8 Ergebnisse Zeitverlaufsdiagramm: Verschiebung in globaler X-Richtung

Применение постоянного импульса p₁(t) приводит, как и ожидалось, к наибольшим значениям. Оба линеаризованных распределения p₂(t) и p₃(t) очень подобны, при этом, как и ожидалось значения p₂(t) > p₃(t). Наконец, диаграмма p₄(t) ясно показывает, что нельзя забывать о фазе разрежения, а на конструкцию влияют более высокие значения, чем при обычном линеаризованном процессе p₃(t).

Заключение

Отображение реальной кривой давление-время при удаленной детонации с помощью временных диаграмм в RF-DYNAM Pro - Forced Vibrations - это эффективный способ определения воздействия фаз сверхдавления и разрежения на конструкцию. Параметризация модели с помощью корректировки значений R и M_TNTпозволяет отобразить и сравнить различные сценарии детонации.

База знаний

КБ 001660 | Динамический расчет конструкций при взрывных нагрузках

Автор

Г-н Хоффманн оказывает техническую поддержку клиентам Dlubal Software и отвечает за координацию всех технических запросов и действий.

Ссылки

Динамический и сейсмический расчёт

Ссылки

;