11850x

001660

Stefan Hoffmann, M.Sc.

14.10.2020

Dynamická analýza konstrukcí při zatížení od výbuchu

V tomto příspěvku si ukážeme znázornění scénářů výbuchu při vzdálené detonaci v modulu RF-DYNAM Pro - Forced Vibrations a účinky porovnáme při lineární časové analýze.

1 Znázornění scénáře výbuchu při vzdálené detonaci v modulu RF-DYNAM Pro - Forced Vibrations

Základy

Konstrukci je třeba navrhnout a provést tak, aby odolávala možným zatížením a vlivům po dobu přesahující její životnost a aby také splňovala požadavky na použitelnost. V tomto ohledu se zatížení rozdělují podle proměny v čase:

Trvalá zatížení (například vlastní tíha)
Proměnná zatížení (např. užitná zatížení, zatížení sněhem a větrem)
Mimořádná zatížení (například výbuch nebo náraz vozidla)

Tématem našeho článku je mimořádné zatížení od výbuchu. Mimořádné zatížení má z časového hlediska pouze krátkou dobu trvání a vyskytuje se jen s nepatrnou pravděpodobností. Může mít ovšem závažné důsledky pro stabilitu konstrukce.

Výbuch je prudká a extrémně rychle probíhající „oxidační nebo rozkladná reakce s náhlým vzrůstem teploty a tlaku. Přitom dochází k náhlému zvětšení objemu plynů a k uvolnění velkého množství energie v malém prostoru (...). Náhlé roztažení objemu způsobí výbuch, který lze pro ideální výbuch (vycházející z jednoho bodového zdroje) popsat modelem rázové vlny.“ [1] Kromě zatížení nárazem vzduchu exploze má další účinky vlivem vysokých teplot a průmětu (střepy, úlomky). V tomto příspěvku znázorníme zatížení při vzdálené detonaci jako prosté zatížení nárazem vzduchu a další účinky výbuchu ponecháme stranou.

Zatížení nárazem vzduchu při vzdálené detonaci

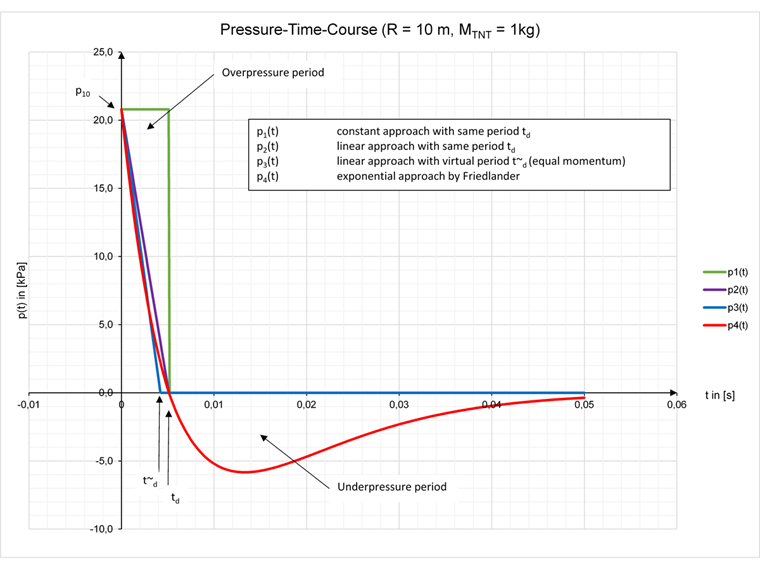
Die Luftstoßbelastung kann schematisch als Druck-Zeit-Verlauf (aus [2] dargestellt werden.

2 Časový průběh tlaku při vzdálené explozi

Uvolněná vzdušná rázová vlna s vrcholným přetlakem prudce zasáhne konstrukci. Průběh zahrnuje přetlakovou fázi, která na konstrukci působí po dobu t_da kterou následuje fáze podtlaková až po dosažení tlaku okolního vzduchu. Tento exponenciální průběh bývá často zjednodušován na oblast přetlaku. Přitom lze spočítat virtuální čas t^~_d (t^~_d < t_d), v němž se průběh linearizuje a popisuje impulzem stejné hodnoty, který ovšem zcela opomíjí fázi podtlaku.

Rozhodujícími vstupními hodnotami pro výpočet exploze jsou vzdálenost od centra výbuchu R a hmotnost M_TNT ekvivalentní nálože TNT. Die nachfolgend genannten Formeln beziehen sich auf das in [2] entwickelte Belastungsmodell. Z obou vstupních hodnot R a M_TNT se stanoví redukovaná vzdálenost Z.

Z = \frac{R}{\sqrt[3]{M_{TNT}}} > 0, 5 (Vzdálená detonace)

Z	Škálovaná vzdálenost [m/kg^1/3] pro Z > 2,8
R	Vzdálenost od středu výbuchu [m]
M_TNT	Hmotnost TNT ekvivalentu [kg]

Vzdálená exploze, Měřítkový odstup

Následně se vypočítají maximální vrcholný přetlak, kladný specifický impulz a tvarový součinitel. Tvarový součinitel má značný vliv na průběh podtlakové fáze.

{\hat{p}}_{10} = p_{0} \cdot \frac{808 \cdot [1 + {(\frac{Z}{4.5})}^{2}]}{\sqrt{1 + {(\frac{Z}{0.048})}^{2}} \cdot \sqrt{1 + {(\frac{Z}{0.32})}^{2}} \cdot \sqrt{1 + {(\frac{Z}{1.35})}^{2}}}

p₁₀	Maximální špičkový přetlak vzdálené exploze (Kinney & Graham) [kPa]
p₀	Tlak vzduchu za normálních podmínek (101,3 [kPa])
Z	Měřítkový postup [m/kg^1/3]

Maximální nadměrný tlak na špičce vzdálené exploze (Kinney & Graham)

i^{+} = 2.1 \cdot \frac{R}{Z^{2}}

i⁺	Kladný specifický impuls [kPa ms]
R	Vzdálenost od středu výbuchu [m]
Z	Měřítková vzdálenost [m/kg^1/3] pro Z > 2,8

Pozitivní, konkrétní impuls

α = 1.5 \cdot Z^{- 0.38}

α	Součinitel tvaru
Z	Měřítkový odstup [m/kg^1/3] pro 0,1 < Z < 30

Vzorec pro součinitel tvaru

V dalším kroku lze spočítat dobu trvání kladné fáze t_d a také virtuální dobu trvání kladné fáze t^~_d.

t_{d} = \frac{i^{+}}{{\hat{p}}_{10}} \cdot (\frac{α^{2}}{α - 1 + e^{- α}})

t_d	Čas trvání účinku kladného tlaku
i⁺	Klínový, specifický impuls [kPa ms]
p₁₀	Maximální špičkový nadměrný tlak vzdálené exploze (Kinney & Graham) [kPa]
α	Součinitel tvaru
e	Eulerovo číslo

Doba působení kladného tlaku

{\tilde{t}}_{d} = \frac{2 \cdot i^{+}}{{\hat{p}}_{10}}

t^~_d	Virtuální doba trvání kladného tlaku
i⁺	Klidový, specifický impuls [kPa·ms]
p₁₀	Maximální špičkový přetlak vzdálené exploze (Kinney & Graham) [kPa]

Virtuální doba trvání kladného tlaku (trojúhelníkový výpočet)

Pro stanovení průběhu odrazného tlaku v čase se stanoví součinitel odrazu pro přetlakovou fázi c_r a součinitel odrazu pro podtlakovou fázi c^-_r. Vychází se přitom z kolmé, nekonečně dlouhé odrazné plochy. Für Details zu den Werten wird auf [2] verwiesen.

c_{r} = \frac{8 \cdot {\hat{p}}_{10} + 14 \cdot p_{0}}{{\hat{p}}_{10} + 7 \cdot p_{0}}

c_r	Odrazový faktor pro přetlak
p₁₀	Maximální vrcholový přetlak dálkového výbuchu (Kinney & Graham) [kPa]
p₀	Atmosférický tlak za normálních podmínek (101,3 [kPa])

Reflexní součinitel přetlaku

c_{r}^{-} = \frac{1.9 \cdot Z - 0.45}{Z}

c_r^-	Reflexní činitel sání
Z	Škálovaná mezera [m/kg^1/3] pro Z > 0,5

Reflexní faktor pro podtlak

Ze všech stanovených hodnot pak můžeme za použití modelu zatížení pro kompletní průběh odrazného tlaku v čase

p_{r 0} (t) = \{\begin{cases} c_{r} \cdot {\hat{p}}_{10} \cdot φ (t) & t \leq t_{d} \\ c_{r}^{-} \cdot {\hat{p}}_{10} \cdot φ (t) & t > t_{d} \end{cases}

p_r0(t)	Model zatížení pro úplný průběh tlak-čas s odražením
c_r	Reflexní faktor přetlaku
p₁₀	Maximální přetlak na špičce vzdálené exploze (Kinney & Graham) [kPa]
φ(t)	Zatěžovací funkce (konstantní/ lineární/ exponentiální přístup)
t_d	Doba trvání působení kladného tlaku
c_r^-	Reflexní faktor podtlaku

Model zatížení pro úplný odrazovaný průběh závislosti tlaku na čase

a vybraných zatěžovacích funkcí znázornit zatížení v modulu RF-DYNAM Pro - Forced Vibrations jako časové diagramy (funkce).

p_{1} (t) = \{\begin{cases} {\hat{p}}_{r 0} & t \leq t_{d} \\ 0 & t > t_{d} \end{cases}

p_{2} (t) = \{\begin{cases} {\hat{p}}_{r 0} \cdot (1 - \frac{t}{t_{d}}) & t \leq t_{d} \\ 0 & t > t_{d} \end{cases}

p_{3} (t) = \{\begin{cases} {\hat{p}}_{r 0} \cdot (1 - \frac{t}{{\tilde{t}}_{d}}) & t \leq {\tilde{t}}_{d} \\ 0 & t > {\tilde{t}}_{d} \end{cases}

p_{4} (t) = {\hat{p}}_{r 0} \cdot (1 - \frac{t}{t_{d}}) \cdot e^{- α \cdot \frac{t}{t_{d}}}

p₁(t)	Zatěžovací funkce konstantního impulzu
p₂(t)	Zatěžovací funkce lineárního impulsu
p₃(t)	Funkce zatížení lineárním impulzem s virtuálním časem
p₄(t)	Exponenciální funkce zatížení (Friedlanderův přístup)
t^~_d	Virtuální doba trvání působení kladného tlaku
t_d	Trvání působení kladného tlaku
e	Eulerovo číslo
α	Součinitel tvaru
p_r0	Plně reflektovaný průběh závislosti tlaku na čase

Funkce zatížení

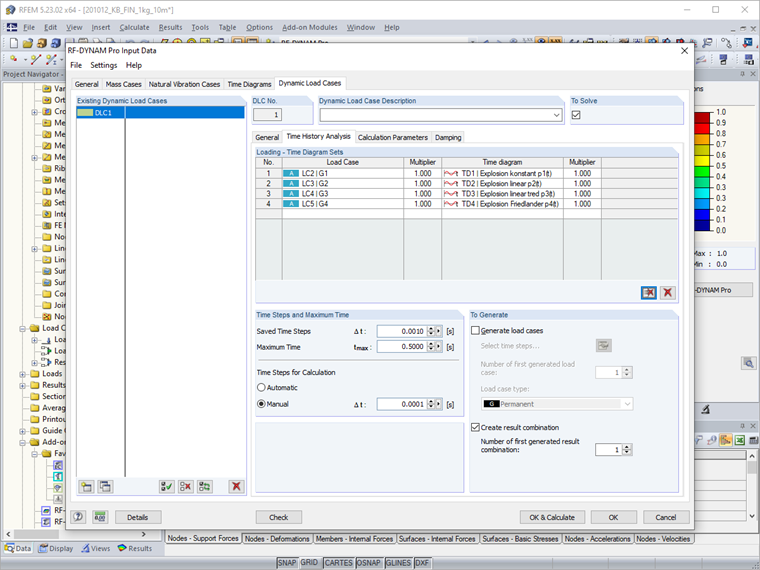
Zadání v modulu RF-DYNAM Pro - Forced Vibrations

Funkce zatížení lze v přídavném modulu zadávat jako časové diagramy. Časové diagramy lze zadat přechodné, periodické nebo přímo jako funkci. Definují buzení konstrukce v určité pozici. Poloha zatížení se stanoví ve statických zatěžovacích stavech. Lze přitom zadat téměř jakýkoli typ zatížení. Statické zatěžovací stavy jsou propojeny s časovými diagramy v dynamických zatěžovacích stavech. Násobitel k se používá pro stanovení konečné velikosti budicí síly.

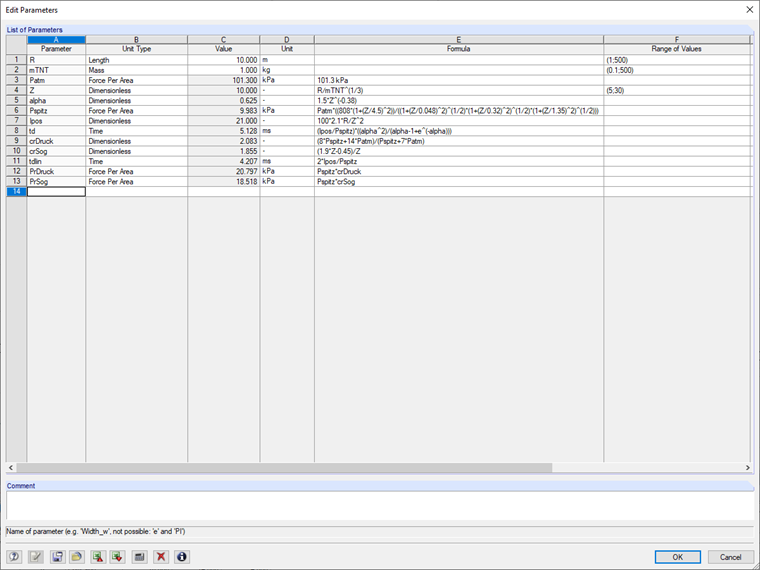
Pro následující výpočty modelujeme vzdálenou explozi M_TNT = 1 kg ve vzdálenosti R = 10 m. Při parametrickém zadání dostaneme následující hodnoty.

3 Seznam parametrů

V seznamu parametrů uloženém v souboru modelu RFEM je třeba pouze upravit hodnoty pro R a M_TNT. Insofern diese im Wertebereiche für den skalierten Abstand von 5 < Z < 30 liegen, kann das in [2] vorgestellte Berechnungsmodell verwendet werden.

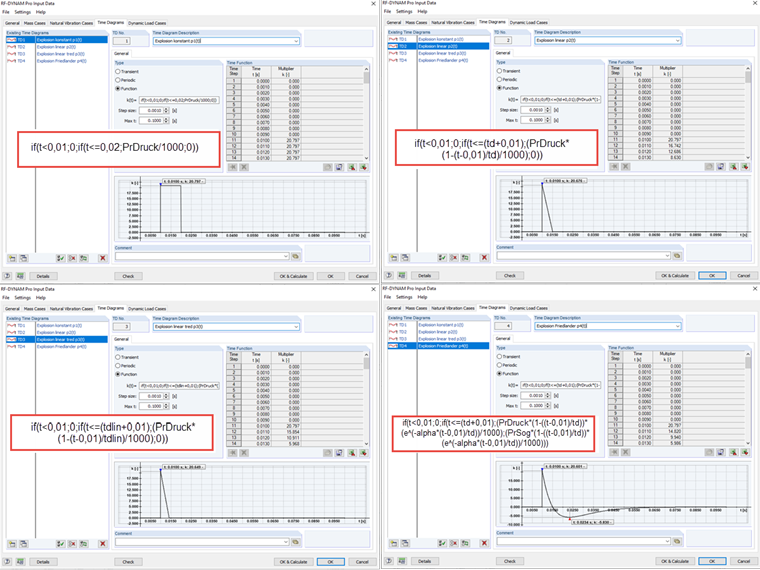
Na základě vypočítaných hodnot v seznamu parametrů zadáme v přídavném modulu vstupní údaje pro čtyři znázorněné časové diagramy. Přitom - stejně jako v mnoha numerických programech - se tlak neuvažuje okamžitě při t = 0 s, ale v našem příkladu od t = 0,01 s. Pro požadované funkce se nabízí použití vnořených funkcí If.

4 Přehled: Zadání časových diagramů

Pro porovnání těchto čtyř funkcí v jednom souboru se analyzují čtyři identické dílčí systémy v dynamickém zatěžovacím stavu. Každému dílčímu systému se přiřadí zatěžovací stav, v němž na přední plochu působí zatížení 1 kN/m². Každému dílčímu systému se přiřadí jiný časový diagram, a tedy jiná zatěžovací funkce.

5 Dynamický zatěžovací stav: Sady časových diagramů

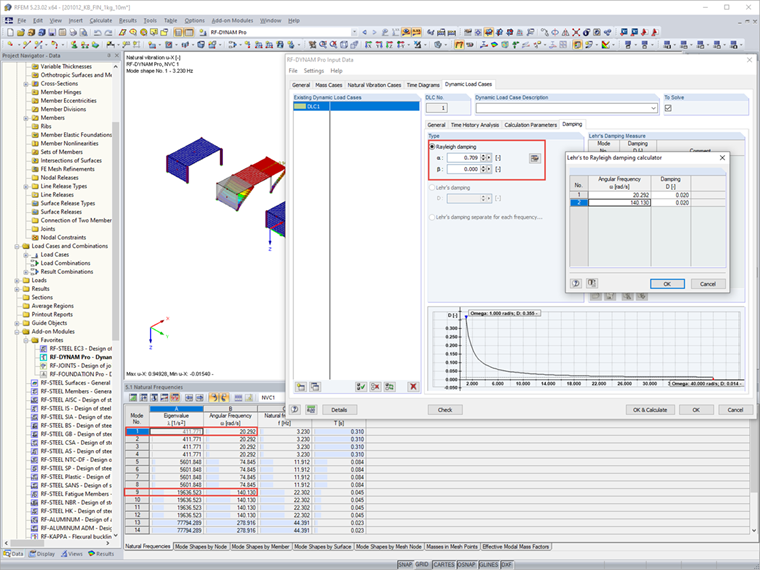
Nakonec se zadá Rayleighovo tlumení dílčích systémů, které lze určit z obou rozhodujících vlastních tvarů těchto dílčích systémů v uvažovaném směru.

6 Dynamický zatěžovací stav: Tlumení

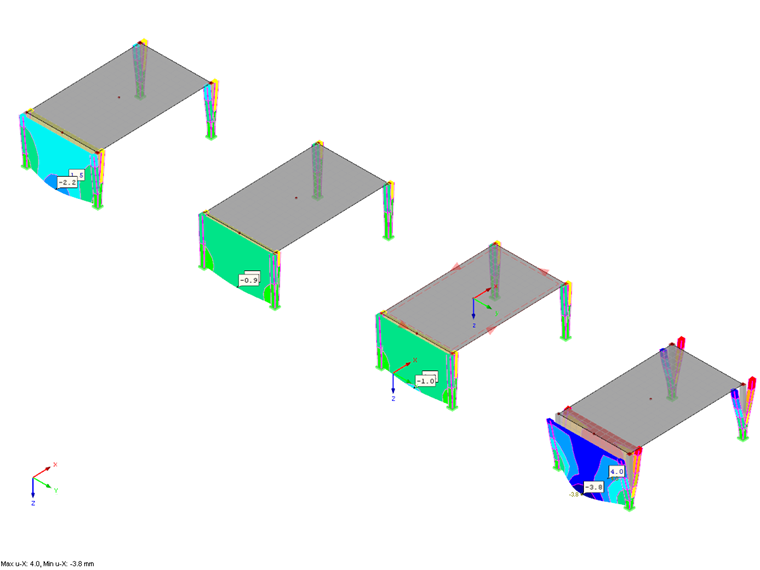
Výsledky

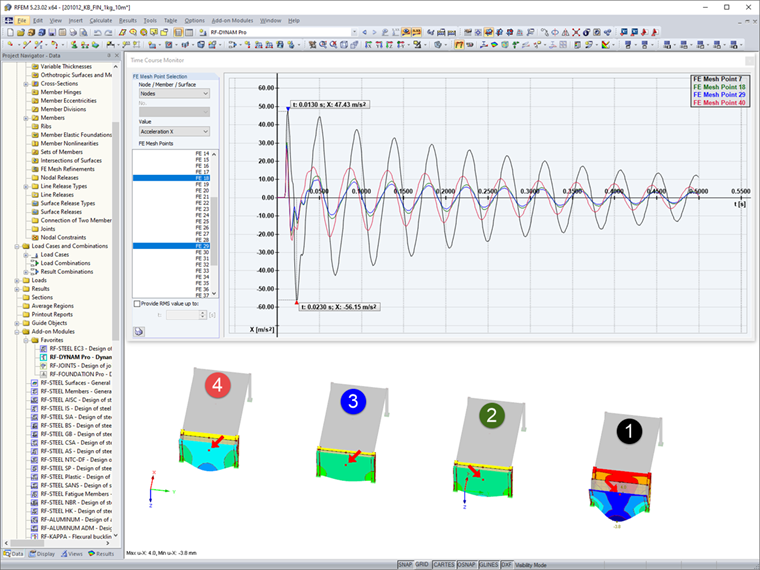
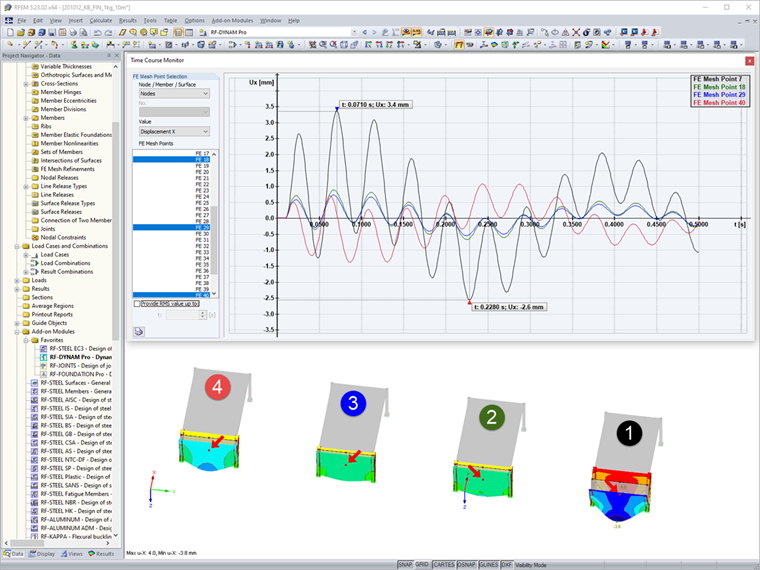
Po výpočtu a stanovení výsledků lze v daném souboru porovnat čtyři zatěžovací funkce a jejich účinky na dílčí systémy. V našem článku krátce porovnáme pouze zrychlení a posun v globálním směru X. Výsledky lze vyhodnotit v uživatelském prostředí programu v navigátoru Výsledky. Zobrazit zde lze různé výsledné hodnoty pro vypočítané časové kroky. Po analýze dynamického zatěžovacího stavu máme dále k dispozici časový diagram, v němž můžeme zobrazit další hodnoty v bodech a také je porovnat. Zde se podíváme na hodnoty uprostřed předních ploch.

7 Výsledky časového diagramu: Zrychlení v globálním směru X

8 Výsledky časového diagramu: Posun v globálním směru X

V případě konstantního impulzu p₁(t) jsou podle očekávání vykázány největší hodnoty. Oba linearizované průběhy p₂(t) a p₃(t) jsou velmi podobné, přičemž dle očekávání jsou hodnoty p₂(t) > p₃(t). Průběh p₄(t) nakonec ukazuje, že podtlakovou fázi nelze opomíjet a že ve srovnání s běžným linearizovaným průběhem p₃(t) působí na konstrukci větší hodnoty.

Závěr a výhled

Znázornění reálné křivky závislosti tlaku na čase při vzdálené explozi pomocí časových diagramů v modulu RF-DYNAM Pro - Forced Vibrations představuje účinný způsob, jak stanovit vlivy přetlakové a podtlakové fáze na konstrukci. Parametrizace modelu umožňuje při úpravě R a M_TNTzobrazit a porovnat různé scénáře výbuchu.

Databáze znalostí

KB 001660 | Dynamická analýza konstrukcí při zatížení od výbuchu

Autor

Ing. Hoffmann poskytuje technickou podporu zákazníkům společnosti Dlubal Software a je zodpovědný za koordinaci veškerých odborných dotazů a činností.

Odkazy

Dynamická a seizmická analýza

Reference

;