Введение
В предыдущей норме ACI 318-14 [2] указаны восемь уравнений для расчета прочности на сдвиг Vc - без учета пределов применения. Кроме того, пользователь может выбрать упрощенный или точный метод расчета. Целью новой концепции в норме ACI 318-19 было, кроме прочего, уменьшение количества расчетных уравнений для Vc. Концепция должна также учитывать влияние высоты элемента, коэффициента продольного армирования и осевого напряжения.
Прочность на сдвиг Vc по норме ACI 318-19
У предварительно напряженных железобетонных балок прочность на сдвиг Vc рассчитывается по норме ACI 318-19 [1] по уравнениям a) - c) из таблицы 22.5.5.1. Новые уравнения b) и c) теперь учитывают влияние высоты элемента, коэффициента продольного армирования и осевого напряжения на прочность на сдвиг Vc. Уравнение а) было по сути взято из ACI 318-14 [2].
Определение прочности на сдвиг Vc по таблице 22.5.5.1 [1] зависит от уложенной, работающей на сдвиг арматуры Av. При наличии или превышении объема минимального работающего на сдвиг армирования Av,min по п. 9.6.3.4 расчет Vc может быть выполнен по уравнению а)
или по уравнению b)
из таблицы 22.5.5.1 [1].
Если сравнить два указанных выше уравнения, то видно, что в уравнении b) коэффициент 2 λ заменен выражением 8 λ (ρw )1/3. Коэффициент продольного армирования ρw таким образом влияет на расчет прочности на сдвиг Vc. На рисунке 01 показана диаграмма 8 λ (ρw )1/3 в зависимости от ρw (при λ = 1).
,_Table_22.5.5.1,_ACI_318-19.png?mw=760&hash=df344c4cbc6e75e1a5d3e8fc97af7028acef3a2d)
При λ = 1,0 выражение 8 λ (ρw)1/3 равно значению 2 λ при коэффициенте продольного армирования ρw = 1,56 %. Для расчета Vc это означает, что при λ = 1 и коэффициенте продольного армирования ρw (более) 1,56 % по уравнению a) и при λ = 1 и ρw > 1,56% по уравнению b) мы получим более высокую прочность бетона на сдвиг. Норма позволяет применять в равной степени оба уравнения. Поэтому для экономичного расчета можно применить максимальное значение из уравнений a) и b).
Для балок с поперечным армированием Av меньше, чем Av,min, уравнение c) из таблицы 22.5.5.1 [1] должно применяться по норме ACI 318-19 [1].
За исключением переменной λs уравнение c) аналогично уравнению b), рассмотренному выше. У конструктивных элементов с малым объемом или с отсутствием работающей на сдвиг арматуры, прочность бетона на сдвиг Vc уменьшается с увеличением высоты конструктивного элемента. При вводе коэффициента λs учитывается так называемый «Size Effect». Коэффициент λs определяется по уравнению 22.5.5.1.3 [1] следующим образом.
Уменьшение прочности на сдвиг Vc,c с помощью коэффициента λs эффективно только при конструктивной высоте d (более) 10 дюймов. На рисунке 02 показана диаграмма выражения 8 λs λ (ρw)1/3 при различных значениях полезной высоты d.
,_Table_22.5.5.1_ACI_318-19.png?mw=760&hash=52b0cc2b9521511642861a07ad54c936a9837db3)
Пример: расчет требуемой работающей на сдвиг арматуры по ACI 318-19
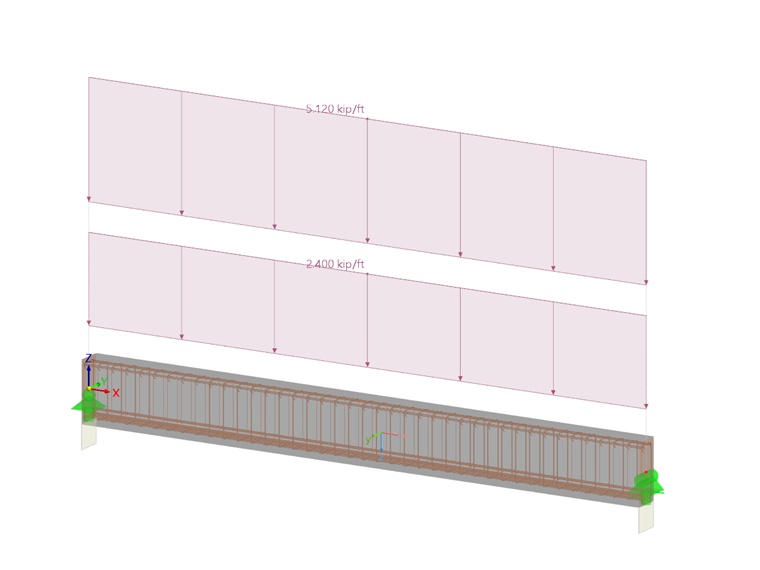
Далее мы рассчитаем по новой концепции ACI 318-19 [1] требуемую арматуру, работающую на сдвиг, для железобетонной балки, которая была рассчитана в предыдущей статье Базы знаний по ACI 318-14 [2]. На рисунке 03 показаны конструктивная модель и расчетные нагрузки.
Прямоугольное сечение имеет размеры 25 дюймов. · 11 дюймов Прочность бетона на сжатие f'c = 5000 фунт/кв.дюйм. Предел текучести арматурной стали fy = 60 000 фунт/кв.дюйм. Полезная высота растянутой арматуры равна d = 22,5 дюйма. Расчетное значение действующей поперечной силы Vu на расстоянии d от опоры составляет 61,10 тыс. фунтов.
Расчет прочности на сдвиг Vs по таблице 22.5.5.1 [1] зависит от высоты вложенной работающей на сдвиг арматуры Av. Предпосылкой для применения уравнений a) и b) является применение минимального поперечного армирования по 9.6.3.4 [1]. Поэтому на первом этапе выполняется проверка того, нужно ли учитывать минимальное армирование по 9.6.3.1 [1].
61,10 тыс. фунтов > 13,13 тыс. фунтов
Требуется минимальное поперечное армирование. Оно рассчитывается по 9.6.3.4 [1] следующим образом.
av,min = 0,12 кв. дюймов/фут
Теперь, с учетом минимальной поперечной арматуры, мы можем рассчитать прочность бетона на сдвиг Vc с помощью уравнений a) или b) по таблице 22.5.5.1 [1]. Прочность на сдвиг Vc,a рассчитывается по уравнению a) и равна Vc,a = 35,0 тыс. фунтов. Для применения уравнения b) необходимо знать значение коэффициента продольного армирования ρw . Чтобы можно было сравнить вычисленный объем арматуры, работающей на сдвиг, с результатом вычисления аддона Расчёт железобетонных конструкций, ρw определяется на основе требуемой продольной арматурой на расстоянии d от опоры. При изгибающем моменте My,u = 1533 тыс. фунтов-дюйм продольное армирование As,erf = 1,33 кв.дюйм, что дает в результате ρw = 0,536 %. На рисунке 01 показано влияние коэффициента продольного армирования ρw на расчет Vc,b. Поскольку ρw (менее) 1,5 %, по уравнению b) мы получим меньшую прочность на сдвиг Vc,b, чем по уравнение a), и мы можем пренебречь расчетом Vc,b. Тем не менее, мы выполним расчет Vc,b для наглядности.
Vc,b = 24,52 тыс. фунтов
Как и ожидалось, по уравнению b) получена более низкая прочность на сдвиг, чем по уравнению а).
Кроме того, прочность на сдвиг Vc ограничена максимальным значением Vc,max согласно 22.5.5.1.1 [1].
av,min = 0,12 кв.дюйм/фут
Теперь, с учетом минимальной поперечной арматуры, мы можем рассчитать прочность бетона на сдвиг Vc с помощью уравнений a) или b) в таблице 22.5.5.1 [1].
Прочность на сдвиг Vc,a по уравнению a) равна Vc,a = 35,0 тыс. фунтов.
Для применения уравнения b) необходимо знать значение коэффициента продольного армирования ρw. Для того, чтобы можно было сравнить вычисленный объем арматуры, работающей на сдвиг, с результатом вычисления аддона Расчёт железобетонных конструкций, ρw определяется на основе требуемой продольной арматуры на расстоянии d от опоры. При изгибающем моменте My,u = 1533 тыс.фунтов-дюйм продольное армирование As,erf = 1,33 кв.дюйм, что дает в результате ρw = 0,536 %. На рисунке 01 показано влияние коэффициента продольного армирования ρw на расчет Vc,b. Поскольку ρw (более) 1,5 %, по уравнению b) мы получим меньшую прочность на сдвиг Vc,b, чем по уравнению a), и мы можем пренебречь расчетом Vc,b. Тем не менее, мы выполним расчет Vc,b для наглядности.
Vc,b = 24,52 тыс. фунтов
Как и ожидалось, по уравнению b) получена более низкая прочность на сдвиг, чем по уравнению а).
Кроме того, прочность на сдвиг Vc ограничена максимальным значением Vc,max согласно 22.5.5.1.1 [1].
Vc,max = 87,5 тыс. фунтов
Наконец, для расчета требуемой работающей на сдвиг арматуры получена следующая применимая прочность бетона на сдвиг Vc.
Vc = max [Vc,a; Vc,b ] ≤ Vc,max
Vc = [35,0 тыс. фунтов; 24,5 тыс. фунтов] ≤ 87,5 тыс. фунтов
Vc = 35,0 тыс. фунтов
Требуемая поперечная арматура req. av рассчитывается следующим образом:
Req. av = 0,41 кв.дюйм/фут ≥ 0,12 кв.дюйм/фут
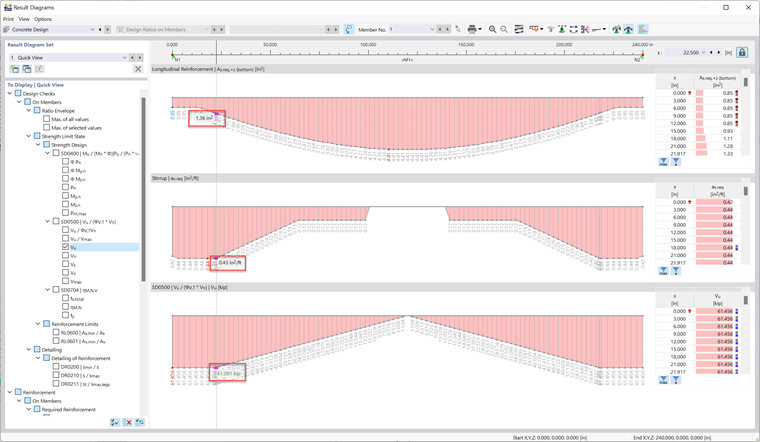
Расчет железобетонных конструкций по норме ACI 318-19 [1] можно выполнить в программе RFEM 6. В результате расчета в аддоне Расчёт железобетонных конструкций мы получим требуемую поперечную арматуру, равную 0,43 кв.дюйма/фут на расстоянии d от опоры (рисунок 04).
Примечание: Результаты, полученные в программе RFEM 6, немного отличаются от ручных расчетов из-за более точного рассчитанного значения высоты (d). RFEM 6 учитывает наличие нескольких слоев растянутой арматуры, когда как в ручных расчётах предполагается один слой.
В конце выполняется проверка максимальной несущей способности сжатого раскоса фермочной конструкции по п. 22.5.1.2.
61,10 тыс.фунтов ≤ 175,00 тыс.фунтов.
Расчет на сдвиг по норме ACI 318-19 выполнен.
Как и ожидалось, по уравнению b) получена более низкая прочность на сдвиг, чем по уравнению а).
Кроме того, прочность на сдвиг Vc ограничена максимальным значением Vc,max согласно 22.5.5.1.1 [1].
Заключение
В норме ACI 318-19 [1] представлен новый порядок определения значения прочности на сдвиг Vc. При этом удалось сократить до трех количество возможных расчетных уравнений из предыдущей версии и включить в расчет влияние нормальных напряжений, высоты элемента и коэффициента продольного армирования. Это упростило расчет прочности на сдвиг Vc.