Smyková únosnost podle ACI 318-19 v programu RFEM 6

Úvod

V předchozí normě ACI 318-14 [2] je stanoveno osm rovnic pro výpočet smykové pevnosti_Vc - bez zohlednění aplikačních mezí. Uživatel může navíc volit mezi zjednodušenou a přesnou metodou výpočtu. Cílem nové koncepce v ACI 318-19 bylo mimo jiné redukovat rovnice pro návrh V_c. Tato koncepce měla dále zohledňovat vliv výšky stavebního dílce, stupně podélného vyztužení a vliv normálového napětí.

Smyková únosnost V_c podle ACI 318-19

U nepředpjatých železobetonových nosníků se únosnost ve smyku V_c počítá podle ACI 318-19 [1] pomocí rovnic a) až c) z tabulky 22.5.5.1. With the new Equations b) and c), the member height, the longitudinal reinforcement ratio, and the normal stress now influence the shear strength, V_c. Rovnice a) byla v zásadě převzata z ACI 318-14 [2].

Stanovení smykové únosnosti V_c podle tabulky 22.5.5.1 [1] závisí na vložené smykové výztuži A_v. Pokud je k dispozici nebo je překročena minimální smyková výztuž A_v,min podle 9.6.3.4, lze V_c stanovit buď pomocí rovnice a)

nebo rovnice b)

z tabulky 22.5.5.1 [1].
Pokud porovnáme obě výše uvedené rovnice, vidíme, že v rovnici b) byl součinitel 2 λ nahrazen výrazem 8 λ (ρ_w)^1/3. Stupeň podélného vyztužení ρ_w tak ovlivňuje výpočet smykové únosnosti V_c. Image 01 shows the distribution of 8 λ (ρ_w)1/3 as a function of ρ_w (with λ = 1).

U λ = 1,0 se hodnota 8 λ (ρ_w)^1/3 rovná hodnotě 2 λ pro stupeň podélného vyztužení ρ_w = 1,56 %. Pro výpočet V_c to znamená, že pro λ = 1 a stupeň podélného vyztužení ρ_w < 1,56% vychází větší smyková únosnost betonu z rovnice a) a pro ρ_w > 1,56% z rovnice b). Norma umožňuje použití obou rovnic. Proto lze pro hospodárné posouzení použít z rovnic a) a b) maximální hodnotu.

V případě nosníků se smykovou výztuží A_v < A_v,min je třeba podle ACI 318-19 [1] uplatnit rovnici c) z tabulky 22.5.5.1 [1].

Až na proměnnou λ_s je rovnice c) shodná s výše uvedenou rovnicí b). U stavebních dílců s malou nebo žádnou smykovou výztuží se smyková únosnost V_c betonu snižuje s rostoucí výškou dílce. Zavedením součinitele λ_s se zohledňuje takzvaný „Size Effect“. Součinitel λ_s se stanoví následovně pomocí rovnice 22.5.5.1.3 [1].

Redukce smykové únosnosti V_c,c součinitelem λ_s platí teprve pro účinné výšky d > 10 in. Na obrázku 2 je znázorněn průběh výrazu 8 λ_s λ (ρ_w)^1/3 pro různé účinné výšky d.

Příklad: Výpočet požadované smykové výztuže podle ACI 318-19

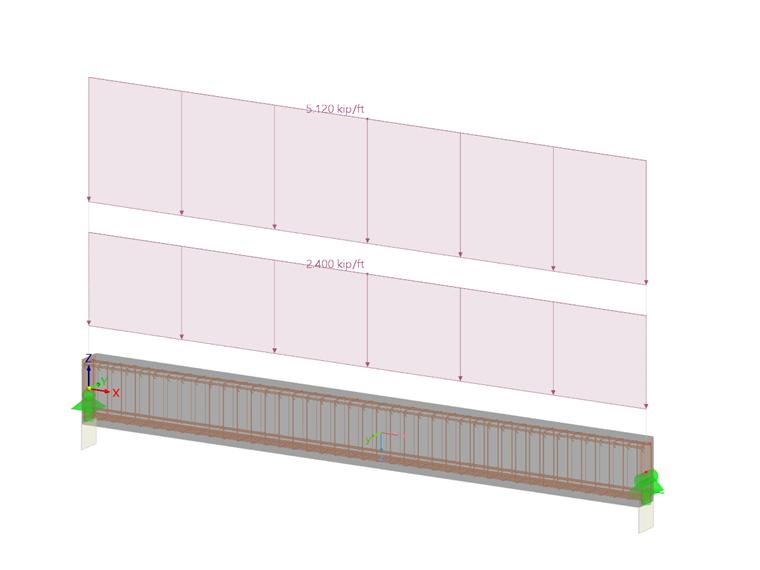
Pro železobetonový nosník, který jsme posoudili podle ACI 318-14 [2] v našem předchozím článku, níže stanovíme požadovanou smykovou výztuž podle nové koncepce ACI 318-19 [1]. Na obrázku 3 je znázorněn model konstrukce a návrhové zatížení.

Obdélníkový průřez má rozměry 25 in · 11 in. Použitý beton má pevnost v tlaku f'_c = 5 000 psi, výztužná ocel má mez kluzu f_y = 60 000 psi. Účinná výška tahové výztuže je d = 22,5 in. Návrhová hodnota působící smykové síly V_u ve vzdálenosti d od podpory činí 61,10 kips.

Stanovení smykové únosnosti V_s podle tabulky 22.5.5.1 [1] závisí na vložené smykové výztuži A_v. Předpokladem použití rovnic a) a b) je vložení minimální smykové výztuže podle 9.6.3.4 [1]. V prvním kroku se proto ověří, zda je třeba podle 9.6.3.1 [1] uvažovat minimální výztuž.

61,10 kips > 13,13 kips

Minimální smyková výztuž je tak nutná. Minimální výztuž se stanoví podle 9.6.3.4 [1] následovně.

a_v,min = 0,12 in²/ft

Při zohlednění minimální smykové výztuže lze nyní stanovit smykovou únosnost V_c betonu pomocí rovnice a) nebo b) z tabulky 22.5.5.1 [1]. Smyková únosnost V_c,a podle rovnice a) se vypočítá jako V_c,a = 35,0 kips. Pro použití rovnice b) je nutné znát stupeň podélného vyztužení ρ_w . Aby bylo možné porovnat vypočítanou smykovou výztuž s výsledkem výpočtu z addonu Posouzení železobetonových konstrukcí, stanoví se ρ_w na základě nutné podélné výztuže ve vzdálenosti d od podpory. Při ohybovém momentu M_y,u = 1533 kip-in vznikne podélná výztuž A_s,req = 1,33 in², což je ρ_w = 0,536 %. Image 01 shows the influence of the longitudinal reinforcement ratio ρw on the calculation of V_c,b. Protože je v tomto případě ρ_w < 1,5 %, dostaneme při použití rovnice b) menší únosnost ve smyku V_c,b než při použití rovnice a) a vlastně bychom mohli od výpočtu V_c,b upustit. Nicméně pro názornost výpočet V_c,b provedeme.

V_c,b = 24,52 kips

Pomocí rovnice b) se podle očekávání stanoví menší únosnost ve smyku než pomocí rovnice a).

Smyková únosnost V_c je dále podle 22.5.5.1.1 [1] omezena maximální hodnotou V_c,max.
a_v,min = 0.12 in²/ft

Při zohlednění minimální smykové výztuže lze nyní stanovit smykovou únosnost V_c betonu pomocí rovnice a) nebo b) z tabulky 22.5.5.1 [1].

Smyková únosnost V_c,a se pomocí rovnice a) stanoví jako V_c,a = 35,0 kips.

Pro použití rovnice b) je třeba znát stupeň podélného vyztužení ρ_w. Aby nakonec bylo možné vypočítanou smykovou výztuž porovnat s výsledkem výpočtu v addonu Posouzení železobetonových konstrukcí, stanoví se ρ_w na základě požadované podélné výztuže ve vzdálenosti d od podpory. A bending moment of M_y,u = 1533 kip-in results in a longitudinal reinforcement of A_s,req = 1.33 in², which is ρ_w = 0.536%. Image 01 shows the influence of the longitudinal reinforcement ratio ρ_w on the calculation of V_c,b. Since ρ_w (greater than) 1.5% here, Equation b) will result in a lower shear resistance V_c,b than Equation a) and we can skip determining V_c,b. However, we calculate V_c,b to show it.

V_c,b = 24,52 kips

Pomocí rovnice b) se podle očekávání stanoví menší únosnost ve smyku než pomocí rovnice a).

Smyková únosnost V_c je dále podle 22.5.5.1.1 [1] omezena maximální hodnotou V_c,max.

V_c,max = 87,5 kips

Nakonec se vypočítá příslušná únosnost betonu ve smyku V_c, která se uvažuje při výpočtu požadované smykové výztuže.

V_c = max [ V_c,a ; V_c,b] ≤ V_c,max

V_c = [35,0 kips ; 24,5 kips] ≤ 87,5 kips

V_c = 35,0 kips

Nutná únosnost smykové výztuže nutná a_v se vypočítá následovně:

Nutná a_v = 0.41 in²/ft ≥ 0.12 in²/ft

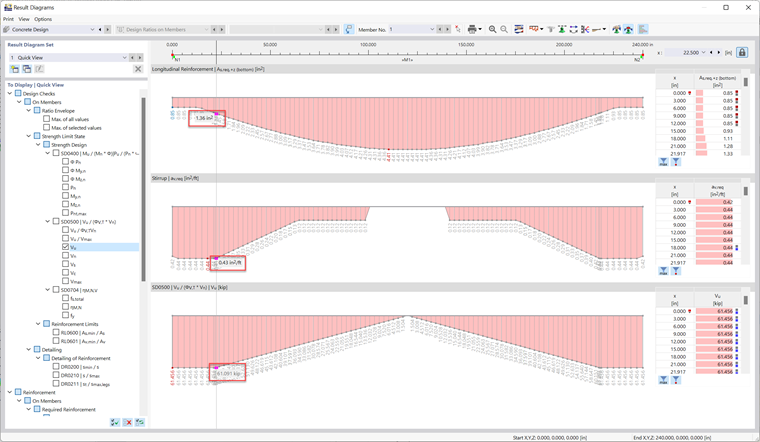
V programu RFEM 6 lze provést posouzení železobetonu podle ACI 318-19 [1]. The Concrete Design Add-on also calculates a required shear reinforcement of 0.43 in²/ft at the distance d from the support (see Image 04).

Pozor: Výsledky v programu RFEM 6 se mírně liší od ručních výpočtů z důvodu přesnější hodnoty pro vypočítanou výšku (d). RFEM 6 zohledňuje, že existuje více vrstev tahové výztuže, zatímco ruční výpočty uvažují jednu vrstvu.

Nakonec se ještě ověří maximální únosnost tlakové diagonály příhradové konstrukce podle článku 22.5.1.2.

61,10 kips ≤ 175,00 kips.

Posouzení na smyk podle ACI 318-19 je tak splněno.
Pomocí rovnice b) se podle očekávání stanoví menší únosnost ve smyku než pomocí rovnice a).

Smyková únosnost V_c je dále podle 22.5.5.1.1 [1] omezena maximální hodnotou V_c,max.

Závěr

Normou ACI 318-19 [1] byla zavedena nová koncepce stanovení únosnosti ve smyku V_c. Podařilo se přitom omezit počet možných návrhových rovnic z předešlých verzí na tři rovnice a vzít přitom v potaz vliv normálového napětí, výšky stavebního dílce a stupně podélného vyztužení. Tím se výpočet únosnosti ve smyku V_c zjednodušuje.