Einführung
In der Vorgängernorm ACI 318-14 [2] werden für die Berechnung der Schubfestigkeit Vc – ohne Berücksichtigung der Anwendungsgrenzen – acht Gleichungen angegeben. Dabei kann der Anwender noch zwischen einem vereinfachten und einem genauen Berechnungsverfahren wählen. Eine Zielsetzung für das neue Konzept im ACI 318-19 war unter anderem auch die Reduzierung der Bemessungsgleichungen für Vc. Weiter sollte das Konzept den Einfluss der Bauteilhöhe, des Längsbewehrungsgrad und der Normalspannung berücksichtigen.
Schubwiderstand Vc nach ACI 318-19
Für nicht vorgespannte Stahlbetonbalken erfolgt die Berechnung des Schubwiderstandes Vc nach ACI 318-19 [1] mit den Gleichungen a) bis c) aus Tabelle 22.5.5.1. Mit den neuen Gleichungen b) und c) wird der Einfluss von Bauteilhöhe, Längsbewehrungsgrad sowie Normalspannung auf die Schubfestigkeit Vc berücksichtigt. Gleichung a) wurde im Wesentlichen ACI 318-14 [2] entnommen.
Die Ermittlung des Schubwiderstandes Vc nach Tabelle 22.5.5.1 [1] ist abhängig von der eingelegten Schubbewehrung Av. Ist die Mindestschubbewehrung Av,min nach 9.6.3.4 vorhanden beziehungsweise überschritten, darf die Berechnung von Vc entweder nach Gleichung a)
oder Gleichung b)
aus Tabelle 22.5.5.1 [1] durchgeführt werden.
Vergleicht man die beiden oben gezeigten Gleichungen, dann erkennt man, dass in Gleichung b) der Faktor 2 λ mit dem Term 8 λ (ρw)1/3 ersetzt wurde. Dadurch nimmt der Längsbewehrungsgrad ρw Einfluss auf die Berechnung des Schubwiderstandes Vc. Image 01 shows the distribution of 8 λ (ρw)1/3 as a function of ρw (with λ = 1).
Für λ = 1,0 wird 8 λ (ρw)1/3 bei einem Längsbewehrungsgrad ρw = 1,56 % gleich dem Wert 2 λ. Bei der Berechnung von Vc ergibt sich aus Gleichung a) für λ= 1 und einem Längsbewehrungsgrad ρw (größer) 1,56% und Gleichung b) für λ= 1 und ρw > 1,56% der größere Betonschubwiderstand. Die Norm erlaubt die Anwendung beider Gleichungen. Für eine kostengünstige Bemessung kann daher der Maximalwert aus den Gleichungen a) und b) verwendet werden.
Für Träger mit Schubbewehrung Av kleiner Av,min ist gemäß ACI 318-19 Gleichung c) der Tabelle 22.5.5.1 [1] zu verwenden.
Die Formel c) gleicht bis auf die Variable λs der oben diskutierten Gleichung b). Bei Bauteilen ohne oder mit geringer Schubbewehrung nimmt der Betonschubwiderstand Vc mit zunehmender Bauteilhöhe ab. Mit Einführung des Faktors λs wird der sogenannte "Size Effect" berücksichtigt. Der Faktor λs wird nach Gleichung 22.5.5.1.3 [1] wie folgt ermittelt.
Die Abminderung des Schubwiderstands Vc,c durch den Faktor λs ist nur für statische Höhen d (größer) 10in wirksam. Bild 02 zeigt den Verlauf des Terms 8 λs λ (ρw)1/3 für unterschiedliche statische Nutzhöhen d.
Beispiel: Berechnung der erforderlichen Schubbewehrung nach ACI 318-19
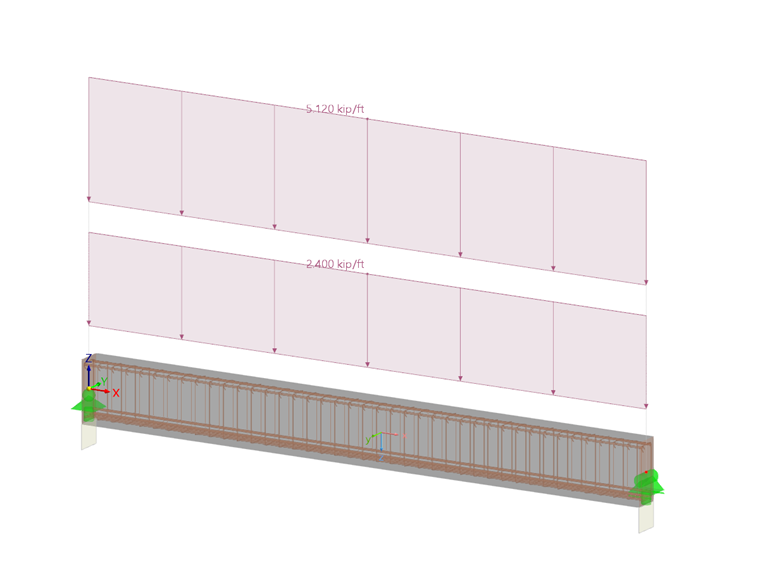
Nachfolgend wird für einen Stahlbetonbalken, welcher in einem früheren Fachbetrag gemäß ACI 318-14 [2] bemessen wurde, die erforderliche Schubbewehrung nach dem neuen Konzept des ACI 318-19 [1] ermittelt. Bild 03 zeigt nochmals das statische System und die Bemessungslast.
Der Rechteckquerschnitt hat die Abmessungen 25in · 11in. Der Beton hat eine Druckfestigkeit von f'c = 5.000 psi. Die Streckgrenze des verwendeten Betonstahls beträgt fy = 60.000 psi. Die statische Nutzhöhe der Zugbewehrung wird mit d = 22,5 in angesetzt. Der Bemessungswert der wirkenden Querkraft Vu im Abstand d vom Auflager beträgt 61,10 kips.
Die Ermittlung des Schubwiderstandes Vs nach Tabelle 22.5.5.1 [1] ist abhängig von der Höhe der eingelegten Schubbewehrung Av. Voraussetzung für die Anwendung der Gleichungen a) und b) ist, dass die Mindestschubbewehrung nach 9.6.3.4 [1] verwendet wird. Aus diesem Grund wird im ersten Schritt geprüft, ob nach 9.6.3.1 [1] eine Mindestbewehrung zu berücksichtigen ist.
61,10 kips > 13,13 kips
Dadurch ist eine Mindestschubbewehrung erforderlich. Diese berechnet sich nach 9.6.3.4 [1] wie folgt.
av,min = 0,12 in²/ft
Unter Berücksichtigung der Mindestschubbewehrung kann der Betonschubwiderstand Vc nun mit den Gleichungen a) oder b) der Tabelle 22.5.5.1 [1] ermittelt werden. Der Schubwiderstand Vc,a nach Gleichung a) berechnet sich zu Vc,a = 35,0 kips. Für die Anwendung der Gleichung b) ist die Kenntnis des Längsbewehrungsgrads ρw notwendig. Damit die berechnete Schubbewehrung mit dem Berechnungsergebnis des Add-Ons Betonbemessung verglichen werden kann, wird ρw mit der erforderlichen Längsbewehrung im Abstand d vom Auflager bestimmt. Bei einem Biegemoment von My,u = 1533 kip-in ergibt sich eine Längsbewehrung von As,erf = 1,33 in², was ρw = 0,536% ergibt. Image 01 shows the influence of the longitudinal reinforcement ratio ρw on the calculation of Vc,b. Da hier ρw (kleiner) 1,5% ist, führt Gleichung b) zu einem geringeren Schubwiderstand Vc,b als Gleichung a) und die Ermittlung von Vc,b kann übersprungen werden. Zur Veranschaulichung wird die Berechnung von Vc,b dennoch durchgeführt.
Vc,b = 24,52 kips
Wie erwartet liefert Gleichung b) einen geringeren Schubwiderstand als Gleichung a).
Zusätzlich ist der Schubwiderstand Vc auf den Maximalwert Vc,max nach 22.5.5.1.1 [1] begrenzt.
av,min = 0.12 in²/ft
Unter Berücksichtigung der Mindestschubbewehrung kann der Betonschubwiderstand Vc nun mit den Gleichungen a) oder b) der Tabelle 22.5.5.1 [1] ermittelt werden.
Der Schubwiderstand Vc,a nach Gleichung a) berechnet sich zu Vc,a = 35,0 kips
Für die Anwendung der Gleichung b) ist die Kenntnis des Längsbewehrungsgrads ρw notwendig. Um die berechnete Schubbewehrung mit dem Berechnungsergebnis des Add-Ons Betonbemessung vergleichen zu können, wird ρw mit der erforderlichen Längsbewehrung im Abstand d vom Auflager ermittelt. Bei einem Biegemoment von My,u = 1533 kip-in ergibt sich eine Längsbewehrung von As,erf = 1,33 in², was ein ρw = 0,536 % ergibt. In Bild 01 wird der Einfluss des Längsbewehrungsgrades ρw auf die Berechnung von Vc,b gezeigt. Da hier ρw < 1,5 % ist, wird Gleichung b) einen geringeren Schubwiderstand Vc,b als Gleichung a) ergeben und es könnte eigentlich auf die Ermittlung von Vc,b verzichtet werden. Zur Veranschaulichung wird die Berechnung von Vc,b dennoch durchgeführt.
Vc,b = 24,52 kips
Wie erwartet liefert Gleichung b) einen geringeren Schubwiderstand als Gleichung a).
Zusätzlich ist der Schubwiderstand Vc auf den Maximalwert Vc,max nach 22.5.5.1.1 [1] begrenzt.
Vc,max = 87,5 kips
Abschließend ergibt sich für die Berechnung der erforderlichen Schubbewehrung folgender ansetzbarer Schubkraftwiderstand Vc des Betons.
Vc = max [ Vc,a ; Vc,b] ≤ Vc,max
Vc = [35,0 kips ; 24,5 kips] ≤ 87,5 kips
Vc = 35,0 kips
Die erforderliche Schubbewehrung erf. av berechnet sich wie folgt:
Erf. av = 0.41 in²/ft ≥ 0.12 in2/ft
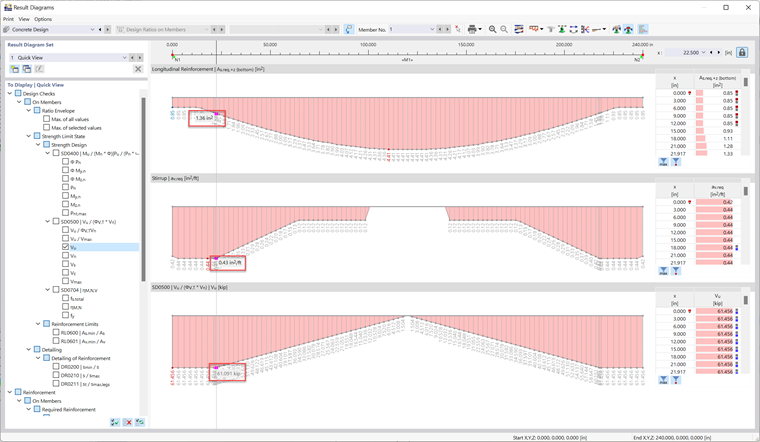
Die Stahlbetonbemessung nach ACI 318-19 [1] kann mit RFEM 6 durchgeführt werden. The Concrete Design Add-on also calculates a required shear reinforcement of 0.43 in²/ft at the distance d from the support (see Image 04).
Hinweis: The results in RFEM 6 differ from the hand calculations slightly due to a more accurate value for the Depth (d) calculated. RFEM 6 berücksichtigt, dass die Zugbewehrung aus mehreren Lagen besteht, während die manuellen Berechnungen von einer einzigen Lage ausgehen.
Abschließend wird noch die maximale Tragfähigkeit der Betondruckstrebe des Schubfachwerkes gemäß Abschnitt 22.5.1.2 überprüft.
61,10 kips ≤ 175,00 kips.
Der Schubnachweis nach ACI 318-19 ist somit erfüllt.
Wie erwartet liefert Gleichung b) einen geringeren Schubwiderstand als Gleichung a).
Zusätzlich ist der Schubwiderstand Vc auf den Maximalwert Vc,max nach 22.5.5.1.1 [1] begrenzt.
Zusammenfassung
Mit ACI 318-19 [1] wurde ein neues Konzept zur Ermittlung des Schubwiderstandes Vc eingeführt. Dabei ist es gelungen, die Vielzahl an möglichen Bemessungsgleichungen aus der Vorgängerversion auf drei Gleichungen zu reduzieren und dabei den Einfluss der Normalspannung, der Bauteilhöhe und des Längsbewehrungsgrades zu berücksichtigen. Dadurch vereinfacht sich die Berechnung des Schubwiderstandes Vc.
,_Table_22.5.5.1,_ACI_318-19.png?mw=760&hash=df344c4cbc6e75e1a5d3e8fc97af7028acef3a2d)
,_Table_22.5.5.1_ACI_318-19.png?mw=760&hash=52b0cc2b9521511642861a07ad54c936a9837db3)