返回知识库

8121x

001450

Sonja von Bloh，硕士

2017-06-12

按照规范 EN 1991-4 计算贮仓漏斗荷载

在上一篇文章中介绍了按照规范 DIN EN 1991-4 对筒仓施加荷载。 Am Beispiel eines freistehenden zylindrischen Silos mit einem konischen Trichter für Zement werden die Fülllasten auf den Trichter berechnet.

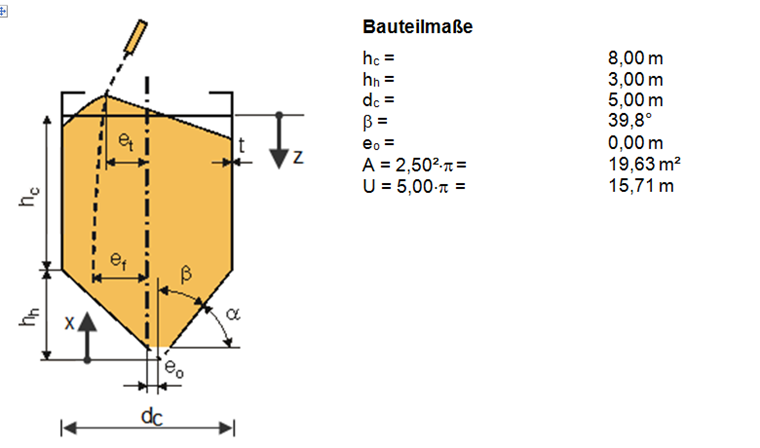
布局和尺寸

结构体系如图01所示。

System und Bauteilmaße des Zementsilos

System und Bauteilmaße des Zementsilos

不同荷载应用的决定性特征值

下表列出了最大料斗压力下适用的颗粒物极值。

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

物理性质

应根据 EN 1991‑4 [1]中 6.1.1(2) 确定筒仓漏斗壁的陡峭程度：

如果土层与水平面的夹角小于 5°，则认为是平土。

浅漏斗是指不属于平的或陡峭的漏斗。

陡峭料斗是指满足以下标准的任何料斗：

\tan β < \frac{1 - K}{2 \cdot μ_{h}} (6.1)

公式 1

\tan 39, 8 ° = 0, 83 > \frac{1 - 0, 450}{2 \cdot 0, 458} = 0, 60

公式 2

该料斗属于浅料斗。

填充荷载

詹森特征深度 z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} (5.75)

公式 3

z_{o} = \frac{1}{0, 450 \cdot 0, 458} \cdot \frac{19, 63}{15, 71} = 6, 07 m

公式 4

垂直距离 h_o
对于对称填充的圆形筒仓，等效实体面与最高实体墙接触点之间的竖向距离 h_o计算如下：

h_{o} = \frac{d_{c}}{6} \cdot \tan ϕ_{r} (5.78)

公式 5

h_{o} = \frac{5, 00}{6} \cdot \tan 36, 00 ° = 0, 61 m

公式 6

参数 n

n = - (1 \tan ϕ_{r}) \cdot (\frac{1 - h_{o}}{z_{o}}) (5.76)

公式 7

n = - (1 \tan 36, 00 °) \cdot (\frac{1 - 0, 61}{6, 07}) = - 1, 55

公式 8

坐标 z
z = h_c = 8.00 m 6.1.2(2)

竖向压力 p_vf

p_{vf} = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}}) (5.79)

公式 9

公式 10

底部荷载放大镜 C_b
Cb = 1.0₍ 6.3)
底部荷载放大系数 C_b适用于作用评估等级 2 的筒仓，前提是所储存的固体不具有动力行为。

料斗过渡区的平均竖向压力
p_vtf = C_b p_vf (6.2)
p_vtf = 1.0 · 69.27 = 69.27 kN/m ²

活动摩擦
在浅料斗中，壁摩擦力没有完全发挥作用。壁面动摩擦系数或有效摩擦系数应按照下式计算：

μ_{heff} = \frac{1 - K}{2 \cdot \tan β} (6.26)

公式 11

μ_{heff} = \frac{1 - 0, 450}{2 \cdot \tan 39, 8 °} = 0, 33

公式 12

参数 n
n = S (1 - b) μ_heff cot β (6.28)
S = 2 (6.9)
n = 2 (1 - 0.2) 0.33 cot 39.8 ° = 0.634

参数_F

F_{f} = 1 - \frac{b}{\frac{1 \tan β}{μ_{heff}}} (6.27)

公式 13

F_{f} = 1 - \frac{0, 2}{\frac{1 \tan 39, 8 °}{0, 33}} = 0, 943

公式 14

参数 n
n = S (F_f μ_heff cot β) - 2 (6.8)
n = 2 · (0.943 · 0.33 · cot 39.8 ° + 0.943) - 2 = 0.634

常压
p_nf (x) = F_f p_v (x) (6.29)

p_{nf} (x) = F_{f} \cdot (γ \cdot \frac{h_{h}}{n - 1} \cdot (\frac{x}{h_{h}} - (\frac{x}{h_{h}})^{n}) p_{vft} \cdot (\frac{x}{h_{h}})^{n}

公式 15

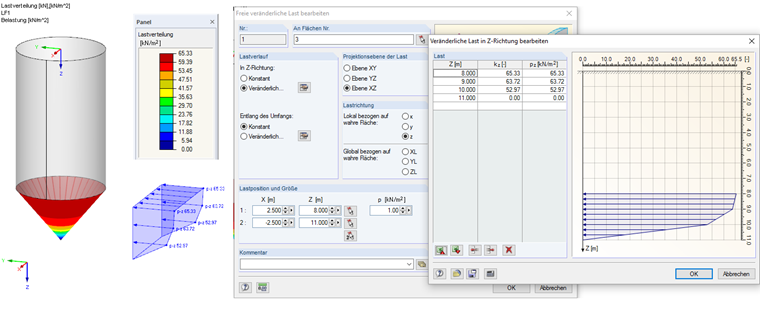
p_nf (0.00) = 0.00 kN/m²
p_nf (1.00) = 52.97 kN/m²
p_nf (2.00) = 63.72 kN/m²
p_nf (3.00) = 65.33 kN/m ²

该荷载可以作为自由可变荷载输入到 RFEM 中。荷载输入如图 03 所示。

Lasten senkrecht auf die Trichterwände pnf

Lasten senkrecht auf die Trichterwände pnf

料斗摩擦力
p_tf (x) = μ_heff F_f p_v (x) (6.30)
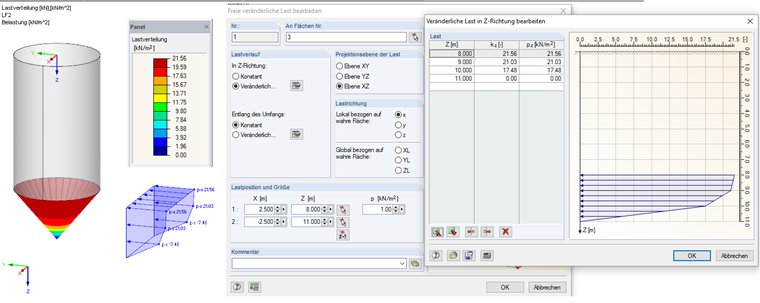
p_tf (0.00) = 0.00 kN/m²
p_tf (1.00) = 0.33 · 52.97 = 17.48 kN/m ²
p_tf (2.00) = 0.33 · 63.72 = 21.03 kN/m ²
p_tf (3.00) = 0.33 · 65.33 = 21.56 kN/m ²

该荷载可以作为自由可变荷载输入到 RFEM 中。荷载输入如图 04 所示。

Reibungslasten im Trichter ptf

Reibungslasten im Trichter ptf

参考

[1] 欧洲规范 1：结构作用 - 第 4 部分：筒仓与水槽； EN 1991‑4:2010‑12

作者

von Bloh 女士为我们的客户提供技术支持，负责 SHAPE-THIN 软件的开发，以及钢结构和铝合金结构的开发。

链接

筒仓与仓库结构设计软件

下载

RFEM Model File

;