8137x

001450

Sonja von Bloh, M.Sc.

12.06.2017

Charges sur une trémie de silo selon EN 1991-4

L'article précédent décrit les actions sur les silos selon DIN EN 1991-4. Am Beispiel eines freistehenden zylindrischen Silos mit einem konischen Trichter für Zement werden die Fülllasten auf den Trichter berechnet.

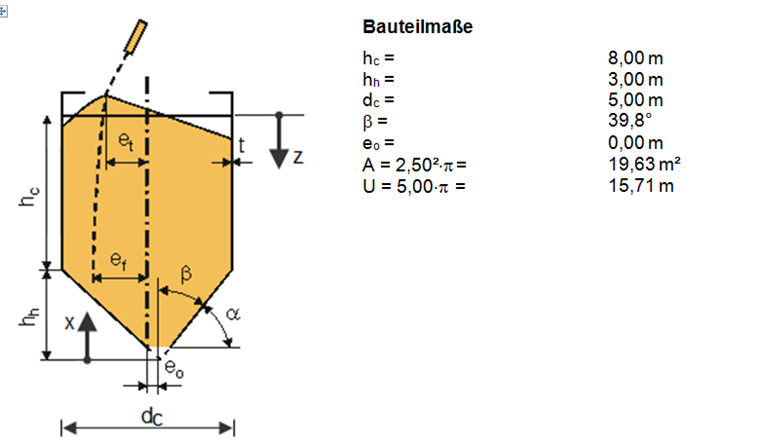
Disposition et dimensions

La Figure 01 représente cette structure.

System und Bauteilmaße des Zementsilos

Valeurs caractéristiques déterminantes pour différentes applications de charge

Les valeurs extrêmes applicables des particules solides pour les pressions maximales de la trémie en condition pleine sont incluses dans le tableau suivant.

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Propriétés physiques

Il convient de déterminer les charges sur les parois des trémies de silos selon l'EN 1991-4 [1] , 6.1.1 (2) en fonction de la pente des parois des trémies selon les classes suivantes :

Un sol plat doit être supposé si l'angle d'inclinaison du sol par rapport à l'horizontale est inférieur à 5°.

Une trémie peu profonde est une trémie qui n'est pas classée comme plate ou à forte pente.

Une trémie à pente raide est une trémie qui satisfait au critère suivant :

\tan β < \frac{1 - K}{2 \cdot μ_{h}} (6.1)

Formule 1

\tan 39, 8 ° = 0, 83 > \frac{1 - 0, 450}{2 \cdot 0, 458} = 0, 60

Formule 2

La trémie est classée comme une trémie peu profonde.

Charges de remplissage

Profondeur caractéristique Janssen z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} (5.75)

Formule 3

z_{o} = \frac{1}{0, 450 \cdot 0, 458} \cdot \frac{19, 63}{15, 71} = 6, 07 m

Formule 4

Distance verticale h_o
Dans le cas d'un silo circulaire rempli symétriquement, la distance verticale h_o entre la surface équivalente du solide et le contact entre le solide et la paroi le plus élevé est calculée comme suit :

h_{o} = \frac{d_{c}}{6} \cdot \tan ϕ_{r} (5.78)

Formule 5

h_{o} = \frac{5, 00}{6} \cdot \tan 36, 00 ° = 0, 61 m

Formule 6

Paramètre n

n = - (1 \tan ϕ_{r}) \cdot (\frac{1 - h_{o}}{z_{o}}) (5.76)

Formule 7

n = - (1 \tan 36, 00 °) \cdot (\frac{1 - 0, 61}{6, 07}) = - 1, 55

Formule 8

Coordonnée z
z = h_c = 8,00 m 6.1.2(2)

Pression verticale p_vf

p_{vf} = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}}) (5.79)

Formule 9

Formule 10

Loupe de charge inférieure C_b
_Cb = 1,0 (6,3)
Le facteur d'amplification de la charge de fond C_b s'applique aux silos de classe d'évaluation de l'action 2 à condition que les solides stockés n'aient pas de comportement dynamique.

Pression verticale moyenne à la transition de la trémie
p_vtf = C_b p_vf (6.2)
p_vtf = 1,0 · 69,27 = 69,27 kN/m ²

Friction mobilisée
Dans une trémie peu profonde, le frottement des parois n'est pas entièrement mobilisé. Le coefficient de frottement mobilisé ou effectif doit être déterminé comme suit :

μ_{heff} = \frac{1 - K}{2 \cdot \tan β} (6.26)

Formule 11

μ_{heff} = \frac{1 - 0, 450}{2 \cdot \tan 39, 8 °} = 0, 33

Formule 12

Paramètre n
n = S (1 - b)_heff cot (6.28)
S = 2 (6,9)
n = 2 (1 - 0,2) 0,33 cot 39,8 ° = 0,634

Paramètre_Ff

F_{f} = 1 - \frac{b}{\frac{1 \tan β}{μ_{heff}}} (6.27)

Formule 13

F_{f} = 1 - \frac{0, 2}{\frac{1 \tan 39, 8 °}{0, 33}} = 0, 943

Formule 14

Paramètre n
n = S (F_f_heff cot β + F) - 2 (6,8)
n = 2 · (0,943 · 0,33 · cot 39,8 ° + 0,943) - 2 = 0,634

Pression normale
p_nf (x) = F_f p_v (x) (6,29)

p_{nf} (x) = F_{f} \cdot (γ \cdot \frac{h_{h}}{n - 1} \cdot (\frac{x}{h_{h}} - (\frac{x}{h_{h}})^{n}) p_{vft} \cdot (\frac{x}{h_{h}})^{n}

Formule 15

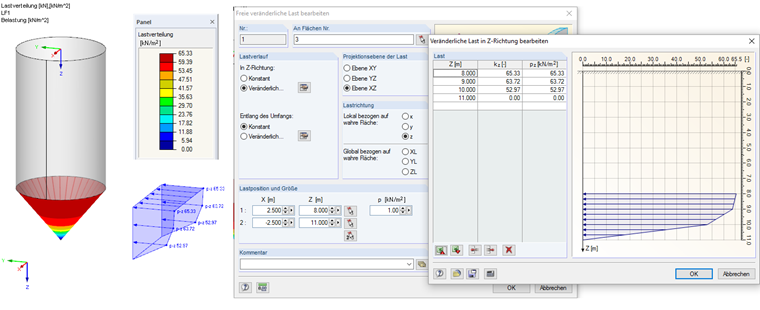
p_nf (0,00) = 0,00 kN/m²
p_nf (1,00) = 52,97 kN/m²
p_nf (2,00) = 63,72 kN/m²
p_nf (3,00) = 65,33 kN/m ²

Cette charge peut être entrée dans RFEM comme une charge variable libre. L'entrée de charge est affichée sur la Figure 03.

Lasten senkrecht auf die Trichterwände pnf

Trémie de traction par friction
p_tf (x) =_heff F_f p_v (x) (6,30)
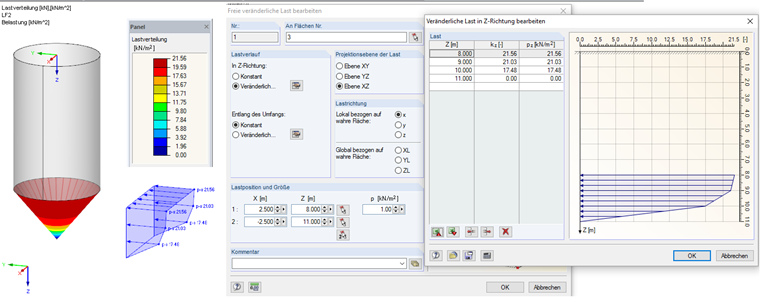
p_tf (0,00) = 0,00 kN/m²
p_tf (1,00) = 0,33 · 52,97 = 17,48 kN/m ²
p_tf (2,00) = 0,33 · 63,72 = 21,03 kN/m ²
p_tf (3,00) = 0,33 · 65,33 = 21,56 kN/m ²

Cette charge peut être entrée dans RFEM comme une charge variable libre. L'entrée de charge est affichée sur la Figure 04.

Reibungslasten im Trichter ptf

Références

[1] Eurocode 1 : Actions sur les structures - Partie 4 : silos et citernes; EN 1991-4:2010-12

Auteur

Mme von Bloh fournit une assistance technique à nos utilisateurs et est également responsable du développement du programme SHAPE-THIN et de la construction en acier et en aluminium.

Liens

Logiciels de calcul de structure pour les silos et les réservoirs de stockage

Téléchargements

Fichier du modèle RFEM

8,48 MB

;