8135x

001450

Sonja von Bloh, M.Sc.

2017-06-12

Нагрузки на силосный бункер по EN 1991-4

В предыдущей статье были описаны воздействия на силос по норме DIN EN 1991-4. Am Beispiel eines freistehenden zylindrischen Silos mit einem konischen Trichter für Zement werden die Fülllasten auf den Trichter berechnet.

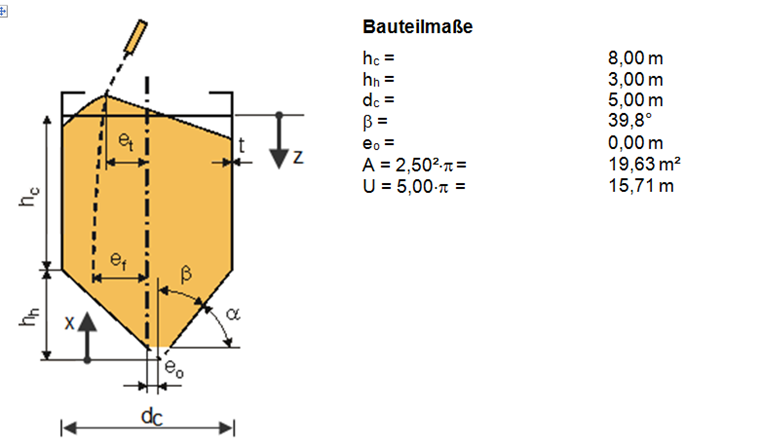
План и размеры

Конструктивная система отображена на Рисунке 01.

System und Bauteilmaße des Zementsilos

Основные нормативные значения для различных приложений нагрузки

Применимые экстремальные значения твердых частиц для максимального давления в бункере в полном состоянии приведены в следующей таблице.

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Физические свойства

Нагрузки на стенки бункеров силоса следует определять по норме EN 1991‑4 [1] , 6.1.1 (2) с учетом крутизны стенок бункера в соответствии со следующими классами:

Считается, что грунт является ровным, если угол наклона грунта по отношению к горизонтали α меньше 5 °.

Неглубоким бункером считается любой бункер, который не классифицируется как плоский или крутой.

Крутым бункером должен быть любой бункер, удовлетворяющий следующему критерию:

\tan β < \frac{1 - K}{2 \cdot μ_{h}} (6.1)

Формула 1

\tan 39, 8 ° = 0, 83 > \frac{1 - 0, 450}{2 \cdot 0, 458} = 0, 60

Формула 2

Бункер классифицируется как неглубокий.

Заполнение нагрузок

Характеристическая высота по Янссену z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} (5.75)

Формула 3

z_{o} = \frac{1}{0, 450 \cdot 0, 458} \cdot \frac{19, 63}{15, 71} = 6, 07 m

Формула 4

Вертикальное расстояние h_o
Для симметрично заполненного круглого силоса вертикальное расстояние h_o между эквивалентной поверхностью тела и наивысшим контактом тела со стенкой рассчитывается следующим образом:

h_{o} = \frac{d_{c}}{6} \cdot \tan ϕ_{r} (5.78)

Формула 5

h_{o} = \frac{5, 00}{6} \cdot \tan 36, 00 ° = 0, 61 m

Формула 6

Параметр n

n = - (1 \tan ϕ_{r}) \cdot (\frac{1 - h_{o}}{z_{o}}) (5.76)

Формула 7

n = - (1 \tan 36, 00 °) \cdot (\frac{1 - 0, 61}{6, 07}) = - 1, 55

Формула 8

Координата z
z = h_c = 8,00 м 6.1.2 (2)

Вертикальное давление p_vf

p_{vf} = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}}) (5.79)

Формула 9

Формула 10

Лупа для нижней нагрузки C_b
C_b = 1,0 (6,3)
Коэффициент увеличения нижней нагрузки C_b применяется к силосам класса оценки воздействий 2 при условии, что хранящиеся твердые тела не склонны к динамическому поведению.

Среднее вертикальное давление на переходе бункера
p_vtf = C_b p_vf (6.2)
p_vtf = 1,0 · 69,27 = 69,27 кН/м ²

Мобилизованное трение
В неглубоком бункере трение волны не мобилизуется полностью. Мобилизованный или эффективный коэффициент трения стенки должен быть определен как:

μ_{heff} = \frac{1 - K}{2 \cdot \tan β} (6.26)

Формула 11

μ_{heff} = \frac{1 - 0, 450}{2 \cdot \tan 39, 8 °} = 0, 33

Формула 12

Параметр n
n = S (1 - b) μ_heff кроватка β (6.28)
S = 2 (6,9)
n = 2 (1 - 0,2) 0,33 детская кроватка 39,8 ° = 0,634

Параметр F_f

F_{f} = 1 - \frac{b}{\frac{1 \tan β}{μ_{heff}}} (6.27)

Формула 13

F_{f} = 1 - \frac{0, 2}{\frac{1 \tan 39, 8 °}{0, 33}} = 0, 943

Формула 14

Параметр n
n = S (F_f μ_heff кроватка β + F) - 2 (6,8)
n = 2 · (0,943 · 0,33 · детская кроватка 39,8 ° + 0,943) - 2 = 0,634

Нормальное давление
p_nf (x) = F_f p_v (x) (6,29)

p_{nf} (x) = F_{f} \cdot (γ \cdot \frac{h_{h}}{n - 1} \cdot (\frac{x}{h_{h}} - (\frac{x}{h_{h}})^{n}) p_{vft} \cdot (\frac{x}{h_{h}})^{n}

Формула 15

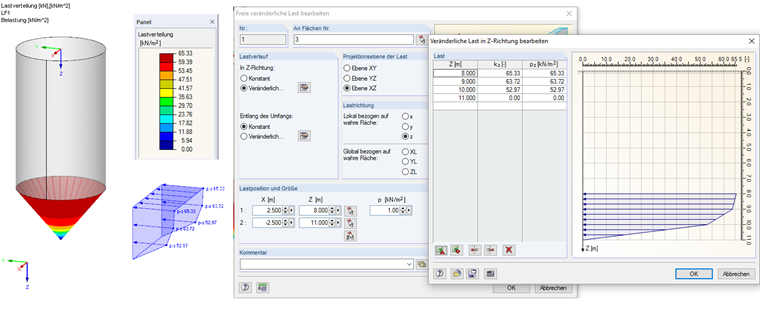
p_nf (0,00) = 0,00 кН/м²
p_nf (1,00) = 52,97 кН/м²
p_nf (2,00) = 63,72 кН/м²
p_nf (3,00) = 65,33 кН/м ²

Эту нагрузку можно задать в программе RFEM как произвольную переменную нагрузку. Ввод нагрузки показан на Рисунке 03.

Lasten senkrecht auf die Trichterwände pnf

Тяга бункера
p_tf (x) = μ_heff F_f p_v (x) (6.30)
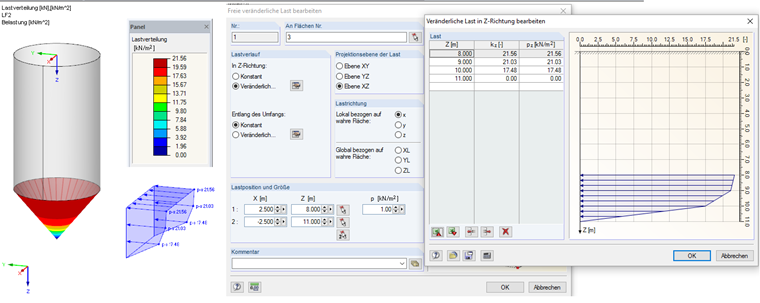
p_tf (0,00) = 0,00 кН/м²
p_tf (1,00) = 0,33 · 52,97 = 17,48 кН/м ²
p_tf (2,00) = 0,33 · 63,72 = 21,03 кН/м ²
p_tf (3,00) = 0,33 · 65,33 = 21,56 кН/м ²

Эту нагрузку можно задать в программе RFEM как произвольную переменную нагрузку. Ввод нагрузки показан на Рисунке 04.

Reibungslasten im Trichter ptf

Ссылки

[1] Еврокод 1: Воздействия на конструкции - Часть 4: Силосы и резервуары; EN 1991‑4: 2010‑12

Автор

Г-жа фон Бло оказывает техническую поддержку нашим клиентам и отвечает за разработку программы SHAPE‑THIN, а также стальных и алюминиевых конструкций.

Ссылки

Программы для расчёта и проектирования силосов и резервуаров

Скачивания

Модель в программе RFEM

8,48 MB

;