8338x

001450

Sonja von Bloh, M.Sc.

12. Juni 2017

Lasten auf Silotrichter nach DIN EN 1991-4

Im diesem Beitrag wurden die Einwirkungen auf Silos nach DIN EN 1991-4 dargestellt. Am Beispiel eines freistehenden zylindrischen Silos mit einem konischen Trichter für Zement werden die Fülllasten auf den Trichter berechnet.

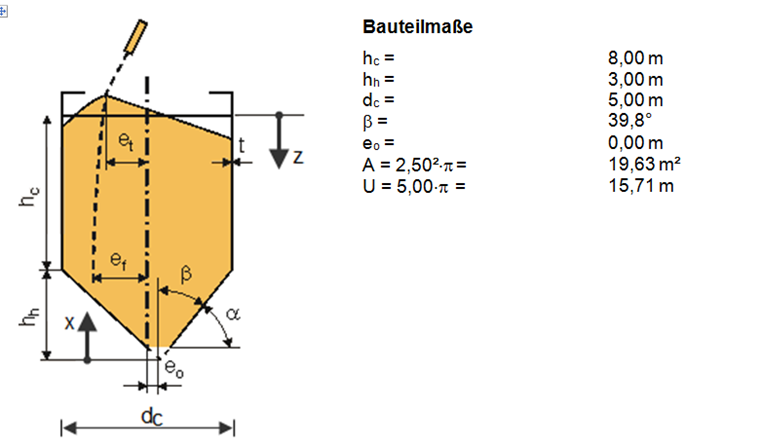
System und Bauteilmaße

Das System ist in Bild 1 dargestellt.

System und Bauteilmaße des Zementsilos

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Die zu verwendenden Extremwerte der Schüttgutkennwerte sind für die maximalen Trichterlasten im Füllzustand in nachstehender Tabelle angegeben.

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Physikalische Kennwerte

Die Lasten auf die Wände von Silotrichtern sind gemäß DIN EN 1991-4 [1], 6.1.1(2) unter Berücksichtigung der Neigung der Trichterwände entsprechend der folgenden Einteilung zu ermitteln:

Von einem ebenen Boden ist auszugehen, wenn der Neigungswinkel des Bodens gegenüber der Horizontalen α weniger als 5° beträgt.

Von einem flach geneigten Trichter ist auszugehen, wenn die beiden anderen angeführten Fälle nicht zutreffen.

Ein steiler Trichter liegt vor, wenn folgendes Kriterium erfüllt ist:

\tan β < \frac{1 - K}{2 \cdot μ_{h}} (6.1)

Formel 1

\tan 39, 8 ° = 0, 83 > \frac{1 - 0, 450}{2 \cdot 0, 458} = 0, 60

Formel 2

Der Trichter ist als flach einzustufen.

Fülllasten

Charakteristische Tiefe z_o nach der Theorie nach Janssen

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} (5.75)

Formel 3

z_{o} = \frac{1}{0, 450 \cdot 0, 458} \cdot \frac{19, 63}{15, 71} = 6, 07 m

Formel 4

Vertikaler Abstand h_o
Der vertikale Abstand h_o zwischen der äquivalenten Schüttgutoberfläche und der höchstgelegenen Kontaktstelle vom gespeicherten Schüttgut mit der Wand ist bei einem symmetrisch gefüllten kreisförmigen Silo anzunehmen mit:

h_{o} = \frac{d_{c}}{6} \cdot \tan ϕ_{r} (5.78)

Formel 5

h_{o} = \frac{5, 00}{6} \cdot \tan 36, 00 ° = 0, 61 m

Formel 6

Parameter n

n = - (1 \tan ϕ_{r}) \cdot (\frac{1 - h_{o}}{z_{o}}) (5.76)

Formel 7

n = - (1 \tan 36, 00 °) \cdot (\frac{1 - 0, 61}{6, 07}) = - 1, 55

Formel 8

Koordinate z
z = h_c = 8,00 m 6.1.2(2)

Vertikallast p_vf

p_{vf} = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}}) (5.79)

Formel 9

p_{vf} = 16, 00 \cdot (0, 61 - \frac{1}{- 1, 55 + 1} \cdot (6, 07 - 0, 61 - \frac{(8, 00 + 6, 07 - 2 \cdot 0, 61)^{- 1, 55 + 1}}{(6, 07 - 0, 61)^{- 1, 55}}) = 69, 27 kN / m ²

Formel 10

Bodenlastvergrößerungsfaktor C_b
C_b = 1,0 (6.3)
Der Bodenlastvergrößerungsfaktor C_b ist bei Silos der Anforderungsklasse 2 unter der Voraussetzung angesetzt worden, dass das gelagerte Schüttgut keine Tendenz zu dynamischem Verhalten aufweist.

Mittlere Vertikallasten am Trichterübergang
p_vtf = C_b · p_vf (6.2)
p_vtf = 1,0 · 69,27 = 69,27 kN/m²

Mobilisierte Reibung
In einem flach geneigten Trichter ist die Wandreibung nicht voll mobilisiert. Der mobilisierte oder effektive Wandreibungskoeffizient sollte angesetzt werden als:

μ_{heff} = \frac{1 - K}{2 \cdot \tan β} (6.26)

Formel 11

μ_{heff} = \frac{1 - 0, 450}{2 \cdot \tan 39, 8 °} = 0, 33

Formel 12

Parameter n
n = S · (1 - b) · μ_heff · cot β (6.28)
S = 2 (6.9)
n = 2 · (1 - 0,2) · 0,33 · cot 39,8° = 0,634

Parameter F_f

F_{f} = 1 - \frac{b}{\frac{1 \tan β}{μ_{heff}}} (6.27)

Formel 13

F_{f} = 1 - \frac{0, 2}{\frac{1 \tan 39, 8 °}{0, 33}} = 0, 943

Formel 14

Parameter n
n = S · (F_f · μ_heff · cot β + F) - 2 (6.8)
n = 2 · (0,943 · 0,33 · cot 39,8° + 0,943) - 2 = 0,634

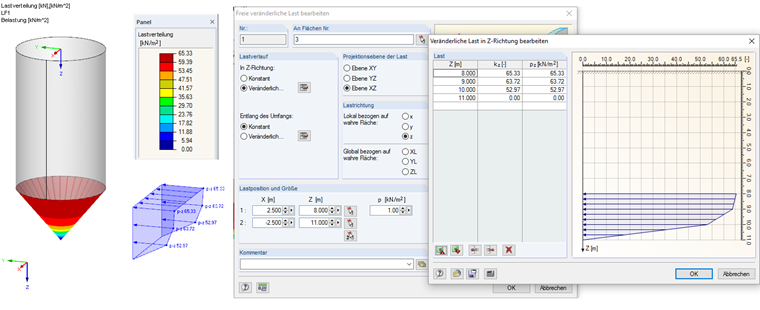
Lasten senkrecht auf die Trichterwände
p_nf(x) = F_f · p_v(x) (6.29)

p_{nf} (x) = F_{f} \cdot (γ \cdot \frac{h_{h}}{n - 1} \cdot (\frac{x}{h_{h}} - (\frac{x}{h_{h}})^{n}) p_{vft} \cdot (\frac{x}{h_{h}})^{n}

Formel 15

p_nf(0,00) = 0,00 kN/m²
p_nf(1,00) = 52,97 kN/m²
p_nf(2,00) = 63,72 kN/m²
p_nf(3,00) = 65,33 kN/m²

Diese Last kann in RFEM als freie veränderliche Last eingegeben werden. Die Lasteingabe kann dem Bild 3 entnommen werden.

Lasten senkrecht auf die Trichterwände pnf

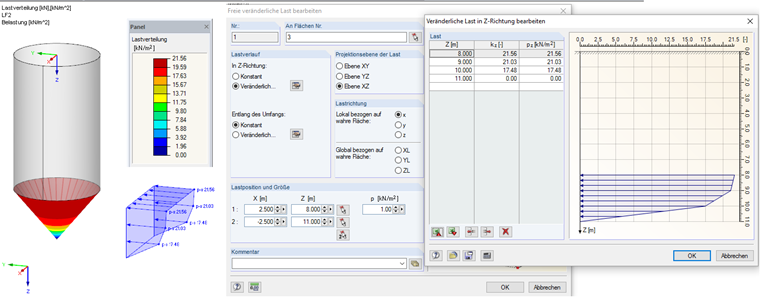
Reibungslasten im Trichter
p_tf(x) = μ_heff · F_f · p_v(x) (6.30)
p_tf(0,00) = 0,00 kN/m²
p_tf(1,00) = 0,33 · 52,97 = 17,48 kN/m²
p_tf(2,00) = 0,33 · 63,72 = 21,03 kN/m²
p_tf(3,00) = 0,33 · 65,33 = 21,56 kN/m²

Diese Last kann in RFEM als freie veränderliche Last eingegeben werden. Die Lasteingabe kann dem Bild 4 entnommen werden.

Reibungslasten im Trichter ptf

Literatur

[1] Eurocode 1: Einwirkungen auf Tragwerke - Teil 4: Einwirkungen auf Silos und Flüssigkeitsbehälter; EN 1991-4:2010-12

Autor

Frau von Bloh bietet im Kundensupport Hilfestellung für unsere Anwender und ist zudem für die Entwicklung des Programms RSECTION sowie für den Stahl- und Aluminiumbau zuständig.

Links

Statiksoftware für Silos und Speicherbehälter

Downloads

RFEM-Modelldatei

8,48 MB

;