8137x

001450

Sonja von Bloh, M.Sc.

12.6.2017

Zatížení výsypek podle EN 1991-4

Tématem našeho předchozího článku byla zatížení zásobníků podle EN 1991-4. Na příkladu samostatně stojícího válcového zásobníku na cement s kuželovitou výsypkou nyní předvedeme výpočet tlaků ve výsypce při plnění.

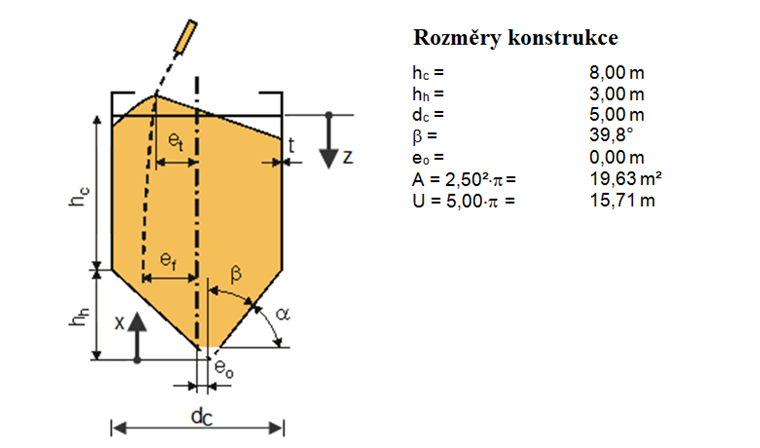
Konstrukce a její rozměry

Konstrukce je znázorněna na obr. 01.

System und Bauteilmaße des Zementsilos

Hodnoty vlastností, které je třeba uvažovat pro různá hodnocení zatížení stěn

Extrémní hodnoty vlastností zrnitých tuhých látek, které se mají uvažovat pro maximální zatížení výsypky při plnění, jsou uvedeny v následující tabulce.

Maßgebliche Kennwerte für die unterschiedlichen Lastansätze

Fyzikální vlastnosti

Zatížení stěn výsypek zásobníků se má určit v souladu s EN 1991-4 [1], 6.1.1(2) podle strmosti stěn výsypky, rozlišené do těchto tříd:

ploché dno má odklon α od vodorovné roviny menší než 5°;

mělká výsypka je jakákoliv výsypka, která není klasifikována jako ploché dno ani jako strmá výsypka;

strmá výsypka je jakákoliv výsypka, která splňuje tuto podmínku:

\tan β < \frac{1 - K}{2 \cdot μ_{h}} (6.1)

Vzorec 1

\tan 39, 8 ° = 0, 83 > \frac{1 - 0, 450}{2 \cdot 0, 458} = 0, 60

Vzorec 2

Tuto výsypku lze klasifikovat jako ploché dno.

Zatížení při plnění

Janssenova charakteristická hloubka z_o

z_{o} = \frac{1}{K \cdot μ} \cdot \frac{A}{U} (5.75)

Vzorec 3

z_{o} = \frac{1}{0, 450 \cdot 0, 458} \cdot \frac{19, 63}{15, 71} = 6, 07 m

Vzorec 4

Svislá vzdálenost h_o
Svislá vzdálenost h_o mezi ekvivalentním povrchem a nejvyšším bodem styku skladované látky se stěnou se u souměrně plněného kruhového zásobníku stanoví takto:

h_{o} = \frac{d_{c}}{6} \cdot \tan ϕ_{r} (5.78)

Vzorec 5

h_{o} = \frac{5, 00}{6} \cdot \tan 36, 00 ° = 0, 61 m

Vzorec 6

Parametr n

n = - (1 \tan ϕ_{r}) \cdot (\frac{1 - h_{o}}{z_{o}}) (5.76)

Vzorec 7

n = - (1 \tan 36, 00 °) \cdot (\frac{1 - 0, 61}{6, 07}) = - 1, 55

Vzorec 8

Souřadnice z
z = h_c = 8,00 m 6.1.2(2)

Svislý tlak p_vf

p_{vf} = γ \cdot (h_{o} - \frac{1}{n 1} \cdot (z_{o} - h_{o} - \frac{(z z_{o} - 2 \cdot h_{o})^{n 1}}{(z_{o} - h_{o})^{n}}) (5.79)

Vzorec 9

Vzorec 10

Součinitel zvyšující zatížení dna C_b
C_b = 1,0 (6.3)
Součinitel zvyšující zatížení dna C_b se u zásobníků třídy 2 uvažuje za předpokladu, že skladovaná látka nemá při vyprazdňování zásobníku sklon k dynamickému chování.

Průměrný svislý tlak na přechodu mezi svislou částí stěny zásobníku a výsypkou
p_vtf = C_b · p_vf (6.2)
p_vtf = 1,0 · 69,27 = 69,27 kN/m²

Účinné tření
V mělkých výsypkách není tření o stěnu plně mobilizováno. Součinitel účinného tření o stěnu se má stanovit takto:

μ_{heff} = \frac{1 - K}{2 \cdot \tan β} (6.26)

Vzorec 11

μ_{heff} = \frac{1 - 0, 450}{2 \cdot \tan 39, 8 °} = 0, 33

Vzorec 12

Parametr n
n = S · (1 - b) · μ_heff · cot β (6.28)
S = 2 (6.9)
n = 2 · (1 - 0,2) · 0,33 · cot 39,8° = 0,634

Parametr F_f

F_{f} = 1 - \frac{b}{\frac{1 \tan β}{μ_{heff}}} (6.27)

Vzorec 13

F_{f} = 1 - \frac{0, 2}{\frac{1 \tan 39, 8 °}{0, 33}} = 0, 943

Vzorec 14

Parametr n
n = S · (F_f · μ_heff · cot β + F) - 2 (6.8)
n = 2 · (0,943 · 0,33 · cot 39,8° + 0,943) - 2 = 0,634

Tlak kolmý ke stěně výsypky
p_nf(x) = F_f · p_v(x) (6.29)

p_{nf} (x) = F_{f} \cdot (γ \cdot \frac{h_{h}}{n - 1} \cdot (\frac{x}{h_{h}} - (\frac{x}{h_{h}})^{n}) p_{vft} \cdot (\frac{x}{h_{h}})^{n}

Vzorec 15

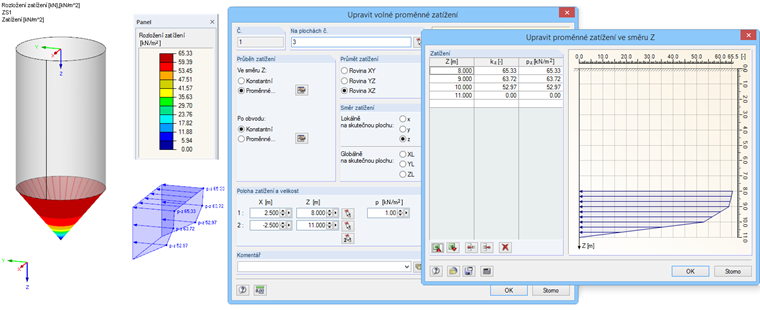
p_nf(0,00) = 0,00 kN/m²
p_nf(1,00) = 52,97 kN/m²
p_nf(2,00) = 63,72 kN/m²
p_nf(3,00) = 65,33 kN/m²

Toto zatížení lze v programu RFEM zadat jako volné proměnné zatížení. Zadání zatížení je znázorněno na obr. 03.

Lasten senkrecht auf die Trichterwände pnf

Tahová složka tření ve výsypce
p_tf(x) = μ_heff · F_f · p_v(x) (6.30)
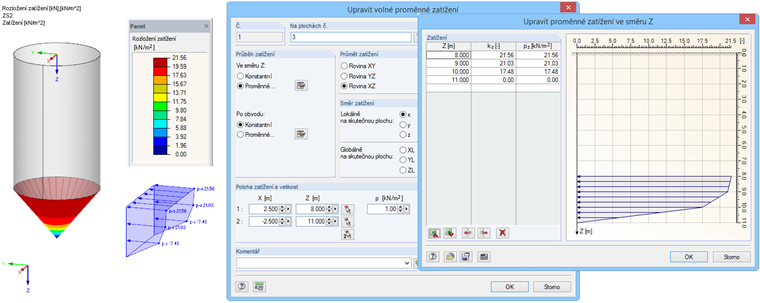
p_tf(0,00) = 0,00 kN/m²
p_tf(1,00) = 0,33 · 52,97 = 17,48 kN/m²
p_tf(2,00) = 0,33 · 63,72 = 21,03 kN/m²
p_tf(3,00) = 0,33 · 65,33 = 21,56 kN/m²

Toto zatížení lze v programu RFEM zadat jako volné proměnné zatížení. Zadání zatížení je znázorněno na obr. 04.

Reibungslasten im Trichter ptf

Literatura

[1] Eurokód 1: Zatížení konstrukcí - Část 4: Zatížení zásobníků a nádrží; ČSN EN 1991-4:2008

Autor

Ing. von Bloh zajišťuje technickou podporu zákazníkům a je zodpovědná za vývoj programu RSECTION a addonů pro ocelové a hliníkové konstrukce.

Odkazy

Software pro návrh a analýzu sil, vodojemů a zásobních nádrží

Stahování

Model pro zkušební výpočet

8,48 MB

;