O método de integração predefinido no RFEM é uma {%}#gauss-lobatto Gauss-Lobatto quadratura]] com nove pontos de integração. Esta configuração padrão é suficiente para a maioria dos casos. Para representar diagramas de tensão-deformação não lineares com uma precisão suficiente (por exemplo, no caso de betão armado com fibra de aço), pode ser útil aumentar o número de pontos de integração. Portanto, quando utiliza um material não linear , é possível personalizar o número de pontos de integração em cada camada entre 3 e 99 pontos (ver imagem Ajustar pontos de integração para camadas ). Tenha em atenção, que um maior número de pontos de integração resulta num tempo de cálculo mais longo.
Além disso, estão disponíveis três métodos de integração diferentes para seleção (ver figura Especificação do método de integração ):
- Quadratura de Gauss-Lobatto
- Regra de Simpson
- Regra do trapézio
Estes métodos de integração, também conhecidos como fórmulas de quadratura, são explicados a seguir. Em geral, pode assumir-se que a quadratura de Gauss-Lobatto com um número fixo de pontos de integração providencia a mais elevada precisão sem aumentar significativamente o esforço computacional. A regra trapezoidal ou a regra de Simpson' apenas conduz a um resultado melhor em casos especiais.
Fórmulas de quadratura
O objetivo da fórmula de quadratura é calcular uma aproximação numérica de uma integral. Para isso, são selecionados pontos de apoio no domínio de integração e as avaliações da função ponderada são adicionadas nesses pontos. O cálculo de um momento é utilizado como exemplo para as seguintes explicações.
d é a altura de qualquer camada numa superfície multicamada. O programa tenta então aproximar a integral da seguinte forma:
Para isso, selecione n pontos da grelha -d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 sobre a altura da camada, bem como nos pesos escalares ω1, . . . , ωn são necessários específicos da respectiva fórmula de quadratura.
O RFEM utiliza sempre um número singular n = 2k + 1 de pontos de grelha e pelo menos a parte superior, o meio e a parte inferior da camada são selecionadas como pontos de integração. Assim, resulta em z1 = -d/2, zk = 0 e zn = d/2. Isto é necessário para que os valores das tensões nestas posições possam ser calculados com precisão e depois apresentados no programa. Se definir um número par de pontos de grelha, é utilizado para o cálculo o número singular imediatamente seguinte.
O grau de precisão de uma fórmula de quadratura é dado pela sua ordem p. Este é o grau mais alto de um polinómio, que está integrado exatamente.
Regra do trapézio
Um exemplo simples de uma fórmula de quadratura é a regra do trapézio. Neste caso, as duas bordas exteriores do domínio de integração são selecionadas como posições de apoio; ou seja, z1 = -d/2 e z2 = d/2. A regra trapezoidal é de primeira ordem, uma vez que as funções lineares são integradas exatamente, mas as funções quadráticas não.
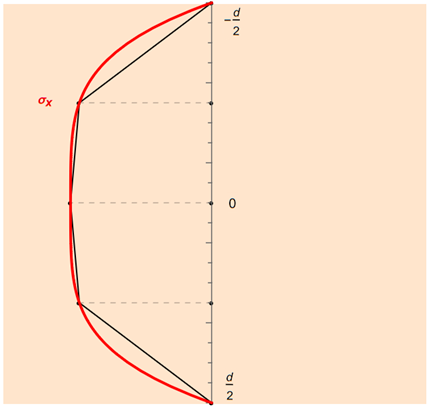
No caso da variante da regra trapezoidal cumulativa utilizada no RFEM, se selecionar n pontos de integração, o intervalo de integração é dividido equidistantemente em n - 1 intervalos parciais e a regra trapezoidal é aplicada a cada um deles.
A figura seguinte mostra um exemplo da regra trapezoidal resumida para cinco pontos de integração.
Regra de Simpson
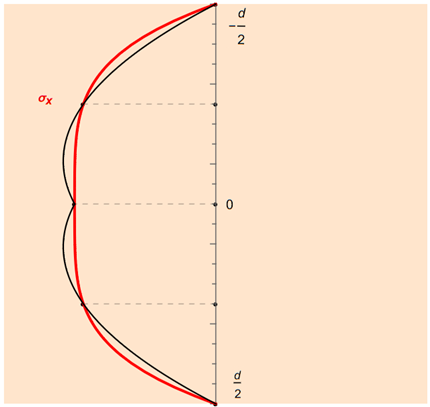
A regra de Simpson' é uma fórmula de quadratura de terceira ordem que utiliza três pontos de integração, dois nas bordas e um no centro da região de integração. Os pesos são selecionados de tal forma que a solução aproximada corresponde à integral sobre uma parábola que passa por esses três pontos. Com z1 = -d/2, z2 = 0 e z3 = d/2, obtemos a forma:
O RFEM também utiliza aqui uma quadratura composta. Se existe um número singular n de pontos de apoio, (n - 1)/2 intervalos parciais igualmente longos são obtidos, aos quais a regra de Simpson pode ser aplicada. A figura mostra isso novamente como um exemplo para cinco pontos de integração.
Quadratura de Gauss-Lobatto
Na quadratura de Gauss-Lobatto, os dois pontos de fronteira z1 = -d/2 e zn = d/2 são sempre especificados como posições de apoio e todos os outros pontos de integração são selecionados de tal forma que é alcançada a ordem mais elevada possível. sendo p = 2n - 3. Para n = 3, a quadratura de Gauss-Lobatto é equivalente à regra de Simpson'; para n = 5, por exemplo: