Manuais online RFEM 6 | Superfícies multicamada

Voltar para manuais online

2262x

003626

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2023-10-19

Selecionar manual

Vista geral

Módulo Superfícies multicamadas

Teoria

Entradas

Resultados

Exemplos de cálculo

Rigidezes para superfícies multicamadas

Modelos de Materiais

A base para a composição de superfícies multicamadas em uma rigidez de superfície efetiva são os modelos de materiais. Com o Add-On Superfícies Multicamadas, os modelos de materiais podem ser combinados livremente no programa RFEM 6. As bases dos modelos de materiais estão descritas nos capítulos Materiais e Comportamento de Material Não Linear do manual do RFEM.

Uma seleção de possibilidades de combinação dos modelos de materiais está configurada no modelo "Modelos Multicamadas" (ver coluna direita), que você pode baixar para estudo adicional das combinações.

A lista a seguir mostra uma seleção de combinações possíveis:

Camadas isotrópicas (por exemplo, concreto - aço)
Camadas ortotrópicas (por exemplo, madeira laminada cruzada)
Isotrópico - ortotrópico (por exemplo, aço - GFRP)
Isotrópico Plástico - Isotrópico (por exemplo, concreto - aço)
Isotrópico Não Linear Elástico - Ortotrópico (por exemplo, concreto - madeira)
Isotrópico - Ortotrópico Plástico (por exemplo, concreto - madeira)
Isotrópico Dano - Ortotrópico (por exemplo, concreto - madeira)

Informação

Para a combinação de materiais não lineares, o Add-On Comportamento de Material Não Linear deve estar ativado.

Rigidezes em superfícies multicamadas sem volume

A variante de cálculo mais simples no Add-On Superfícies Multicamadas é definir diferentes camadas de superfície no tipo de espessura 'Camadas' sem volume. Mas aqui também os modelos de materiais podem ser combinados livremente.

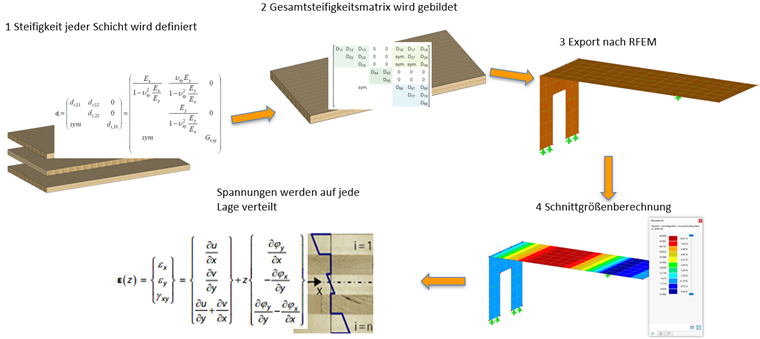
Uma vez definidas as camadas, o Add-On Superfícies Multicamadas gera uma matriz de rigidez global para a superfície. No RFEM, são calculados esforços internos e deformações para essa superfície. No respectivo Add-On de dimensionamento, como Dimensionamento de Madeira ou Cálculo de Tensão-Deformação, esses esforços internos são então divididos nas camadas disponíveis. Normalmente, os esforços internos são apresentados em três pontos de integração por camada.

Processo de cálculo de superfícies multicamada

A seguir, é explicada a determinação da matriz de rigidez para material isotrópico e ortotrópico.

Cálculo da Matriz de Rigidez

As condições básicas dos modelos de materiais são as seguintes (ver também o capítulo Materiais do manual do RFEM):

Todos os valores de rigidez ≥ 0
A matriz de rigidez total da superfície deve ser definida positivamente.
Equação básica Isotrópica:

E = 2 G (1 + ν)

E	Módulo de elasticidade.
G	módulo de corte
ν	Coeficiente de Poisson

Módulo de elasticidade, módulo de corte e relação de Poisson ' s

Equação básica Ortotrópica:

\frac{ν_{y x}}{E_{y}} = \frac{ν_{x y}}{E_{x}}

Relação de deformação transversal

Matriz de Rigidez Local de Cada Camada

Isotrópico

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{i}}{1 - ν_{i}^{2}} & \frac{ν_{i} E_{i}}{1 - ν_{i}^{2}} & 0 \\ \frac{E_{i}}{1 - ν_{i}^{2}} & 0 \\ s y m . & G_{i} \end{matrix}] i = 1, . . ., n m i t G_{i} = \frac{E_{i}}{2 (1 + ν_{i})}

Rigidez camada de matriz isotrópica

Ortotrópico

d_{i}' = [\begin{matrix} d'_{11, i} & d'_{12, i} & 0 \\ d'_{22, i} & 0 \\ s y m . & d'_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{x y, i} E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{x y, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ s y m . & G_{x y, i} \end{matrix}] i = 1, . . ., n

Rigidez camada de matriz ortotrópica

Informação

Para material ortotrópico, o módulo de cisalhamento no plano (G_xy) é definido por valores de material, enquanto que para material isotrópico é determinado a partir do módulo de elasticidade e da relação de Poisson. Portanto, para material ortotrópico, a relação de compressão transversal com o princípio "localização-causa" é importante.

As rigidezes ao cisalhamento para material ortotrópico são as seguintes:

G_xy	Módulo de cisalhamento no plano (por exemplo, 690 N/mm² para C24)
G_xz	Módulo de cisalhamento na direção x através da espessura (por exemplo, 690 N/mm² para C24)
G_yz	Módulo de cisalhamento na direção y através da espessura (por exemplo, 690 N/mm² para C24) – também denominado "módulo de rolamento"

Para material ortotrópico, a peculiaridade adicional é que rigidezes direcionais podem ser definidas em uma superfície. No caso padrão, a orientação local da superfície ou camada na direção x corresponde à rigidez na direção x. No entanto, como esta pode ser definida livremente pelo ângulo β no tipo de espessura 'Camadas', é necessário transformar as rigidezes adequadamente.

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & d_{13, i} \\ d_{22, i} & d_{23, i} \\ s y m . & d_{33, i} \end{matrix}] = T_{3 x 3, i}^{T} d'_{i} T_{3 x 3, i}

Rigidez de transformação

T_{3 x 3, i} = [\begin{matrix} c ² & s ² & c s \\ s ² & c ² & - c s \\ - 2 c s & 2 c s & c ² - s ² \end{matrix}] m i t c = \cos (β_{i}), s = \sin (β_{i})

Matriz de transformação

Elemento acumulado de cada camada:

d_{11, i} = c^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + s^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{12, i} = c^{2} s^{2} d'_{11, i} + s^{4} d'_{12, i} + c^{4} d'_{12, i} + c ² s ² d'_{22, i} - 4 c ² s ² d'_{33, i}

d_{13, i} = c^{3} s d'_{11, i} + c s^{3} d'_{12, i} - c^{3} s d'_{12, i} - c s^{3} d'_{22, i} - 2 c^{3} s d'_{33, i} + 2 c s^{3} d'_{33, i}

d_{22, i} = s^{4} d'_{11, i} + 2 c ² s ² d'_{12, i} + c^{4} d'_{22, i} + 4 c ² s ² d'_{33, i}

d_{23, i} = c s^{3} d'_{11, i} + c^{3} s d'_{12, i} - c s^{3} d'_{12, i} - c^{3} s d'_{22, i} + 2 c^{3} s d'_{33, i} - 2 c s^{3} d'_{33, i}

d_{33, i} = c^{2} s^{2} d'_{11, i} - 2 c ² s ² d'_{12, i} + c^{2} s^{2} d'_{22, i} + {(c^{2} - s^{2})}^{2} d'_{33, i}

Condições individuais por turno

Elementos de Flexão e Torção [Nm]

Os elementos da matriz para flexão e torção são fornecidos nas equações a seguir.

D_{11} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{11, i}

Rigidez de flexão em x

D_{12} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{12, i}

Termo de excentricidade (12)

D_{22} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{22, i}

Rigidez à flexão em y

D_{13} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{13, i}

Termo de excentricidade (13)

D_{23} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{23, i}

Termo de excentricidade (23)

D_{33} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{3} - z_{m i n, i}^{3}}{3} d_{33, i}

Rigidez à rotação

Com apenas uma camada no tipo de espessura 'Camadas', o cálculo é realizado de acordo com as equações explicadas no manual do RFEM.

Para cisalhamento (elementos D44/55), diferentes equações são aplicáveis no tipo de espessura 'Camadas'. Elas são apresentadas na seção Cisalhamento no Plano da Lâmina.

Termos de Excentricidade [Nm/m]

Placas assimétricas produzem termos de excentricidade. Uma superfície assimétrica pode ocorrer, por exemplo, no cálculo de resistência ao fogo devido a uma queima unilateral de uma placa de madeira laminada cruzada. Os elementos da matriz são os seguintes:

D_{16} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{11, i}

Elemento de excentricidade D16

D_{17} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{12, i}

Elemento de excentricidade D17

D_{18} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{13, i}

Excentricidade Elemento D18

D_{27} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{22, i}

Elemento de excentricidade D27

D_{28} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{23, i}

Elemento de excentricidade D28

D_{38} = \sum_{i = 1}^{n} \frac{z_{m a x, i}^{2} - z_{m i n, i}^{2}}{2} d_{33, i}

Elemento de excentricidade D38

Plano da Lâmina [N/m]

No plano da lâmina, as rigidezes normais no plano da lâmina são tratadas. O elemento D88 calcula o cisalhamento no plano da lâmina – ou seja, a força transversal na lâmina. Os elementos da matriz são os seguintes:

D_{66} = \sum_{i = 1}^{n} t_{i} d_{11, i}

Rigidez axial x D66

D_{67} = \sum_{i = 1}^{n} t_{i} d_{12, i}

Rigidez normal excêntrico D67

D_{68} = \sum_{i = 1}^{n} t_{i} d_{13, i}

Rigidez normal excêntrico D68

D_{77} = \sum_{i = 1}^{n} t_{i} d_{22, i}

Rigidez axial y D77

D_{78} = \sum_{i = 1}^{n} t_{i} d_{23, i}

Rigidez normal excêntrico D78

D_{88} = \sum_{i = 1}^{n} t_{i} d_{33, i}

Corte de placa D88

Cisalhamento no Plano da Lâmina [N/m]

Para determinar a rigidez ao cisalhamento de um material ortotrópico, as rigidezes devem ser rotacionadas conforme a orientação em relação ao eixo local da superfície. Isso deve ser feito para cada camada do tipo de espessura 'Camadas'. Com uma construção simples de camadas com orientação de 0° da camada externa e orientação de 90° da camada subjacente, resulta uma grande flexibilidade ao cisalhamento, que deve ser considerado adequadamente no modelo multicamadas. Na imagem a seguir (fonte [1]), isso é ilustrado por exemplo em uma placa de madeira laminada cruzada.

Ilustração de deformação de corte em madeira laminada cruzada, fornecida pelo Information Service Timber.

Deformação de corte (Fonte: Informationsdienst Holz)

Na teoria de laminados, a rigidez ao cisalhamento de uma construção em camadas é calculada por meio da transformação de todas as componentes de flexão e cisalhamento nas respectivas direções de cada camada. Mais informações estão disponíveis nas literaturas indicadas abaixo.

Visualização da orientação dos eixos de rigidez num laminado para otimizar as propriedades do material.

Orientação de rigidez

Através da transformação de rigidez mostrada na imagem, as rigidezes são somadas. Essa adição é também conhecida como "Integral de Grashoff".

D_{44, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{22}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{x}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{x}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidez de corte na direção x

Para o cálculo da rigidez na direção x e y, é calculado para cada construção de superfície multicamada um chamado ponto de rigidez.

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{x}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro de rigidez em x

D_{55, c a l c}^{"} = \frac{1}{\int_{- t / 2}^{t / 2} \frac{G_{11}^{"} (z)}{G_{11}^{"} (z) G_{22}^{"} (z) - {G_{12}^{"}}^{2} (z)} {(\frac{\int_{z}^{t / 2} E_{y}^{"} (\bar{z}) (\bar{z} - z_{0, x}) d \bar{z}}{\int_{- t / 2}^{t / 2} E_{y}^{"} (\bar{z}) {(\bar{z} - z_{0, x})}^{2} d \bar{z}})}^{2} d z}

Rigidez ao corte na direção y

Ponto de rigidez na direção y:

z_{0, x} = \frac{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) z d z}{\int_{- t / 2}^{t / 2} E_{y}^{"} (z) d z} = \frac{I_{1}}{I_{0}}

Centro de rigidez na direção y

Para capturar a orientação por camada na determinação da rigidez ao cisalhamento, as rigidezes são calculadas conforme as equações a seguir.

G_{11, i}^{"} = \cos^{2} (φ - ß_{i}) G_{x z, i} + \sin^{2} (φ - ß_{i}) G_{y z, i}

Rigidez ao corte orientado G11

G representa a rigidez ao cisalhamento das camadas para evitar confusão com os elementos da matriz de rigidez (D).

A rigidez ao cisalhamento de cada camada pode também ser apresentada na forma de matriz como segue:

[\begin{matrix} G_{11} & G_{12} \\ G_{21} & G_{22} \end{matrix}]

Matriz de rigidez ao corte

G_{22, i}^{"} = \sin^{2} (φ - ß_{i}) G_{x z, i} + \cos^{2} (φ - ß_{i}) G_{y z, i}

Rigidez ao corte orientado G22

A rigidez ao cisalhamento excêntrica na seguinte equação seria sempre nula para a construção simétrica mencionada inicialmente de uma madeira laminada cruzada (0°/90°/0°) e, portanto, não relevante. Para uma madeira laminada diagonalmente colada, por exemplo, DLT (Diagonal Laminated Timber), este termo de excentricidade não é nulo e desempenha um papel importante.

G_{12}^{"} = (G_{x z, i} - G_{y z, i}) \sin (φ - ß_{i}) \cos (φ - ß_{i})

Rigidez ao corte orientado excentricamente G12

Mais informações podem ser encontradas, entre outros, em [4] e em um vídeo no YouTube.

Cálculo da Rigidez ao Cisalhamento

A rigidez ao cisalhamento é determinada nos seguintes passos:

Primeiro, é determinado o ângulo de rigidez máxima. O ângulo φ indica a mudança do sistema de coordenadas local x da superfície em relação à direção orientada x''.
Todas as rigidezes são giradas na direção orientada x'', conforme as equações apresentadas acima.
A matriz de rigidez da lâmina de cada camada (3 x 3) é transformada do sistema de coordenadas local x', y' para o sistema rotacionado x'', y". Adicionalmente ao cálculo da rigidez dirigida de cada camada, isso também é feito para os módulos de elasticidade de cada camada.

$E_{x, i}^{"} = d_{12, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{22, i}^{"} {(d_{13, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{22, i}^{"} d_{33, i}^{"} - {(d_{23, i}^{"})}^{2}}$

Módulo de elasticidade orientado na direção x

$E_{y, i}^{"} = d_{22, i}^{"} + \frac{2 d_{12, i}^{"} d_{13, i}^{"} d_{23, i}^{"} - d_{11, i}^{"} {(d_{23, i}^{"})}^{2} - d_{33, i}^{"} {(d_{12, i}^{"})}^{2}}{d_{11, i}^{"} d_{33, i}^{"} - {(d_{13, i}^{"})}^{2}}$

Módulo de elasticidade orientado na direção y
A rigidez ao cisalhamento é calculada com as equações descritas acima (Integral de Grashoff). A rigidez ao cisalhamento é calculada sobre os componentes individuais.

$I = \int_{- h / 2}^{h / 2} d_{11} (z) {(z - z_{0, x})}^{2} d z = \sum_{i = 1}^{n} d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{3} - {(z_{m i n, i} - z_{0, x})}^{3}}{3}$

Momento de inércia na direção x

$χ_{i} = d_{11, i} \frac{{(z_{m a x, i} - z_{0, x})}^{2}}{2} + \sum_{k = i + 1}^{n} d_{11, k} \frac{{(z_{m a x, i} - z_{0, x})}^{2} - {(z_{m i n, i} - z_{0, x})}^{2}}{2}$

Rigidez equivalente por camada (em x)

Aqui, as equações são mostradas apenas para a direção x (D44). O mesmo se aplica à direção y. A rigidez equivalente (componente de Steiner) é calculada para cada camada.
Finalmente, as rigidezes calculadas para a direção orientada de uma construção total são re-calculadas através das relações angulares e apresentadas como rigidezes originais D44, D55 e D45 na matriz de rigidez.

$D_{44} = \cos^{2} (φ) D_{44}^{"} + \sin^{2} (φ) D_{55}^{"}$

Rigidez ao corte recalculada D44

$D_{55} = \sin^{2} (φ) D_{44}^{"} + \cos^{2} (φ) D_{55}^{"}$

Rigidez ao corte recalculada D55

$D_{45} = \sin (φ) \cos (φ) (D_{44}^{"} - D_{55}^{"})$

Rigidez ao corte recalculada D45

Aumento da Rigidez ao Cisalhamento

Como na modelagem de laminados como uma superfície, também são possíveis geometrias com tiras de superfície muito estreitas, quando da análise dessas geometrias problemáticas, a rigidez ao cisalhamento deve ser aumentada adequadamente.

Na equação a seguir, isso é mostrado para a direção X

D_{44}^{"} = \max (D_{44, calc}^{"}, \frac{48}{5 l ²} \frac{1}{\frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{t_{i}^{3}}{12}} - \frac{1}{\sum_{i = 1}^{n} E_{x, i}^{"} \frac{z_{\max, i}^{3} - z_{\min, i}^{3}}{3}}})

Resistência ao corte máxima

O comprimento l na equação acima significa aqui o comprimento mais curto de uma caixa que pode ser colocada sobre a geometria correspondente.

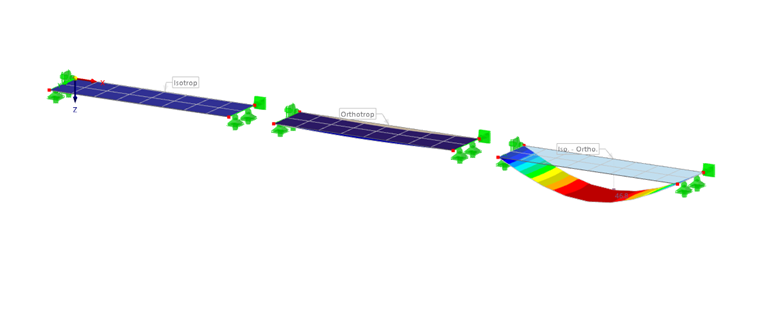
Em outro modelo, que pode ser baixado no lado direito, uma superfície estreita de largura de 10 cm foi comparada com uma superfície idêntica de 20 cm.

A rigidez ao cisalhamento da superfície estreita é D44=15253kN/m comparada a D44=5970,8kN/m da superfície mais larga. Como resultado, apesar de uma carga idêntica, a deformação da superfície mais rígida é menor e a carga de cisalhamento é maior.

Rigidezes em superfícies multicamadas com volumes integrados

No futuro, será possível no Add-On Superfícies Multicamadas definir volumes junto com superfícies. Neste tipo também será exportada uma superfície para o RFEM. Visto que a geração das rigidezes e a decomposição dos esforços internos é mais complexa, isso será detalhado separadamente.

Referências

Construção com CLT - Elementos de madeira maciça portantes para parede, laje e cobertura – Série 4, Parte 6, Episódio 1. Serviço de informação sobre madeira, Berlim, 2016
Estruturas de superfície plana: princípios básicos de modelação e cálculo de painéis e placas
Jones, R. M. (s.d.). Mechanics of Composite Materials (2.ª ed.). Taylor & Francis Inc., Filadélfia.
Arnold, M.: Propriedades mecânicas de madeira laminada diagonal (DLT) com relação a lajes de madeira maciça apoiadas em pontos. Tese de doutoramento em preparação. Cátedra de Construções em Madeira e Estruturas de Edifícios, Universidade Técnica de Munique, 2023

Capítulo principal

Teoria

Modelo

585x

23x

Modelos multicamadas

70x

rigidez de corte