Výchozí metodou integrace v programu RFEM je Gaussova-Lobattova kvadratura s devíti integračními body. Toto standardní nastavení je pro většinu případů dostačující. Pro dostatečně přesné zobrazení nelineárních diagramů napětí-přetvoření (např. u drátkobetonu) může být užitečné zvýšit počet integračních bodů. Při použití nelineárního materiálu je tak možné upravit počet integračních bodů v každé vrstvě mezi 3 a 99 body (viz obrázek Úprava integračních bodů pro vrstvy ). Je však třeba si uvědomit, že vyšší počet integračních bodů vede k delší době výpočtu.
Kromě toho jsou k dispozici tři různé metody integrace (viz obrázek Zadání metody integrace ):
- Gaussova-Lobattova kvadratura
- Simpsonovo pravidlo
- Lichoběžníkové pravidlo
Tyto integrační metody, známé také jako kvadraturní vzorce, jsou vysvětleny níže. Obecně lze předpokládat, že Gaussova-Lobattova kvadratura s pevným počtem integračních bodů poskytuje nejvyšší přesnost, aniž by se výrazně zvýšila výpočetní náročnost. Lichoběžníkové nebo Simpsonovo' pravidlo vede k lepšímu výsledku pouze ve zvláštních případech.
Kvadraturní vzorce
Cílem kvadraturního vzorce je vypočítat numerickou aproximaci k integrálu. Za tímto účelem se vyberou podporové body v oblasti integrace a v těchto bodech se sečtou vážená vyhodnocení funkcí. Výpočet momentu použijeme jako příklad pro následující vysvětlení.
d = výška libovolné vrstvy ve vícevrstvé ploše. Program se pak pokusí integrál aproximovat následovně:
K tomu n bodů rastru −d/2 ≤ z1 < z2 < . . . < zn ≤ d/2 po výšce vrstvy a skalární tíhy ω1, . . . , ωn, které jsou specifické pro příslušný kvadraturní vzorec.
V programu RFEM se vždy používá liché číslo n = 2k + 1 bodů rastru a jako integrační body se vybere alespoň horní, střední a dolní část vrstvy. Z1 = −d/2, zk = 0 a zn = d/2. To je nezbytné, aby bylo možné přesně vypočítat hodnoty napětí v těchto místech a následně je zobrazit v programu. Pokud zadáte sudý počet bodů rastru, použije se pro výpočet další nejvyšší liché číslo.
Míra přesnosti kvadraturní rovnice se udává v jejím řádu p. Jedná se o nejvyšší stupeň polynomu, který je přesně integrován.
Lichoběžníkové pravidlo
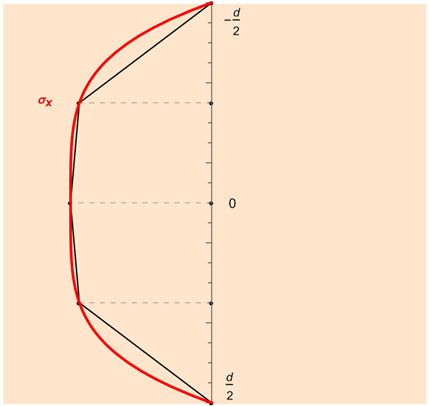
Jednoduchým příkladem kvadraturní rovnice je lichoběžníkové pravidlo. V tomto případě se jako místa podpory zvolí oba vnější okraje oblasti integrace; tedy z1 = −d/2 a z2 = d/2. Lichoběžníkové pravidlo je prvního řádu, protože lineární funkce jsou integrovány přesně, ale kvadratické funkce ne.
V případě varianty kumulativního lichoběžníkového pravidla použité v programu RFEM se při výběru n integračních bodů rozdělí integrační interval ekvidistantně na n − 1 dílčích intervalů a pro každý z nich se použije lichoběžníkové pravidlo.
Na následujícím obrázku je znázorněn příklad sečteného lichoběžníkového pravidla pro pět integračních bodů.
Simpsonovo pravidlo
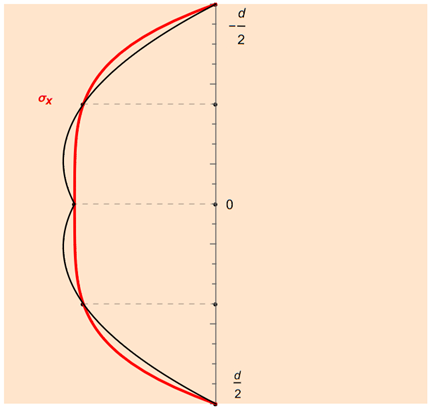
Simpsonovo pravidlo je kvadraturní vzorec třetího řádu, který používá tři integrační body - dva na okrajích a jeden ve středu oblasti integrace. Tíhy se volí tak, aby přibližné řešení odpovídalo integrálu přes parabolu, která prochází těmito třemi body. Pokud z1 = −d/2, z2 = 0 a z3 = d/2, dostaneme tvar:
RFEM zde také používá složenou kvadraturu. Pokud je podporových bodů lichý počet n , dostaneme (n − 1)/2 stejně dlouhé dílčí intervaly, pro které platí Simpsonovo' pravidlo. Obrázek to opět ukazuje jako příklad pro pět integračních bodů.
Gaussova-Lobattova kvadratura
V Gaussově-Lobattově kvadratuře se vždy zadávají oba hraniční body z1 = −d/2 a zn = d/2 jako opěrná místa a všechny ostatní integrační body se vybírají tak, aby bylo dosaženo co nejvyššího řádu. To je p = 2n − 3. Pro n = 3 je Gaussova-Lobattova kvadratura ekvivalentní Simpsonovu' pravidlu; pro n = 5, například: