675x

2020-12-07

VE0019 | Flexão plástica – Carga de momento

Descrição

Uma viga em consola está completamente fixada na extremidade esquerda e carregada por um momento fletor de acordo com o esboço seguinte. O problema é descrito pelo seguinte conjunto de parâmetros. São consideradas pequenas deformações e o peso próprio não é considerado neste exemplo. Determinar a flecha máxima u_z,máx.

Material	Elástico-plástico	Módulo de elasticidade	E	210 000,000	MPa
		coeficiente de Poisson	ν	0,000	-
		Módulo de corte	G	10 5000,000	MPa
		Resistência plástica	f_y	240,000	MPa
Geometria	Viga em consola	perímetro	L	2,000	m
		Largura	al	0,005	m
		Espessura	T	0,005	m
Carga,		Momento fletor	M	6,000	Nm

@sketch@

Flexão plástica – Carga de momento

Solução analítica

A consola é carregada por um momento fletor M. As quantidades desta carga são inicialmente discutidas. O momento M_e para a primeira cedência e o momento último M_p para a estrutura tornar-se uma articulação plástica são calculados da seguinte forma:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Momento elástico

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Momento plástico

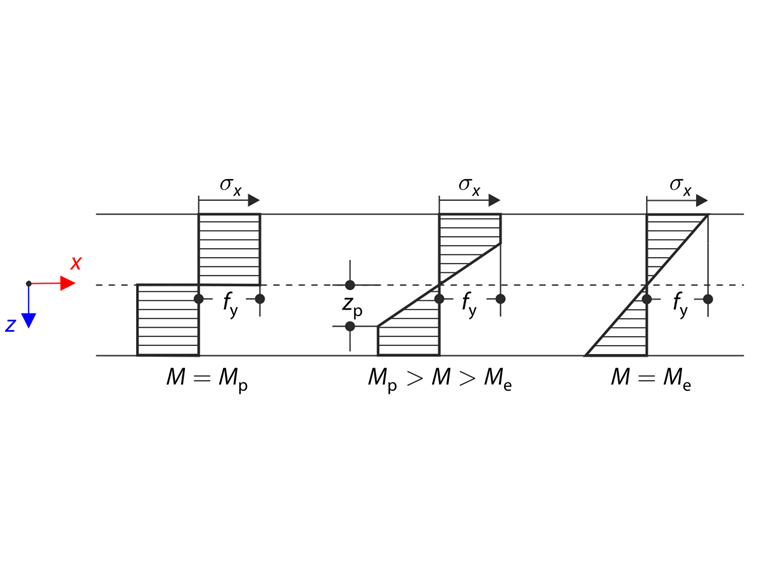
O momento fletor M causa o estado elástico-plástico. A secção no estado elástico-plástico divide-se num núcleo elástico e numa superfície plástica que é descrita pelo parâmetro_z de acordo com o diagrama seguinte.
@schema@

Distribuição de tensões de flexão

z_{p} = \frac{f_{y}}{κ (x) E}

Parâmetro z_p

O momento elástico-plástico M_ep na secção tem de ser igual ao momento fletor M. A curvatura κ resulta desta equação.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

Curvatura,

A flecha total da estrutura u_z,máx é calculada através da integral de Mohr's.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x = κ \frac{L^{2}}{2} = 1.180 m

Deformação total de consola – carga de momento

Configuração do RFEM

Modelado no RFEM 5.16 e no RRFEM 6.01
O tamanho do elemento é l_FE = 0,020 m
A análise geometricamente linear é considerada
O número de incrementos é 5
A rigidez ao corte das barras é desprezada

Resultados

Modelo de material	Solução analítica	RFEM 5		RFEM 6
Modelo de material	u_z,máx [m]	u_z,máx [m]	Relação [-]	u_z,máx [m]	Relação [-]
Ortotrópico plástico 2D	1,180	1.190	1,008	1.190	1,008
Isotrópico plástico 2D/3D, placa		1,173	0,994	1,173	0,994
Isotrópico plástico 1D		1180	1,000	1180	1,000
Isotrópico elástico não linear 2D/3D, placa, Mises		1.190	1,008	1.190	1,008
Isotrópico elástico não linear 2D/3D, placa, Tresca		1.190	1,008	1.190	1,008
Isotrópico plástico 1D		1180	1,000	1180	1,000

493x

Exemplo de verificação 0019 | 1 | Laje | Ortotrópico plástico 2D | Tsai Wu

Referências

Lubliner, J. (1990). Teoria da plasticidade. Nova Iorque: MacMillan.

;