670x

2020-12-07

VE0019 | Flessione plastica - Carico del momento

Descrizione

Uno sbalzo è completamente fissato all'estremità sinistra e caricato da un momento flettente secondo il seguente schizzo. Il problema è descritto dal seguente set di parametri. In questo esempio, vengono considerate piccole deformazioni e il peso proprio è trascurato. Determina la freccia massima u_z,max.

Materiale	Elastico-plastico	Modulo di elasticità	E	210000.000	MPa
		coefficiente di Poisson	ν	0.000	-
		Modulo di taglio	G	105000.000	MPa
		Resistenza plastica	f_y	240.000	MPa
Geometria	Sbalzo	Durata	L	2.000	m
		Larghezza	w	0.005	m
		spessore	t	0.005	m
Carico		Momento flettente	M	6.000	Nm

@sketch@

Flessione plastica - Carico del momento

Soluzione analitica

Lo sbalzo è caricato dal momento flettente M. Le quantità di questo carico sono discusse all'inizio. Il momento M_e quando si verifica il primo snervamento e il momento ultimo M_p quando la struttura diventa cerniera plastica sono calcolati come segue:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Momento elastico

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Momento plastico

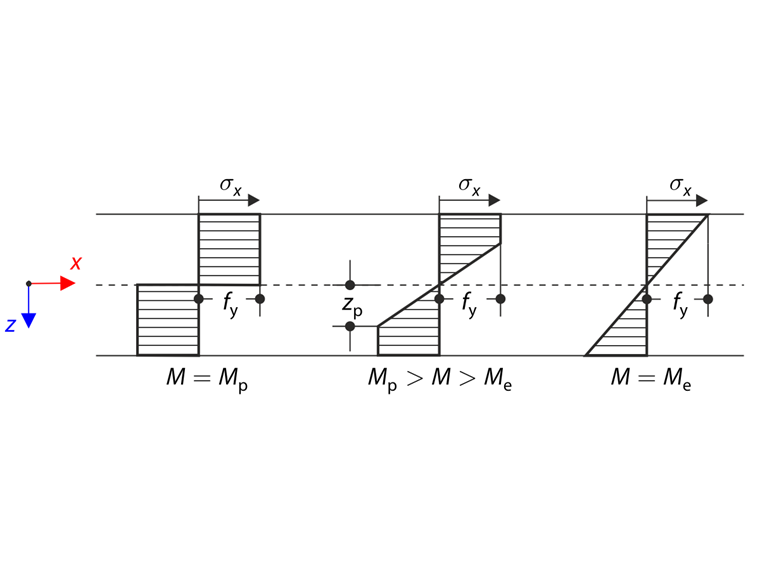
Il momento flettente M determina lo stato elastico-plastico. La sezione trasversale nello stato elastico-plastico è divisa nel nucleo elastico e nella superficie plastica, che è descritta dal parametro z_p secondo il diagramma seguente.
@schema@

Distribuzione della tensione di flessione

z_{p} = \frac{f_{y}}{κ (x) E}

Parametro z_p

Il momento elastico-plastico M_ep nella sezione trasversale deve essere uguale al momento flettente M. La curvatura κ risulta da questa uguaglianza.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

curvatura

L'inflessione totale della struttura u_z,max è calcolata utilizzando l'integrale di Mohr's.

\begin{equation} u_{z,\text{max}}=\int_{0}^{L}\kappa (L-x)\,\text{d}x=\kappa \,\frac{L^{2}}{2}=1.180\,\text{m} \end{equation}

Inflessione totale di console - Carico del momento

Impostazioni di RFEM

Modellato in RFEM 5.16 e RRFEM 6.01
La dimensione dell'elemento è l_FE = 0,020 m
Viene considerata l'analisi geometricamente lineare
Il numero di incrementi è 5
La rigidezza a taglio delle aste è trascurata

Risultati

Modello di materiale	Soluzione analitica	RFEM 5		RFEM 6
Modello di materiale	u_z,max [m]	u_z,max [m]	Rapporto [-]	u_z,max [m]	Rapporto [-]
Plastica ortotropa 2D	1,180	1.190	1.008	1.190	1.008
Isotropo plastico 2D/3D, piastra		1.173	0,994	1.173	0,994
Plastico isotropo 1D		1.180	1.000	1.180	1.000
Isotropo elastico non lineare 2D/3D, piastra, Mises		1.190	1.008	1.190	1.008
Isotropo elastico non lineare 2D/3D, piastra, Tresca		1.190	1.008	1.190	1.008
Plastico isotropo 1D		1.180	1.000	1.180	1.000

491x

Esempio di verifica 0019 | 1 | Parete | Plastica ortotropa 2D | Tsai-Wu

Bibliografia

Lublino, J. (1990). Teoria della plasticità. New York: Macmillan.

;