670x

07.12.2020

VE0019 | Flexion plastique - Charge de moment

Description du projet

Un porte-à-faux est entièrement encastré à l'extrémité gauche et chargé par un moment fléchissant selon le schéma suivant. Le problème est décrit par les ensembles de paramètres suivants. Les petites déformations sont considérées et le poids propre est négligé dans cet exemple. Déterminer la flèche maximale u_z,max.

Matériau	Élastique-plastique	Module d'élasticité	E	210000,000	MEP
		coefficient de Poisson	P	0,000
		Module de cisaillement	G	105000,000	MEP
		Résistance plastique	_fy	240 000	MEP
Géométrie	Porte-à-faux	Périmètre	L	2 000	m
		Largeur	w	0,005	m
		Épaisseur	t	0,005	m
Import		Moment fléchissant	M	6 000	Nm

@sketch@

Flexion plastique - Charge de moment

Solution analytique

Le porte-à-faux est chargé par le moment fléchissant M. Les grandeurs de cette charge sont tout d'abord abordées. Le moment M_e lorsque la première plastification se produit et le moment ultime M_p lorsque la structure devient une articulation plastique :

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Moment élastique

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Moment plastique

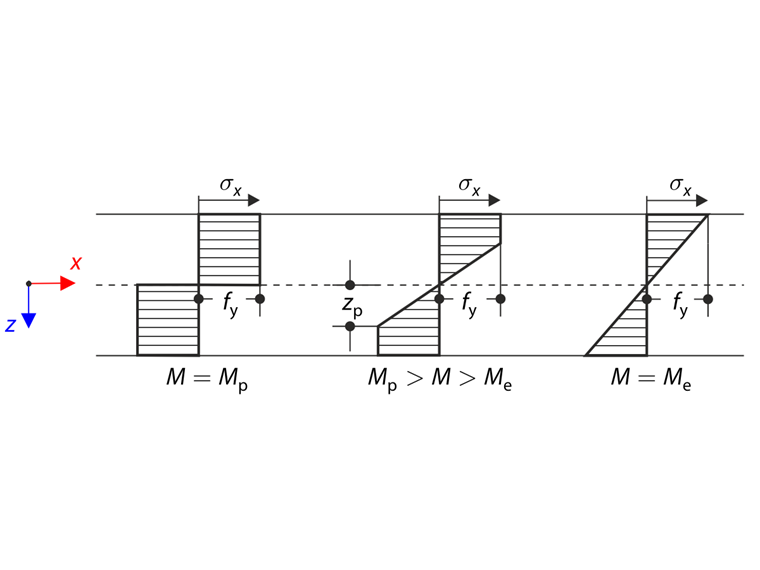
Le moment fléchissant M est à l'origine de l'état élastique-plastique. La section à l'état élastique-plastique est divisée en noyau élastique et surface plastique, qui est décrite par le paramètre z_p selon le diagramme suivant.
@schema@

Distribution des contraintes de flexion

z_{p} = \frac{f_{y}}{κ (x) E}

Paramètre z_p

Le moment plastique élastique M_ep dans la section doit être égal au moment fléchissant M. La courbure κ résulte de cette égalité.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

Flèche

La flèche totale de la structure u_z,max est calculée à l'aide de l'intégrale de Mohr's.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x = κ \frac{L^{2}}{2} = 1.180 m

Flèche totale du porte-à-faux charge de moment

Paramètres RFEM

Modélisé dans RFEM 5.16 et RRFEM 6.01
La taille de l'élément est l_EF = 0,020 m
L'analyse géométriquement linéaire est considérée
Le nombre d'incréments est de 5
La rigidité de cisaillement des barres est négligée

Résultats

Modèle de matériau	Solution analytique	RFEM5		RFEM 6
Modèle de matériau	_uz,max [m]	_uz,max [m]	Rapport [-]	_uz,max [m]	Rapport [-]
Orthotrope plastique 2D	1,180	1,190	1,008	1,190	1,008
Isotrope plastique 2D/3D, plaque	1,173	0,994	1,173	0,994
Isotrope plastique 1D	1,180	1 000	1,180	1 000
Isotrope non linéaire élastique 2D/3D, plaque, Mises	1,190	1,008	1,190	1,008
Isotrope non linéaire élastique 2D/3D, Plaque, Tresca	1,190	1,008	1,190	1,008
Isotrope plastique 1D	1,180	1 000	1,180	1 000

493x

Exemple de vérification 0019 | 1 | Plaque | Orthotrope plastique 2D | Tsai-Wu

Références

Licence, J. (1990). Théorie de la plasticité. New York : Macmillan, 1993

;