402x

2020-12-07

VE0019 | 塑性弯曲 – 弯矩荷载

项目介绍

如下图所示，设置一个悬臂梁，其左端完全固定，并施加弯矩。 The problem is described by the following set of parameters. Small deformations are considered and the self-weight is neglected in this example. Determine the maximum deflection u_z,max.

Material	Elastic-Plastic	弹性模量	E	210000.000	MPa
		泊松比	ν	0.000	-
		剪切模量	G	105000.000	MPa
		Plastic Strength	f_y	240.000	MPa
Geometry	Cantilever	周长	L	2.000	m
		宽度	w	0.005	m
		厚度	t	0.005	m
Load		弯矩	M	6.000	Nm

塑性弯曲 – 弯矩荷载

Analytical Solution

The cantilever is loaded by the bending moment M. The quantities of this load are discussed at first. The moment M_e when the first yield occurs and the ultimate moment M_p when the structure becomes plastic hinge are calculated as follows:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

弹性弯矩

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

塑性弯矩

The bending moment M causes the elastic-plastic state. The cross-section in the elastic-plastic state is divided into the elastic core and the plastic surface, which is described by the parameter z_p according to the following diagram.

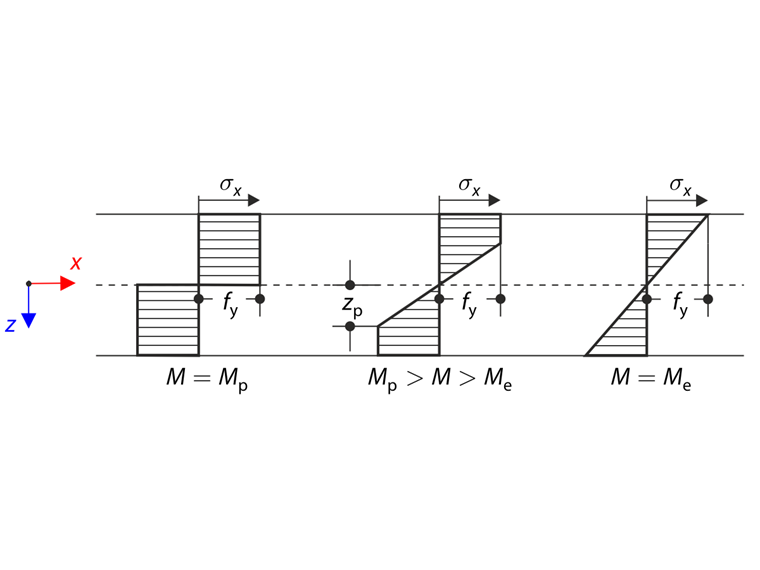
弯曲应力分布

z_{p} = \frac{f_{y}}{κ (x) E}

参数 z_p

The elastic-plastic moment M_ep in the cross-section has to equal to the bending moment M. The curvature κ results from this equality.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

曲率

The total deflection of the structure u_z,max is calculated using the Mohr's integral.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x

悬臂梁的总挠度

RFEM Settings

Modeled in RFEM 5.16 and RRFEM 6.01
The element size is l_FE= 0.020 m
Geometrically linear analysis is considered
The number of increments is 5
Shear stiffness of the members is neglected

结果

Material Model	Analytical Solution	RFEM 5		RFEM 6
Material Model	u_z,max [m]	u_z,max [m]	Ratio [-]	u_z,max [m]	Ratio [-]
Orthotropic Plastic 2D	1.180	1.190	1.008	1.190	1.008
Isotropic Plastic 2D/3D, Plate		1.173	0.994	1.173	0.994
一维各向同性塑性		1.180	1.000	1.180	1.000
Isotropic Nonlinear Elastic 2D/3D, Plate, Mises		1.190	1.008	1.190	1.008
Isotropic Nonlinear Elastic 2D/3D, Plate, Tresca		1.190	1.008	1.190	1.008
一维各向同性塑性		1.180	1.000	1.180	1.000

428x

验算示例 0019 | 1 | 墙板 | 二维正交各向异性塑性 | 才武

参考

Lubliner, J. (1990)。 塑性理论。纽约： Macmillan 公司。

;