670x

7.12.2020

VE0019 | Plastický ohyb - momentové zatížení

Popis

Konzola je plně fixována na levém konci a zatížena ohybovým momentem podle následujícího náčrtu. Problém je popsán pomocí následující sady parametrů. V tomto příkladu se zohlední malé deformace a vlastní tíha se zanedbá. Stanovíme maximální průhyb u_z,max.

Materiál	Pružný-plastický	Modul pružnosti	E	210000,000	MPa
		Poissonův součinitel	ν	0,000	-
		Smykový modul	G	105000,000	MPa
		Plastická pevnost	f_y	240,000	MPa
Geometrie	Konzola	obvod	L	2,000	m
		Šířka	w	0,005	m
		Tloušťka	t	0,005	m
Zatížení		Ohybový moment	M	6,000	Nm

@sketch@

Plastický ohyb - momentové zatížení

Analytické řešení

Konzola je zatížena ohybovým momentem M. Nejdříve se budeme zabývat velikostmi tohoto zatížení. Moment_Me při prvním tečení a mezní moment M_p, kdy se konstrukce stává plastickým kloubem, se počítají následovně:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Pružný moment

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Plastický moment

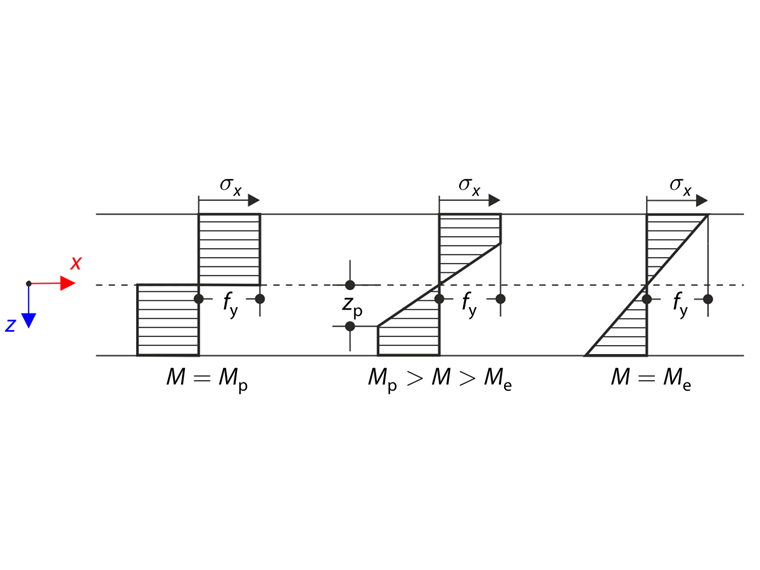
Ohybový moment M způsobuje pružno-plastický stav. Průřez v pružno-plastickém stavu se dělí na pružné jádro a plastickou plochu, která je popsána parametrem z_p podle následujícího diagramu.
@schema@

Průběh napětí v ohybu

z_{p} = \frac{f_{y}}{κ (x) E}

Parametr z_p

Pružno-plastický moment_Mep v průřezu se musí rovnat ohybovému momentu M. Z této rovnosti vyplývá zakřivení κ.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

Zakřivení

Celkový průhyb konstrukce u_z,max se vypočítá pomocí Mohrova' integrálu.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x = κ \frac{L^{2}}{2} = 1.180 m

Celkový průhyb konzoly - Zatížení momentem

Nastavení programu RFEM

Modelováno v programech RFEM 5.16 a RRFEM 6.01
Velikost prvku je l_FE = 0,020 m
Uvažuje se geometricky lineární analýza
Počet přírůstků je 5
Smyková tuhost prutů se zanedbává

Výsledky

Materiálový model	Analytické řešení	RFEM 5		RFEM 6
Materiálový model	u_z,max [m]	u_z,max [m]	Poměr [-]	u_z,max [m]	Poměr [-]
Ortotropní plastický 2D	1,180	1,190	1,008	1,190	1,008
Izotropní plastický 2D/3D, deska		1,173	0,994	1,173	0,994
Izotropní plastický 1D		1,180	1,000	1,180	1,000
Izotropní nelineární elastický 2D/3D, deska, Mises		1,190	1,008	1,190	1,008
Izotropní nelineární elastický 2D/3D, deska, Tresca		1,190	1,008	1,190	1,008
Izotropní plastický 1D		1,180	1,000	1,180	1,000

491x

Verifikační příklad 0019 | 1 | Plocha | Ortotropní plastický 2D | Tsai-Wu

Reference

Lubliner, J. (1990). Teorie plasticity. New York: Macmillan.

;