675x

2020-12-07

VE0019 | Пластический изгиб – моментная нагрузка

Описание работы

Консоль полностью защемлена на левом конце и загружена изгибающим моментом согласно следующему эскизу. Данная проблема описывается следующим набором параметров. В данном примере учитываются небольшие деформации, а собственный вес не учитывается. Задать максимальный прогиб u_z,max.

Материал	Упруго-пластическая	Модуль упругости	E	210000.000	МПа
		коэффициент Пуассона	ν	0,000	-
		Модуль сдвига	G	105000.000	МПа
		Пластическая прочность	_fy	240,000	МПа
Геометрия	консоль	Длительность	L	2,000	м
		Ширина	W	0,005	м
		толщина	t	0,005	м
Нагрузки		изгибающий момент	M	6,000	Нм

@sketch@

Пластический изгиб – моментная нагрузка

Аналитическое решение

На консоль действует изгибающий момент М. Сначала обсуждаются величины данной нагрузки. Момент M_e при достижении первого предела текучести и предельный момент M_p, когда конструкция становится пластическим шарниром, рассчитываются следующим образом:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Упругий момент

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Пластический момент

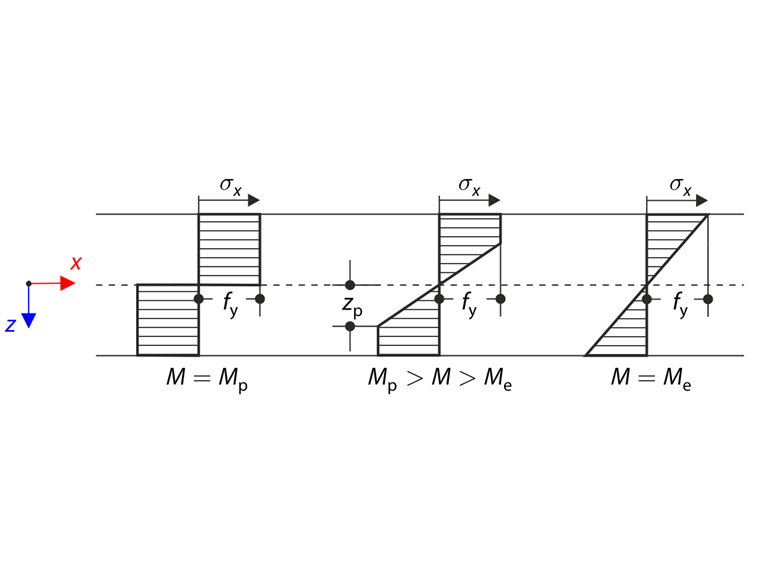
Изгибающий момент M вызывает упруго-пластическое состояние, Сечение в упруго-пластическом состоянии разделяется на упругое ядро и пластическую поверхность, которая описывается параметром z_p по следующей диаграмме.
@schema@

Распределение изгибающих напряжений

z_{p} = \frac{f_{y}}{κ (x) E}

Параметр z_p

Упругопластический момент M_ep в сечении должен быть равен изгибающему моменту M. Кривизна κ затем определяется данным равенством.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

Кривизна

Общий прогиб конструкции u_z,max рассчитывается с помощью интеграла Мора.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x = κ \frac{L^{2}}{2} = 1.180 м

Суммарый прогиб консоли - нагрузка моментом

Параметры RFEM

Смоделировано в программе RFEM 5.16 и RRFEM 6.01
Размер элемента равен l_FE = 0,020 м
Учитывается геометрически линейный расчёт
Количество приращений - 5
Жесткостью на сдвиг стержней не учитывается

Результаты

Модель материала	Аналитическое решение	RFEM 5		Rfem 6
Модель материала	u_z,max [м]	u_z,max [м]	Соотношение [-]	u_z,max [м]	Соотношение [-]
Ортотропная пластическая 2D	1,180	1,190	1,008	1,190	1,008
Изотропная пластическая 2D/3D, плита	1,173	0,994	1,173	0,994
Изотропная пластичная 1D	1,180	1,000	1,180	1,000
Изотропная нелинейная упругая 2D/3D, плита, Мизес	1,190	1,008	1,190	1,008
Изотропная нелинейная упругая 2D/3D, плита, по Треске	1,190	1,008	1,190	1,008
Изотропная пластичная 1D	1,180	1,000	1,180	1,000

493x

Контрольный пример 0019 | 1 | Пластина | Ортотропная пластическая 2D | Цай-Ву

Ссылки

Люблинер, J .: (1990). Теория пластичности. Нью-Йорк: MacMillen, 2015

;