675x

2020-12-07

VE0019 | Zginanie plastyczne – obciążenie momentem

Opis prac

Wspornik jest w pełni zamocowany na lewym końcu i obciążony momentem zginającym zgodnie z poniższym szkicem. Problem opisano za pomocą poniższego zestawu parametrów. W tym przykładzie uwzględniane są niewielkie odkształcenia, a ciężar własny jest pomijany. Określ maksymalne ugięcie u_z,max.

Materiał	Sprężysto-plastyczny	Moduł sprężystości	E	210000.000	MPa
		współczynnik Poissona	ν	0.000	-
		Moduł ścinania	G	105000.000	MPa
		Wytrzymałość plastyczna	f_y	240.000	MPa
Geometria	Wspornik	obwiednia	L	2.000	m
		Szerokość	w	0,005	m
		Grubość	t	0,005	m
Obciążenie		moment zginający	M	6000	Nm

@sketch@

Zginanie plastyczne – obciążenie momentem

Rozwiązanie analityczne

Wspornik jest obciążony momentem zginającym M. Najpierw omówiono wielkości tego obciążenia. Moment M_e występujący w chwili wystąpienia pierwszej plastyczności oraz moment graniczny sprężystości M_p w chwili, gdy konstrukcja staje się przegubem plastycznym są obliczane w następujący sposób:

M_{e} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} \frac{2 f_{y}}{t} z^{2} w d z = \frac{f_{y} w t^{2}}{6}

Moment sprężysty

M_{p} = 2 \int_{0}^{t / 2} σ (z) z w d z = 2 \int_{0}^{t / 2} f_{y} z w d z = \frac{f_{y} w t^{2}}{4}

Moment plastyczny

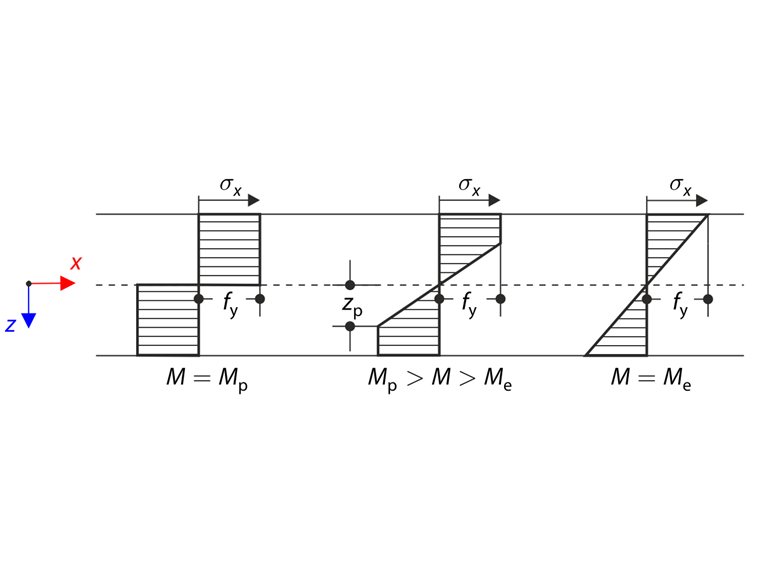
Moment zginający M wywołuje stan sprężysto-plastyczny. Przekrój w stanie sprężysto-plastycznym jest podzielony na rdzeń sprężysty i powierzchnię plastyczną, która jest opisana parametrem z_p zgodnie z poniższym wykresem.
@schema@

Rozkład naprężeń zginających

z_{p} = \frac{f_{y}}{κ (x) E}

Parametr z_p

Moment sprężysto-plastyczny M_ep w przekroju musi być równy momentowi zginającym M. Krzywizna κ wynika z tej równości.

κ = \frac{f_{y}}{E} \sqrt{\frac{1}{3 (\frac{t^{2}}{4} - \frac{M}{f_{y} w})}}

krzywizna

Całkowite ugięcie konstrukcji u_z,max jest obliczane przy użyciu całki Mohra'.

u_{z, \max} = \int_{0}^{L} κ (L - x) d x = κ \frac{L^{2}}{2} = 1.180 m

Całkowite ugięcie wspornika - obciążenie momentem

Ustawienia RFEM

Modelowany w RFEM 5.16 i RRFEM 6.01
Rozmiar elementu wynosi l_FE = 0.020 m
Uwzględniana jest analiza geometrycznie liniowa
Liczba przyrostów wynosi 5
Sztywność prętów na ścinanie jest pominięta

Wyniki

Model materiałowy	Rozwiązanie analityczne	RFEM 5		RFEM 6
Model materiałowy	u_z,max [m]	u_z,max [m]	Stosunek [-]	u_z,max [m]	Stosunek [-]
Ortotropowy plastyczny 2D	1,180	1,190	1.008	1,190	1.008
Izotropowy plastyczny 2D/3D, płytowy		1,173	0.994	1,173	0.994
Izotropowy Plastyczny 1D		1,180	1,000	1,180	1,000
Izotropowy nieliniowo sprężysty 2D/3D, płytowy, Mises		1,190	1.008	1,190	1.008
Izotropowy nieliniowy sprężysty 2D/3D, płytowy, Tresca		1,190	1.008	1,190	1.008
Izotropowy Plastyczny 1D		1,180	1,000	1,180	1,000

493x

Przykład obliczeniowy 0019 | 1 | Płyta | Ortotropowa plastyka 2D | Tsai-Wu

Odniesienia

Lubliner, J. (1990). Teoria plastyczności. Nowy Jork: Macmillana.

;