15819x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

2018-06-27

Законы ортотропных материалов

Законы ортотропных материалов применяются в каждом случае, в котором материалы расположены в соответствии с их загружением. Примером являются армированные волокном пластмассы, профилированный лист, железобетон или древесина.

Закон Гука обычно учитывается для ортотропных материалов

u = \frac{E}{2 G} - 1 \leq 0.5

Формула 1

т.е.

- 1 < u < 0.5

Формула 2

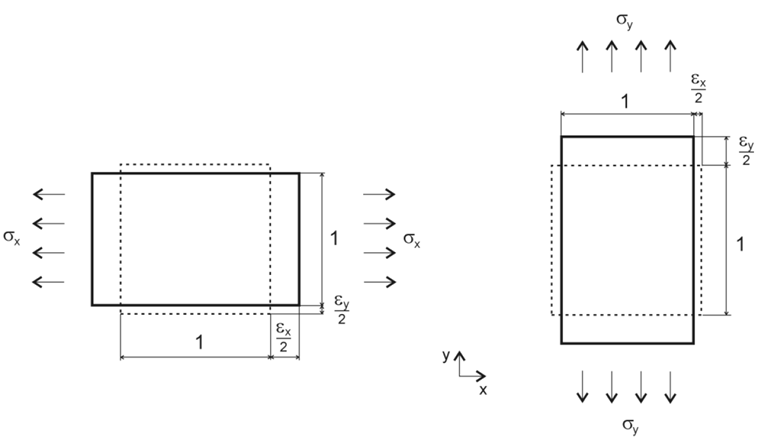
больше не действует.

поперечная деформация

Следующие параметры материала относятся к двумерной жесткости и, если не указано иначе, относятся к деревянному материалу. В качестве основы зададим локальную систему осей, как показано на рисунке 01.

E_x = жесткость в локальном направлении поверхности x
Ey = жесткость в локальном направлении поверхности y
G_xz = жесткость на сдвиг в локальном направлении поверхности x (направление толщины плиты)
G_yz = жесткость на сдвиг в локальном направлении поверхности y (направление толщины плиты)
G_xy = жесткость на сдвиг в плоскости плиты
ν_xy = поперечная деформация в направлении x
ν_yx = поперечная деформация в направлении y

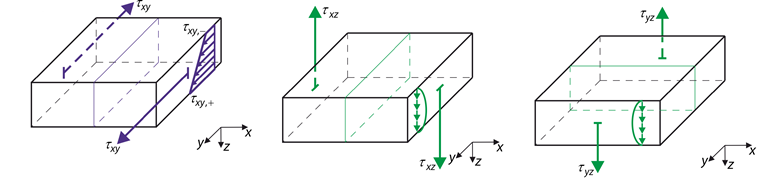
Напряжения, показанные на рисунке 02, связаны с выше упомянутыми жесткостями.

Касательные напряжения

Свойства материала подчиняются следующим правилам.

Уравнение 1:

\frac{u_{yx}}{E_{y}} = \frac{u_{xy}}{E_{x}}

Формула 3

Уравнение 2:

u_{xy} ⩾ u_{yx}

Формула 4

Уравнение 3:

u_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot u_{yx}

Формула 5

Уравнение 4:

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Формула 6

Соотношение деформаций в упомянутых выше уравнениях подчеркивает соотношения, показанные на рисунке 01.

Жесткость в плоскостной области рассчитывается следующим образом.

Уравнение 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Формула 7

Поперечная деформация ν

На рисунке 01 мы видим, что изменение деформаций и напряжений в данном направлении является результатом более однородных свойств материала в соответствующем направлении.

Соотношение деформаций:

Уравнение 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Формула 8

Уравнение 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Формула 9

Простой вопрос - быстрый ответ:

σ_{x} e q 0, σ_{y} = 0, σ_{xy} = 0

Формула 10

по закону Гука мы получим следующие уравнения.

Уравнение 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Формула 11

Уравнение 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Формула 12

Уравнение 10:

σ_{y} = ε_{y} \cdot E_{y} with E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Формула 13

Уравнение 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Формула 14

Уравнение 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} with ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Формула 15

Уравнение 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Формула 16

Матрица жесткости

Расчет глобальной матрицы жесткости плиты.

Уравнение 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Формула 17

Изгибные компоненты:

Уравнение 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Формула 18

Уравнение 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Формула 19

Уравнение 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Формула 20

Уравнение 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Формула 21

Мембранные компоненты:

Уравнение 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - u_{xy} u_{yx}}

Формула 22

Уравнение 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Формула 23

Уравнение 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - u_{xy} u_{yx}}

Формула 24

Уравнение 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Формула 25

Компоненты среза:

Уравнение 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Формула 26

Уравнение 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Формула 27

Предпосылкой этих уравнений является то, что матрица жесткости положительна, т.е. все собственные значения матрицы положительны.

По этой причине RFEM проверит, кроме прочего, ввод поперечной деформации с помощью следующего уравнения.

Уравнение 25:

u_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Формула 28

Пример

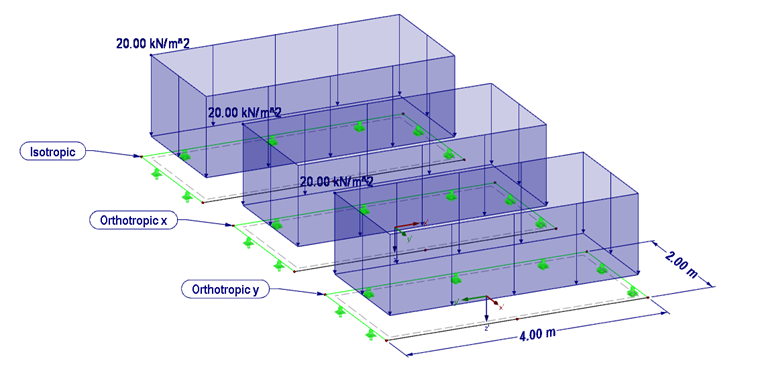
Свойства ортотропного материала мы поясним на следующем примере (рисунок 03). Мы сравним ортотропный материал с изотропным материалом. Кроме того, зададим высокую жесткость ортотропной плиты в направлении x и в направлении y.

Система

Конструкция:

Толщина плиты 200 мм
Материал C 24
Ортотропная жесткость

$\begin{array}{l} E_{x} = 1, 100.0 кН / {см}^{2} \\ E_{y} = 37.0 кН / {см}^{2} \\ G_{y} = 6.9 кН / {см}^{2} \\ G_{x} = 69.0 кН / {см}^{2} \\ G_{xy} = 69.0 кН / {см}^{2} \\ u_{xy} = 2.52 \\ u_{yx} = 0.085 \end{array}$

Формула 29
Изотропная жесткость

$\begin{array}{l} E = 1, 100 кН / {см}^{2} \\ G = 500 кН / {см}^{2} \\ u = 0.1 \end{array}$

Формула 30
Размер w = 2,0 м, l = 4,0 м
Нагрузка 20 кН/м²
Размер сетки КЭ 50 см

Конструкция, благодаря опиранию, жестко защемлена в вертикальном направлении z. Условия опирания в направлениях х и у были выбраны таким образом, чтобы не возникало воздействий от защемления.

Расчет выполняется по статическому линейному анализу с учетом линейно-упругих свойств материала и условий опирания.

По закону Гука с заданными значениями мы получим следующую поперечную деформацию.

Уравнение 26:

ν = (\sqrt{E_{x} \cdot E_{y}}) / (2 G) - 1 = 6.97

Формула 31

Так высокая поперечная деформация невозможна для выбранной модели материала. Однако с помощью уравнений из нормы [1], значения можно скорректировать.

Уравнение 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Формула 32

Уравнение 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Формула 33

Уравнение 29:

ν_{xy} = (\frac{\sqrt{1, 100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1, 100}{37}} = 2.52

Формула 34

Уравнение 30:

ν_{xy} = (\frac{\sqrt{1, 100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1, 100}} = 0.085

Формула 35

Поверхности и их жесткость

Результаты:
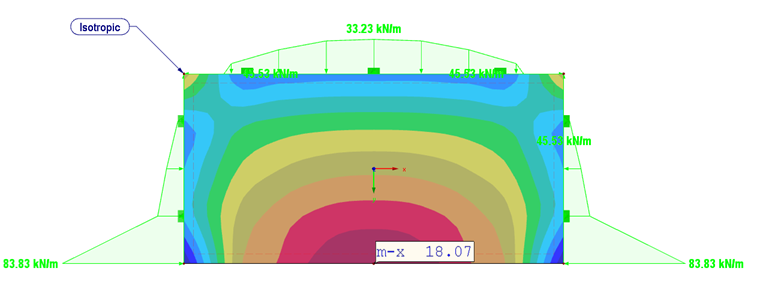
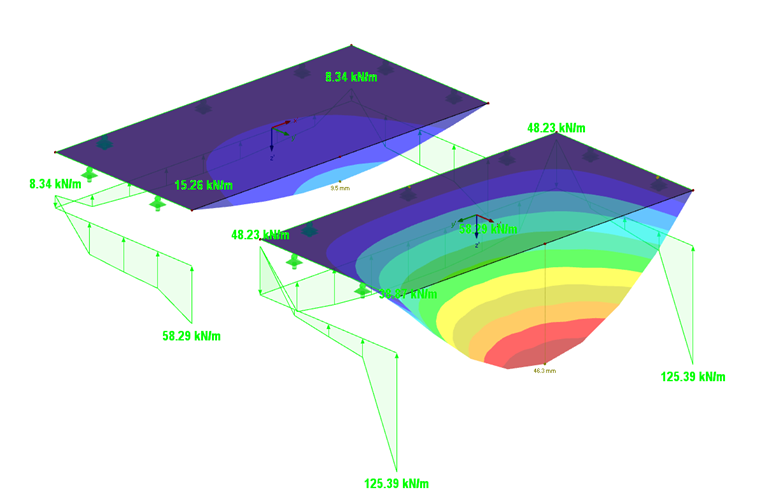
Как и ожидалось, наибольшие деформации происходят при направленности жесткости в направлении y (рисунок 06). Опорная реакция и момент изотропной плиты показаны на рисунке 05.

Результаты изотропного материала

Так как плита с высокой жесткостью в направлении y (E_y = 1100 кН/см²) обладает высокой прочностью в данном направлении, в нем наблюдаются и более высокие опорные реакции (125,4 кНм по сравнению с 58,3 кНм).

Деформации и опорные реакции ортотропных плит

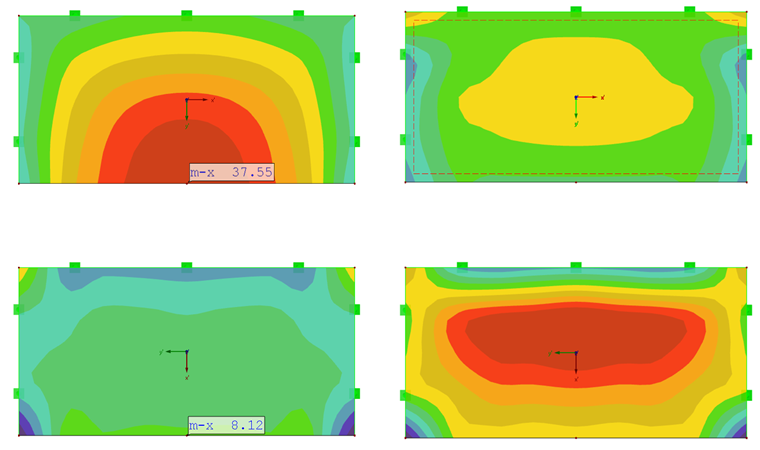
Полученные максимальные изгибающие моменты ортотропных плит равны m_xдля жесткости в направлении x и m_yдля высокой жесткости в направлении y.

У плиты с высокой жесткостью в направлении y максимальный изгибающий момент m_yнаходится почти в центре плиты (рисунок 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Изменения поперечной деформации

Поперечная деформация, согласно диаграмме деформаций, может достигнуть максимальных и минимальных значений, указанных в таблице, для материала прочности C24.

	макс.	Мин.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

Поэтому плита, заданная в начале с высокой жесткостью (E_x = 11 000), будет задана с данными высокими поперечными деформациями. Другие жесткости плиты не изменятся.

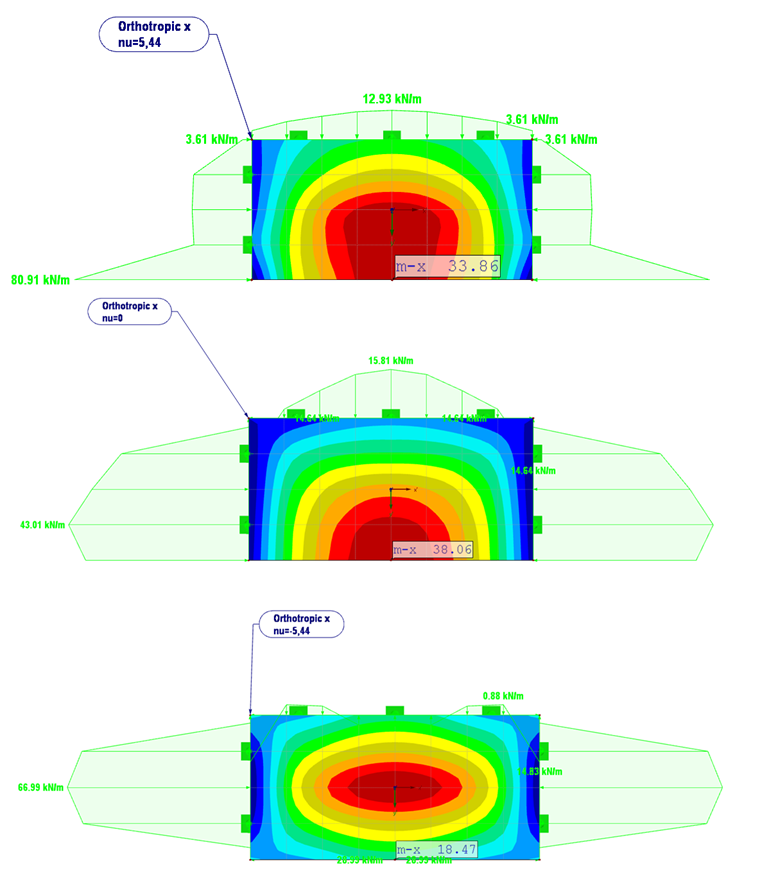
На рисунке 08 показаны результаты изменения ν_xy от 5,44 до -5,44.

При ν_xy = 5,44 опорные реакции качественно соответствуют изотропным свойствам материала. Изгибающий момент увеличивается от m_x = 18,1 кНм/м (изотропная плита) до m_x = 34,9 кНм/м (ортотропная плита)

По сравнению с ортотропной плитой, имеющей обычные поперечные деформации, (ν_xy = 2,5) изгибающий момент немного уменьшается.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, средний: νxy = 0, справа: νxy = -5,44)

При ν_xy = 0 высокая амплитуда опорной реакции на свободном конце плиты распределится в постоянную величину 43 кН/м

Момент m_x возрастет до 38,1 кНм/м. По сравнению с предыдущим результатом (ν_xy =5,44), здесь проявляется воздействие поперечной деформации. При ν = 0, напряжений и искривления из-за поперечной деформации не возникает.

При ν_xy = -5,44 наблюдается надкритический отказ на свободном конце пластины, и опорные реакции будут отрицательными. Максимальный момент наблюдается в центре плиты и равен 59,5 кНм/м.

Плита теперь обладает скорее свойствами одноосно напряженной плиты без третьей опоры в продольном направлении.

Эти свойства можно объяснить с помощью рисунка 01 и приведенных здесь соотношений.

Из-за высокой отрицательной поперечной деформации (ν_xy = -5,44), плита подвергается избыточному сжатию на свободном конце и поэтому не может быть деформирована.

Воздействие ортотропии в направлении y в этом случае почти равно нулю (E_y ≈ 0).

Заключение

С помощью ортотропной модели материала в RFEM можно задать практически любые параметры материала. При изменениях поперечных деформаций можно получить очень различные результаты. После корректировки значений поперечной деформации по норме [1] мы получим значения, близкие к решению для однопролетной балки.

Уравнение 31:

M_{y} = \frac{q l^{2}}{8} = 40 кНм

Формула 36

Слишком высокие отрицательные поперечные деформации указывают на модифицированную конструктивную систему, которая больше не соответствует нашей модели.

Автор

Г-н Кун отвечает за разработку продуктов для деревянных конструкций и оказывает техническую поддержку нашим клиентам.

Ссылки

Программы для нелинейного расчёта

Ссылки

Хубер, М.: T : The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Скачивания

;