15816x

001525

Dipl.-Ing. (FH) Bastian Kuhn, M.Sc.

27. Juni 2018

Orthotrope Materialgesetze

Orthotrope Materialgesetze finden überall dort Verwendung, wo Materialien entsprechend ihrer Beanspruchung angeordnet werden. Beispiele hierfür sind faserverstärkte Kunststoffe, Trapezbleche, bewehrter Beton oder Holz.

Im Regelfall ist bei den orthotropen Materialien das hookesche Gesetz mit

ν = \frac{E}{2 G} - 1 \leq 0, 5

Formel 1

und

- 1 < ν < 0, 5

Formel 2

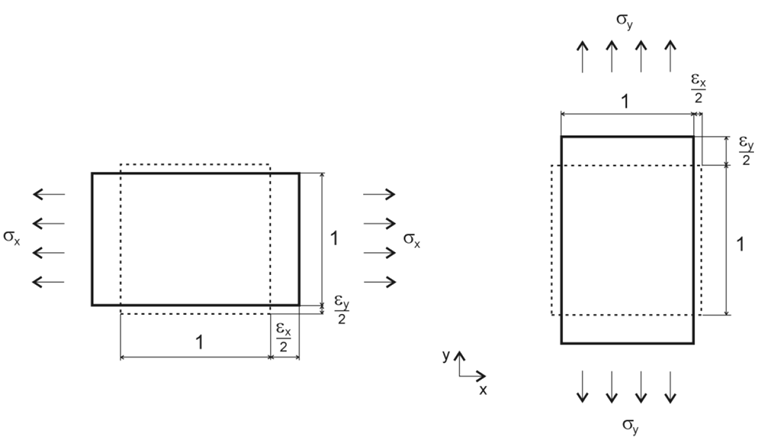
nicht mehr gültig.

Querdehnung

Die folgenden Materialparameter beziehen sich auf zweidimensionale Steifigkeiten und, so weit nicht anders benannt, auf das Material Holz. Es wird ein lokales Achsensystem wie in Bild 01 zugrunde gelegt.

E_x = Steifigkeit in lokaler x-Richtung der Fläche
E_y = Steifigkeit in lokaler y-Richtung der Fläche
G_xz = Schubsteifigkeit in lokaler x-Richtung der Fläche (Dickenrichtung der Platte)
G_yz = Schubsteifigkeit in lokaler y-Richtung der Fläche (Dickenrichtung der Platte)
G_xy = Schubsteifkgeit in Scheibenebene
ν_xy = Querdehnung in x-Richtung
ν_yx = Querdehnung in y-Richtung

Die Spannungen in Bild 02 stehen mit den hier genannten Steifigkeiten in Beziehung.

Schubspannungen

Das Materialgesetz unterliegt folgenden Regeln.

Gleichung 1:

\frac{ν_{yx}}{E_{y}} = \frac{ν_{xy}}{E_{x}}

Formel 3

Gleichung 2:

ν_{xy} \geq ν_{yx}

Formel 4

Gleichung 3:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} = \frac{E_{x}}{E_{y}} \cdot ν_{yx}

Formel 5

Gleichung 4 (Steifigkeiten in Scheibenebene ESZ):

[\begin{matrix} ε_{x} \\ ε_{y} \\ γ_{xy} \end{matrix}] = [\begin{matrix} \frac{1}{E_{x}} & - \frac{ν_{xy}}{E_{x}} & 0 \\ - \frac{ν_{xy}}{E_{x}} & \frac{1}{E_{y}} & 0 \\ 0 & 0 & G_{xy} \end{matrix}] \cdot [\begin{matrix} σ_{x} \\ σ_{y} \\ τ_{xy} \end{matrix}]

Formel 6

Das Verhältnis der Dehnungen in obigen Gleichungen unterstreicht die Beziehungen in Bild 01.

Die Steifigkeiten in Scheibenebene berechnen sich wie folgt.

Gleichung 5:

d_{i} = [\begin{matrix} d_{11, i} & d_{12, i} & 0 \\ d_{22, i} & 0 \\ sym & d_{33, i} \end{matrix}] = [\begin{matrix} \frac{E_{x, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & \frac{ν_{xy, i} E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ \frac{E_{y, i}}{1 - ν_{xy, i}^{2} \frac{E_{y, i}}{E_{x, i}}} & 0 \\ sym & G_{xy, i} \end{matrix}]

Formel 7

Querdehnung ν

Wie bereits in Bild 01 erläutert, resultieren aus dem weicheren Materialverhalten in der jeweiligen Richtung veränderte Verformungen und Spannungen in dieser Richtung.

Verhältnis der Dehnungen:

Gleichung 6:

ν_{xy} = - \frac{ε_{y}}{ε_{x}} \to ε_{y} = - ν_{x} \cdot ε_{x}

Formel 8

Gleichung 7:

ν_{yx} = - \frac{ε_{x}}{ε_{y}} \to ε_{x} = - ν_{y} \cdot ε_{y}

Formel 9

Für

σ_{x} \neq 0, σ_{y} = 0, σ_{xy} = 0

Formel 10

ergeben sich mit dem hookeschen Gesetz folgende Gleichungen.

Gleichung 8:

ε_{x} = \frac{σ_{x}}{E_{x}}

Formel 11

Gleichung 9:

ε_{y} = \frac{σ_{y}}{E_{y}}

Formel 12

Gleichung 10:

σ_{y} = ε_{y} \cdot E_{y} mit E_{y} = \frac{ν_{yx} \cdot E_{x}}{ν_{xy}} \to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot E_{x}}{ν_{xy}}

Formel 13

Gleichung 11:

\to σ_{y} = ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}

Formel 14

Gleichung 12:

\to ε_{y} = \frac{ε_{y} \cdot \frac{ν_{yx} \cdot \frac{σ_{x}}{ε_{x}}}{ν_{xy}}}{E_{y}} mit ν_{xy} = - \frac{ε_{y}}{ε_{x}}

Formel 15

Gleichung 13:

\to ε_{y} = \frac{ε_{y} \cdot ν_{yx} \cdot σ_{x}}{ε_{x} \cdot (- \frac{ε_{y}}{ε_{x}}) \cdot E_{y}} = - \frac{ν_{yx} \cdot σ_{x}}{E_{y}}

Formel 16

Steifigkeitsmatrix

Berechnung der globalen Steifigkeitsmatrix der Platte.

Gleichung 14:

D = [\begin{matrix} D_{11} & D_{12} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{22} & 0 & 0 & 0 & 0 & 0 & 0 \\ D_{33} & 0 & 0 & 0 & 0 & 0 \\ D_{44} & 0 & 0 & 0 & 0 \\ D_{55} & 0 & 0 & 0 \\ sym & D_{66} & 0 & 0 \\ D_{77} & 0 \\ D_{88} \end{matrix}]

Formel 17

Biegeanteile:

Gleichung 15:

D_{11} = \frac{d^{3}}{12} \cdot d_{11} \hat{=} \frac{E_{x} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formel 18

Gleichung 16:

D_{12} = \frac{d^{3}}{12} \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{11} D_{22}}

Formel 19

Gleichung 17:

D_{22} = \frac{d^{3}}{12} \cdot d_{22} \hat{=} \frac{E_{y} d^{3}}{12 (1 - ν_{xy} ν_{yx})}

Formel 20

Gleichung 18:

D_{33} = \frac{d^{3}}{12} \cdot d_{33} \hat{=} G_{xy} \frac{d^{3}}{12}

Formel 21

Scheibenanteile:

Gleichung 19:

D_{66} = d \cdot d_{11} \hat{=} \frac{E_{x} d}{1 - ν_{xy} ν_{yx}}

Formel 22

Gleichung 20:

D_{67} = d \cdot d_{12} \hat{=} sgn (ν_{xy}) \sqrt{ν_{xy} ν_{yx} D_{66} D_{77}}

Formel 23

Gleichung 21:

D_{77} = d \cdot d_{22} \hat{=} \frac{E_{y} d}{1 - ν_{xy} ν_{yx}}

Formel 24

Gleichung 22:

D_{88} = d \cdot d_{33} \hat{=} G_{xy} d

Formel 25

Schubanteile:

Gleichung 23:

D_{44} = \frac{5}{6} G_{xz} \cdot d

Formel 26

Gleichung 24:

D_{55} = \frac{5}{6} G_{yz} \cdot d

Formel 27

Voraussetzung für diese Gleichungen ist natürlich immer, dass die Steifigkeitsmatrix positiv definit ist, also alle Eigenwerte der Matrix positiv sind.

Aus diesem Grund überprüft RFEM unter anderem die Definition der Querdehnung nach folgender Gleichung.

Gleichung 25:

ν_{xy} \leq 0, 999 \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formel 28

Beispiel

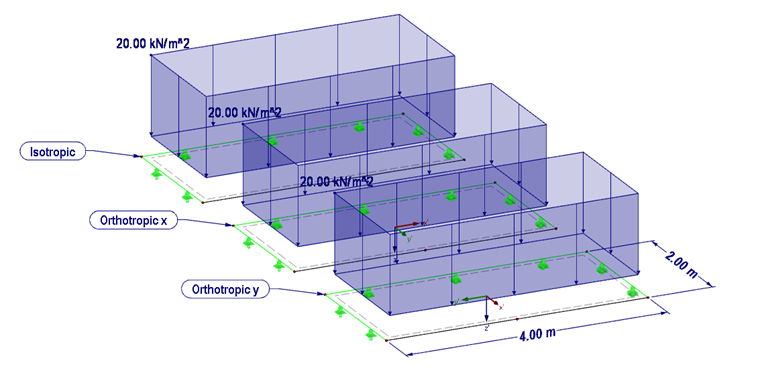
Mit folgendem Beispiel (Bild 03) wird das orthotrope Materialverhalten erläutert. Hierfür wird dem orthotropen Material ein isotropes Material gegenübergestellt. Zusätzlich wird die Steifigkeit der orthotropen Platte einmal mit der hohen Steifigkeit in x-Richtung und einmal in y-Richtung definiert.

System

System:

Plattendicke 200 mm
Material C24
Orthotrope Steifigkeiten

$\begin{array}{l} E_{x} = 1.100, 0 kN / {cm}^{2} \\ E_{y} = 37, 0 kN / {cm}^{2} \\ G_{y} = 6, 9 kN / {cm}^{2} \\ G_{x} = 69, 0 kN / {cm}^{2} \\ G_{xy} = 69, 0 kN / {cm}^{2} \\ ν_{xy} = 2, 52 \\ ν_{yx} = 0, 085 \end{array}$

Formel 29
Isotrope Steifigkeiten

$\begin{array}{l} E = 1.100 kN / {cm}^{2} \\ G = 500 kN / {cm}^{2} \\ ν = 0, 1 \end{array}$

Formel 30
Dimension b = 2,0 m, l = 4,0 m
Last 20 kN/m²
FE-Netzgröße 50 cm

Das System ist unverschieblich in vertikaler z-Richtung gelagert. Die Lagerbedingungen in x- und y-Richtung wurden so gewählt, dass keine Zwängungen entstehen.

Die Berechnung erfolgt nach Theorie I. Ordnung mit linear elastischem Materialverhalten und Lagerbedingungen.

Das hookesche Gesetz ergibt mit den gegebenen Werten folgende Querdehnung.

Gleichung 26:

ν = \frac{\sqrt{E_{x} \cdot E_{y}}}{2 \cdot G} - 1 = 6, 97

Formel 31

Diese hohe Querdehnung ist mit dem gewählten Materialmodel nicht möglich. Mit den Gleichungen aus [1] können die Werte jedoch angepasst werden.

Gleichung 27:

ν_{xy} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{x}}{E_{y}}}

Formel 32

Gleichung 28:

ν_{yx} \approx (\frac{\sqrt{E_{x} E_{y}}}{2 G_{xy}} - 1) \cdot \sqrt{\frac{E_{y}}{E_{x}}}

Formel 33

Gleichung 29:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{1.100}{37}} = 2, 52

Formel 34

Gleichung 30:

ν_{xy} = (\frac{\sqrt{1.100 \cdot 37}}{2 \cdot 69} - 1) \sqrt{\frac{37}{1.100}} = 0, 085

Formel 35

Flächen mit Steifigkeiten

Ergebnisse:
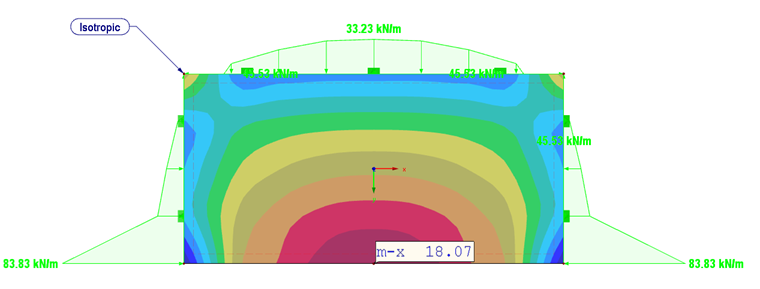
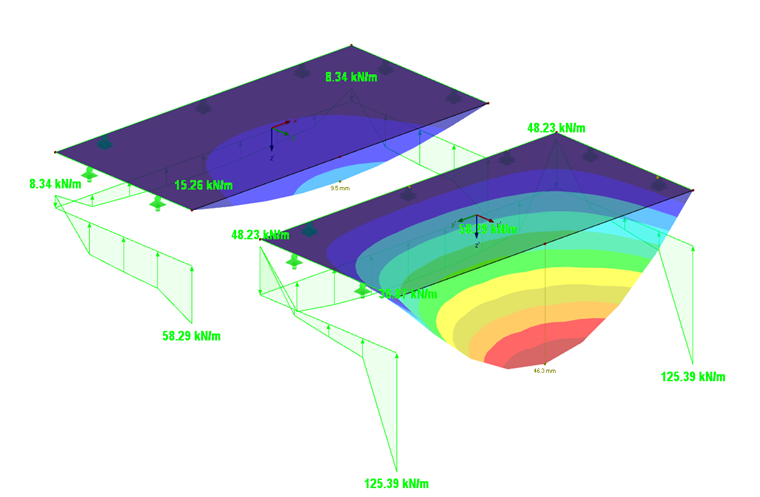
Wie zu erwarten, ergeben sich die größten Verformungen mit der Orientierung der Steifigkeiten in y-Richtung (Bild 06). Die Lagerreaktion und das Moment der isotropen Platte sind in Bild 05 dargestellt.

Ergebnisse isotropes Material

Da die Platte mit der hohen Steifigkeit in y-Richtung (E_y = 1.100 kN/cm²) die hohe Tragfähigkeit in dieser Richtung aufweist, sind dort auch die Lagerreaktionen höher (125,4 kNm zu 58,3 kNm).

Verformungen und Lagerreaktionen orthotroper Platten

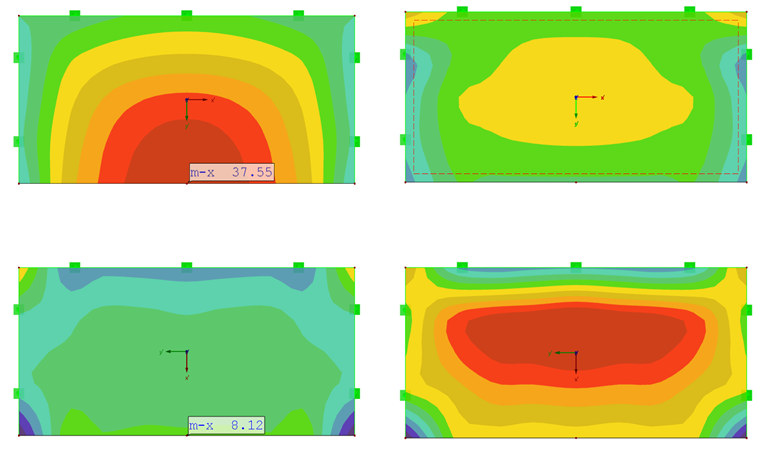
Die maximalen Biegemomente ergeben sich für die orthotropen Platten analog für m_x mit der Steifigkeit in x-Richtung und für m_y mit der hohen Steifigkeit in y-Richtung.

Für die Platte mit der hohen Steifigkeit in y-Richtung ist das maximale Biegemoment m_y nahezu in der Mitte der Platte (Bild 07).

Biegemomente der orthotropen Platte mx (links) und my (rechts)

Variation der Querdehnung

Die Querdehnung nach den Dehnungsbeziehungen kann, für ein Material der Festigkeit C24, die in der Tabelle aufgeführten maximalen und minimalen Werte erreichen.

	Max.	Min.
ν_xy	5,447	-5,447
ν_yx	0,183	-0,183

Die Eingangs eingeführte Platte mit der hohen Steifigkeit (E_x = 11.000) wird hierfür mit diesen hohen Querdehnungen definiert. Die anderen Steifigkeiten der Platte bleiben dabei jedoch unverändert.

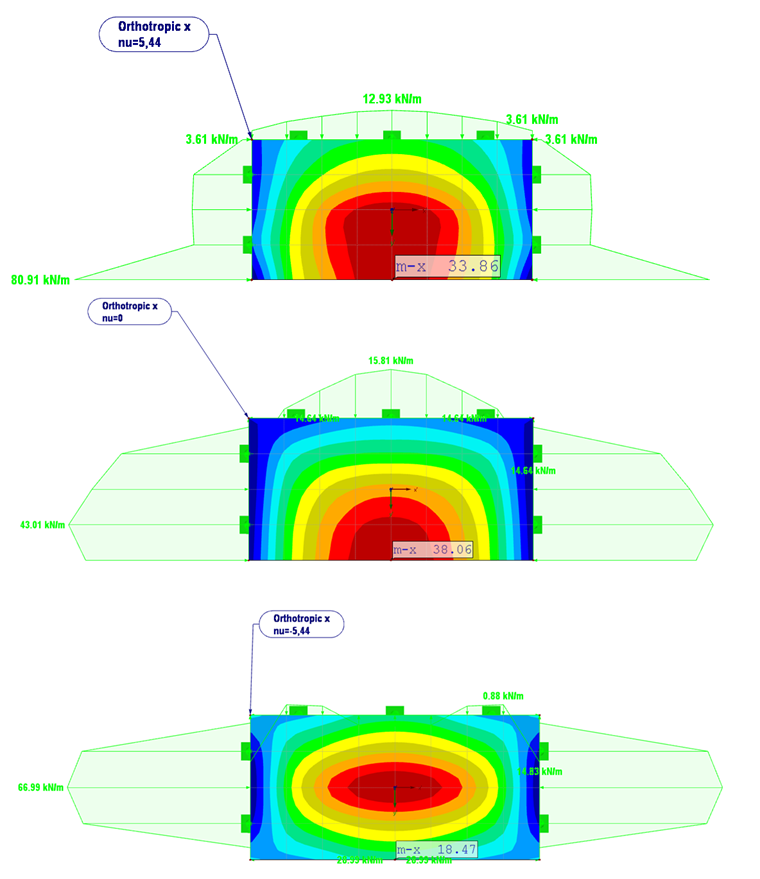
In Bild 08 sind die Ergebnisse der Variation von ν_xy = 5,44 bis -5,44 aufgeführt.

Für ν_xy = 5,44 sind die Lagerreaktionen qualitativ identisch zum isotropen Materialverhalten. Das Biegemoment vergrößert sich von m_x = 18,1 kNm/m (isotrope Platte) zu m_x = 34,9 kNm/m (orthotrope Platte).

Gegenüber der orthotropen Platte mit üblicheren Querdehnungen (ν_xy = 2,5) verkleinert sich das Biegemoment leicht.

Ergebnisse der Variation gemäß Tabelle (links: νxy = 5,44, Mitte: νxy = 0, rechts: νxy = -5,44)

Mit ν_xy = 0 verlagert sich der hohe Ausschlag der Lagerreaktion am freien Ende der Platte zu einem konstanten Wert von 43 kN/m.

Das Moment m_x vergrößert sich auf 38,1 kNm/m. Im Vergleich zum vorherigen Ergebnis (ν_xy =5,44) zeigt sich der Einfluss der Querdehnung. Für ν =0 wird keine Verformung oder Verzerrung aufgrund der Querdehnung hervorgerufen.

Für ν_xy = -5,44 ergibt sich ein Durchschlag am freien Plattenende und es werden die Lagerreaktionen negativ. Das maximale Moment ergibt sich in der Mitte der Platte mit 59,5 kNm/m.

Die Platte verhält sich jetzt mehr wie eine einaxial gespannte Platte, ohne das dritte Lager in seiner Längsrichtung.

Anhand Bild 01 und der dort aufgeführten Beziehungen lässt sich dieses Verhalten erklären.

Aufgrund der hohen negativen Querdehnung (ν_xy = -5,44) wird die Platte am freien Rand komplett überdrückt und kann sich daher hier nicht verformen.

Der Einfluss der Orthotropie in y-Richtung liegt hierbei nahe null (E_y ≈ 0).

Zusammenfassung

Mit dem orthotropen Materialmodell in RFEM ist eine nahezu beliebige Definition von Materialparametern möglich. Anhand der Variation der Querdehnungen können sehr unterschiedliche Ergebnisse erreicht werden. Eine Querdehnung nach Modifikation der Werte nach [1] ergibt Werte nahe der Lösung für einen Einfeldträger.

Gleichung 31:

M_{y} = \frac{q l^{2}}{8} = 40 kNm

Formel 36

Zu hohe negative Querdehnungen bilden ein geändertes statisches System ab, welches nicht mehr der Modellierung entspricht.

Autor

Herr Kuhn ist mit der Entwicklung und Qualitätssicherung im Bereich Holzbau betraut und im Kundensupport aktiv.

Links

Software für nichtlineare Berechnung

Referenzen

Huber, M. T.: The Theory of Crosswise Reinforced Ferroconcrete Slabs and Its Application to Various Important Constructional Problems Involving Rectangular Slabs, Der Bauingenieur 12, Seiten 354 - 360, und 13, Seiten 392 - 395. 1923

Downloads

;